
'항우는 어렸을 때 글을 배웠으나 다 마치지 못한 채 포기하고 검술을 배웠다. 이 또한 다 마치지 못했다. 항량이 노하자 항우는 말했다. "글은 이름과 성을 기록하는 것으로 족할 따름입니다. 검 또한 한 사람만을 대적할 뿐이니 깊이 배울만 하지 못합니다. 만인을 대적하는 일을 배우겠습니다." 항량이 병법을 가르치자 항우가 크게 기뻐했다. 그러나 대략 그 뜻만 알고는 또한 끝까지 배우려 하지는 않았다.'<사기본기 史記 本記 >(항우項羽 p317)
마지막 문장은 사마천(司馬遷, BC 145 ~ BC93)이 항우의 인물됨을 비판하기 위해 넣은 문장일 가능성이 큰 것이 사실이다. 그렇지만, 다른 한 편으로 항량이 항우가 원하는 것을 가르치지 못한 것은 아닐까하는 생각도 들게 된다. 만약, 항우가 만인(萬人)이라는 모호한 표현 대신 보다 구체적인 수치을 제시해서 뜻을 명확히 했다면 자신이 원하는 것을 배우지 않았을까. 수학(數學)은 구체적인 수치를 제시하여 통해 우리로 하여금 양(量)을 가늠케 한다. 이러한 수학의 위상은 서구 문명에서 더욱 크다.

'수학은 방법, 예술, 그리고 언어 이상의 것이다. 그것은 자연과학자와 사회과학자, 철학자, 논리학자 그리고 예술가들에게 도움이 되는 내용, 그리고 정치가와 신학자들의 교리에 영향을 주는 내용, 천체를 조사하는 사람들과 음악의 달콤함에 대하여 명상을 하는 사람들의 호기심을 만족시켜주는 내용, 그리고 비록 때로는 잘 지각되지는 않지만 현대 역사의 과정을 형성했음을 부인할 수 없는 내용으로 이루어진 지식의 총체이다.'(p24)
<수학, 문명을 지배하다 Mathematics in Western Culture>는 모리스 클라인(Morris Kline) 교수가 저술한 수학이 서구 문명에 미치는 영향에 관한 책이다. 음악, 미술, 물리, 경제 등 여러 분야와 수학이 어떤 관계를 맺고 있는가를 구체적으로, 그러나 어렵지 않게 서술하고 있다. 수학이 서구 문명에서 다른 분야와 어떤 관련이 있는가를 이번 페이퍼에서 구체적으로 살펴보자.
1. 미술 안의 수학 : 원근법
<수학, 문명을 지배하다>에서는 미술의 원근법에 대해 상세히 설명한다. '주 소멸점'이라고 불리는 한 점을 통해서 그림 감상자는 수직으로 그림과 만나게 되고, 주 소멸점을 중심으로 지평선이 뻗어가면서 구도를 잡게 된다. 또한, '주 소멸점'과 '대각선 소멸점' 사이의 관계 사이에도 원칙이 있는데, '등거리'와 '평행'의 원칙이 적용된다. 이러한 원칙하에서 실제와는 다소 차이가 있지만, 원근법을 통한 그림의 전체 구도가 잡히게 된다.
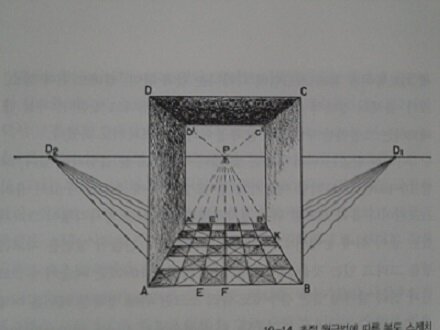
[그림] 원근법
'원근법의 수학적 주요 정리 또는 규칙은 무엇인가? 캔버스가 수직으로 놓여져 있다고 가정해보자. 눈에서 캔버스까지의 수직면은 주소멸점이라고 불리는 한 점에서 캔버스와 만난다. 주 소멸점을 통과하는 수평으로 된 선을 지평선이라 불린다. 그림에서 점P가 주 소멸점이며 선D2-P-D1이 지평선이 된다 ... 첫 번째로 핵심적인 정리는 그림 속에 있는 캔버스의 평면과 수직인 모든 지평선들은 주 소멸점과 만나도록 캔버스 위에 그려야 한다는 것이다. 그래서AA', EE', DD'와 다른 선들이 P에서 만나게 된 것이다...두 번째 정리는 AB'와 EK와 같은 선들은 실지 장면에서는 평행이며 캔버스의 면과는 45도의 각도로 점 D와 만나게 되는데, 이를 대각선 소멸점이라고 부른다. 여기서 거리 PD2는 거리 OP와의 거리, 즉 눈에서 주 소멸점까지의 거리와 같아야 한다... 세번째 정리는 캔버스 평면과 평행하는 장면의 평행 수평선들은 수평이면서 평행하게 그려야 하며 수직 평행선들은 수직이며 평행하게 그려야 한다는 것이다.'(p199)

[사진] 최후의 만찬( 출처 : https://brunch.co.kr/@bookfit/907)
주 소멸점이 눈에서 캔버스까지의 수직면이라는 정의를 생각해본다면 대표적인 원근법 적용 작품으로 알고 있는 <최후의 만찬>을 우리는 현장에서 제대로 감상하지 못한다는 사실을 알 수있다. 아래에서부터 올려다 보는 관점은 원근법의 수학적 원칙을 위반한 감상관점이 아닌지 생각하게 된다.
2. 음악 안의 수학 : 푸리에 변환

'장 바티스트 조제프 푸리에 남작(jean Baptiste Joseph, Baron de Fourier, 1768 ~ 1830)은 물체를 가열했을 때의 열의 전달 방식을 연구하고 있었다. 그는 열이 퍼져 나가는 상태도 파동으로 나타낼 수 있었다. 푸리에가 관찰한 파동은 매우 복잡했지만 주기를 갖고 있었다. 즉, 같은 형태의 파동이 거듭하여 나타나는 것이었다. 같은 형태를 반복하는 주기를 가진 파동은, 아무리 복잡한 것이라도 단순한 파동이 결합해 이루어진다.'<수학으로 배우는 파동의 법칙>(p24)
<수학으로 배우는 파동의 법칙>은 푸리에 법칙에 대해 그림과 함께 설명했기 때문에 푸리에 급수에 대해 보다 이해를 쉽게 한다. 주기를 가진 파동은 단순한 파동의 결합이라는 푸리에 법칙이 음악에는 구체적으로 어떻게 적용될 수 있을까?
'순수 수학의 정리라고 말하기에는 푸리에의 공헌이 너무나 단순한 것처럼 보인다. 그 정리에 따르면, 주기적인 음을 나타내는 공식은 a sin bx 형식에서 단순한 sin 항들의 총합이다. 게다가 a sin bx의 형태로 나타난 간단한 사인 항들의 빈도는 두 배, 세 배처럼 가장 낮은 것의 정수 곱으로 나타난다.(p413)... 그렇다면 푸리에의 정리는 물리학적으로 어떠한 중요성을 지니고 있는가? 수학적 언어로 보면, 이 정리는 어떤 음향의 공식이든 모두 a sin bx의 형태로 된 항들의 합이라는 것을 보여준다. 이 항들은 각각 적절한 진동과 진폭을 지닌 소리굽쇠의 소리와 마찬가지로 단순 음향을 나타내기 때문에, 이 정리에 따르면 아무리 복잡한 음향이라도 모든 음향은 소리굽쇠가 내는 소리인 단순 음향들의 결합으로 나타낼 수 있다는 것이다.'(p414)
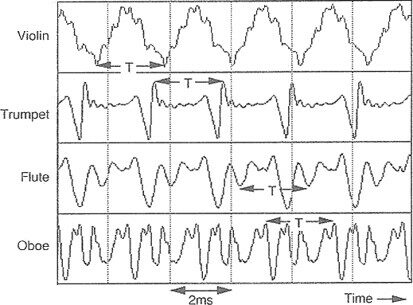
[그림] 악기와 푸리에 변환(출처 : http://fluorf.net/lectures/lectures3_2.htm)
악기로 연주할 수 있는 음(音)은 옥타브(octave : 주파수가 두 배 차이 나는 두 음 사이의 음정)으로 세분화할 수 있다. 이는 음을 sin과 cos함수로 분석할 수 있으며, 이는 음악을 수학적으로 표현할 수 있다는 것을 의미한다. 이는 음악과 AI(artificial intelligence)이 결합할 경우 '예술적 영감(靈感)'없이도 작곡이 될 수 있다는 것을 의미하기도 한다. 한편, 음사이의 수학적 관계는 피타고라스(Pythagoras, BC 582 ? ~ BC 497 ?)가 최초로 제시하였으며, 바흐(Johann Sebastian Bach, 1685 ~ 1750)에 의해 동일하게 조율된 음계가 제기된 이후 서양의 기본 음계로 자리잡게 되었다.
'피타고라스의 발견에 따르면, 가장 듣기 좋은 코드, 즉 화음은 그 진동수가 단순 정수들의 비율이 되는 소리들로 구성된다. 예를 들어 장음 3도는 그 진동수의 비가 4대 5인 한 쌍의 음, 즉 음정이 된다. 4도는 그 진동수가 3 대 4인 음정이며, 5도는 2 대 3인 음정이다. 이들 화음이 우리 귀에 즐겁게 들리는 것은 화음의 고저 사이에 이와 같은 산술 관계를 인식하는 것으로 잘 설명된다... 각 음의 진동수가 고정되어 있는 피아노와 같은 악기들로부터 무한한 또는 아주 넓은 범위의 진동수를 창출하는 것이 불가능하기 때문에 동일하게 조율한 음계를 구성함으로써 그러한 어려움을 해결하였다. 바흐와 그의 아들 카를 필립 에마누엘이 이 음계를 주창하였으며, 이후 서구 문명은 이를 영구히 채택하기에 이른다.'(p420)
동일하게 조율된 음계(평균율 平均律, Equal temperament)는 완전한 협화를 포기하고 모든 음의 간격을 동일하게 만든 음계를 말한다. 이러한 평균율을 사용하여 만든 대표적인 곡이 바흐의 <평균율 클라비어(Well-Tempered Clavier)>다.
'동일하게 조율된 음계에는 12개의 음이 있다. C에서 한 옥타브 높은 C'까지는 12개의 음정이 있게 된다. 11개의 중간 음들의 진동은 고정되어 있으며 각 음들은 앞선 음과 일정한 비율을 가진다. C에서 C' 사이에 12개의 음정이 있고, 이 두 음의 진동 비율은 2이기 때문에 연속한 음들의 진동 비율은 (1.0594의 12승 = 2) 1.0594이다. 그러므로 반음으로 불리는 동일하게 조율된 음계에서 각 음정은 동일하다. 결과적으로 어떤 음이든 작곡할 때 조로 사용될 수 있다.'(p420)
20세기에 들어 12음계를 사용한 기법은 아르놀트 쇤베르크(Arnold Schoenberg, 1874 ~ 1951)에 의해 더욱 발전하게 된다. 12음계의 수학적 의미는 다음과 같이 정리될 수 있다.

'음악의 패턴들, 특히 음의 높낮이와 리듬은 수학적으로 잘 설명할 수 있었고, 그중 일부는 대수적 논리로 다룰 수 있었다. 특히 12개의 똑같은 평균율의 음표체계는 자연스럽게 모듈러 연산을 이용하여 모형화되었고, 이는 조합론 명제들과 함께 20세기 음악이론에 사용되었다.(p439)... 아르놀트 쇤베르크(Arnold Schoenberg)의 12음계 작곡 기법은 1920년대 시작되었는데, 12음계 음악에서는 12음계를 똑같은 중요성을 가진다고 가정한다. 특히 장조나 단조에서 으뜸음처럼 특별한 위치를 차지하는 단음이 없다. 12음계 곡의 기본 요소는 음렬(tone row)로 반음계의 12음의 어떤 치환에 의해 주어진 수열이다. 일단 음렬이 선택되면, 네 가지 유형의 변환, 즉 조옮김, 전위, 역행, 역행, 역행전위에 의해 조작될 수 있다. 음악의 조옮김은 수학에서 평행이동에 해당한다.'<The Princeton companion to Mathematics>2(p445)
3. 경제 속의 수학 : 상관관계
데카르트(Rene Descartes, 1596 ~ 1650)과 페르마(Pierre de Fermat, 1601 ~ 1665)는 현재 우리가 사용하고 있는 사분면과 방정식을 결합시키는 아이디어를 고안한다. 이는 기하학과 대수학이 결합하게 된 계기가 되었는데, 이 아이디어는 '일대일대응 一對一對應'에 기반한 수학적 사고다.
'데카르트와 페르마가 행한 아이디어의 핵심은 명백하다. 각 곡선에는 다른 점이 아닌, 그 곡선의 점만을 유일하게 나타내는 하나의 등식이 존재한다. 역으로 x, y와 관련된 각 등식은 x와 y를 점의 좌표로 해석함으로써 곡선으로 나타낼 수 있다. 공식화 하여 말하면, 어떤 곡석은 등신은 다른 점들의 좌표에 의해서가 아니라, 그 곡선상의 모든 점들의 좌표에 의하여 만족되는 대수식과 동일하다. 이제 등식과 곡선의 관련이 바로 새로운 사고의 핵심이다. 대수의 최선과 기하학의 최선을 결합함으로써, 데카르트와 페르마는 기하학적 도형을 연구하는 새롭고, 엄청나게 가치있는 방법을 가지게 된 것이었다.'(p244)
'일대일대응 一對一對應'의 관계가 유지되는 자연법칙과는 달리 사회과학 속에서는 '일대다대응 一對多對應'의 관계가 성립되어 일반적인 공식을 유도하기 어렵다. 이러한 경우 수학적으로 '상관관계(Correlation Analysis)'를 분석하게 된다. 그리고, 상관관계 분석은 폭넓은 자료의 활용을 가능케하여 사회과학 발전에 이바지한다.
'골턴(Francis Galton, 1822 ~ 1911)은 상관관계라는 개념을 도입했다. 두 변수간의 상관관계는 둘 사이의 관계를 측정한 것이다. 이 측정치, 혹은 수치는 -1에서 +1까지의 값을 갖는 특별히 고안된 상관계수를 말한다. 1의 상관이 있으면 이것은 정적인 관계가 있다는 것을 나타낸다. -1의 상관이 있다는 말은 한 변수가 정확히 다른 변수가 변화하는 것과 반대로 변화하는 것을 뜻한다.(p490)... 상관관계라는 개념은 광범위하게 사용될 수 있다. 가령, 미국의 산업 생산 수준을 연구하기 위해서는 복잡한 자료를 수집하는 일이 필요하다. 그러나, 만일 산업 생산과 주식거래소에서 거래되는 주식의 수량 사이에 높은 상관 관계가 있다면, 그 중에서 더 쉽게 얻을 수 있는 자료, 즉 주식의 수량을 이용할 수 있다.'(p491)
4. 물리 속의 수학 : 상대성 이론
현대 물리학은 수학없이는 성립하지 않는다. 현대 물리학에서 가장 대표적인 아인슈타인(Albert Einstein, 1879 ~ 1955)은 그의 '상대성 이론 (theory of relativity)'을 적절한 함수의 선택을 통해 훌륭하게 증명했음을 이 책을 통해 확인할 수 있다.
'행성의 위치는 네 개의 좌표를 사용함으로써 구체화된다는 것에 주목해보자. 네 개의 좌표 중 세 개는 공간 속의 위치에 해당하는 것이며, 나머지 하나는 그 위치를 사건이 점유하게 되는 시간을 뜻한다. 연속적인 위치는 4차원 수학적 세계의 곡선상에 놓여 있다. 아인슈타인이 각 행성의 "경로"가 그 결과로 형성된 기하학에서 최단 거리를 나타내는 선이 되도록 공간-시간차에 대한 공식을 선택했다는 데에 그의 위대함이 있는 것이다.'(p607)
'산맥 속에 있는 산들의 형태 차이가 지구 표면상의 최단 거리를 나타내는 선을 다양하게 만들어내듯이, 공간-시간 간격에 대한 공식 속에 적절한 함수를 선택함으로써, 아인슈타인은 물리적 세계의 질량의 존재가 그 질량 주변의 공간-시간과 최단 거리를 나타내는 선의 성격을 결정하도록 자신의 공간-시간을 만들었던 것이다. 지구 표면 근처의 물체들은 이 지역의 공간-시간의 최단 거리를 나타내는 선을 따르는 것뿐이므로, 그 경로를 설명하는 데에 만유인력 같은 것은 전혀 필요 없게 된다.'(p608)

<상대성 이론>에서 각 행성의 경로가 최단 거리를 나타낸다는 선이 되도록 아인슈타인이 설명했으나, 현대 양자 이론에서는 행성의 경로(빛의 경로)가 확률적으로 결정됨을 설명한다. 이와 관련하여 파인만(Richard Phillips Feynman, 1918 ~ 1988)의 <일반인을 위한 파인만의 QED강의>를 참고해도 좋을 것 같다.
이처럼 <수학, 문명을 지배하다>에는 수학이 서구 문명에 미치는 영향에 대해 쉽지만, 구체적으로 살펴보고 있어 흥미롭게 읽을 수 있는 책이다. 다만, 영문 제목과 다른 제목 번역은 책 내용과는 다소 떨어진 느낌이 들어 아쉽다. 또한, 수학자인 저자의 한계일까. 수학이 발달하지 못한 로마 문명은 창조적인 문명이 아니라 빌려온 문명이라는 저자의 비판은 쉽게 공감하기 힘들다.
'경영과 관리 및 정복에 모든 힘을 쏟아부었고, 아름다운 아치 밑을 통과하는 군대의 개선 행진으로만 상징되는 것은 아니겠지만, 어쨌든 둔감한 사람의 상징으로 묘사되는 로마인들은 실용적인 정신의 소유자였다. 그러나 이들은 진정으로 창조적이고 독창적인 것을 거의 만들어내지 못했다. 간단히 말해 로마 문화는 빌려온 것들이다. 로마의 통치 시기에 이루어진 대부분의 업적들은 모두 로마의 정치적 지배를 받고 있던 소아시아의 그리스인들이 이룬 것이기 때문이다.'(p28)
다소 공감하기 어려운 부분도 있지만, <수학, 문명을 지배하다>속에서 우리는 수학이 서구 문명의 근원이었음을 우리는 확인하게 된다. 서구 문명에 대한 수학의 이러한 공헌에도 불구하고, 지나친 추상화를 통한 관념(觀念)화와 동떨어진 이론화는 우리가 경계해야할 부분이라고 여겨진다. 마지막으로, <수학, 문명을 지배하다>를 읽으며 떠오른 우화하나를 옮겨본다.
'수학의 추상적 정리들과 그것들을 적용하는 것과의 관련에 대하여 또 다른 점을 짚고 넘어가야 한다. 추상적 정리들은 이상적인 경우를 진술하는 것인 반면에, 그것이 적용되는 물질적 상황은 이상과는 거리가 멀다는 것을 염두에 두는 것이 매우 중요하다는 사실이다.'(p84)

'어떤 사람이 황금 알을 낳는 예쁜 암탉 한 마리를 갖고 있었다. 그는 암탉의 몸속에 금덩이가 들어있는 줄 알고 암탉을 죽였다. 그러나 그 암탉은 여느 암탉과 똑같았다. 그는 단번에 부자가 되려다가 가지고 있던 작은 이익마저 잃고 말았다.'<이솝 우화> 황금알을 낳는 암탉 (p313)
원래 위의 우화는 지금 가지고 있는 것에 만족하라는 의미를 가지고 있지만, <수학, 문명을 지배하다>를 읽으면서 조금은 다른 관점에서 생각하게 된다. 달걀을 낳는 닭도, 황금을 낳는 닭도 결국 같은 닭이었던 것처럼 음악, 미술등의 예술, 사회과학, 자연과학 등의 서구 문명에서의 여러 분야가 '수학'이라는 하나의 원리로 수렴되는 것은 아닌가하는 다소 엉뚱한 생각을 하며 이번 페이퍼를 마친다.