-

-
오일러가 사랑한 수 e ㅣ 경문수학산책
엘리 마오 지음, 허민 옮김 / 경문사(경문북스) / 2020년 8월
평점 : 


지수 함수와 삼각 함수 사이의 놀라운 관계에 대한 발견은 예상치 못한 다른 관계들의 등장을 거의 피할 수 없게 만들었다. 오일러는 x=pi를 이용해서 다음의 공식을 얻었다... 이 공식은 분명히 수학 전체에서 가장 아름다운 공식의 하나에 속할 것이다. _ 엘리 마오, <오일러가 사랑한 수 e>, p244
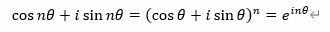
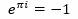


엘리 마오 (Eli Maor)의 <오일러가 사랑한 수 e, e : The Story of a Number>는 자연로그의 밑 e에 대한 역사를 소개한다. 세상에서 가장 아름다운 공식이라는 오일러공식(Euler's formula). 오일러는 자신의 공식에 특수한 경우 x=pi이라는 특수한 상황을 통해 간결하면서도 아름다운 등식을 유도한다. 사실 의미는 부여하기에 따라 달라지기는 하지만, 무리수 이면서 초월수와 허수를 지수함수 형태로 표현한 결과가 0과 1로 떨어진다는 것은 수학을 잘 모르는 이들에게도 경이롭게 보여지는 것이 사실이다.

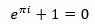


이것을 다시 쓰면, 수학에서 가장 중요한 다섯 개의 상수를 연결하는 공식을 얻는다. 그리고 수학에서 가장 중요한 세 가지 연산인 덧셈, 곱셈, 지수도 얻는다. 이 다섯 개의 상수는 고전 수학을 대표하는 네 가지 주요한 분야를 상징적으로 나타낸다. 즉, 0과 1은 산술을, i는 대수학을, pi는 기하학을, e는 해석학을 각각 나타낸다. _ 엘리 마오, <오일러가 사랑한 수 e>, p245
<오일러가 사랑한 수 e>에서는 네이피어(John Napier of Merchiston, 1550~1617)에 의해 로그가 만들어진 후, 복리계산의 극한값으로서 e가 갖는 의미를 여러 각도에서 조망한다. 뉴턴(Sir Isaac Newton, 1642~1726)과 라이프니츠(Gottfried Wilhelm Leibniz, 1646~1716)에 의해 적분의 개념이 도출되면서 pi와 e는 각각 원과 쌍곡선의 넓이로 해석되었고 이들의 유사성에 대한 관심은 결국 오일러의 등식을 통해 이들을 하나의 수식으로 결합시켰음을 확인하게 된다.
네이피어는 로그를 만들 때 한 세기 뒤에 로그의 보편적인 밑으로 인정받았고 수학에서 pi(파이) 다음으로 중요한 역할을 하는 수의 발견에 부지불식간에 매우 가까이 접근했었다. 그 수 e는 n의 값이 무한대로 커질 때 (1+1/n)^n의 극한값이다. _ 엘리 마오, <오일러가 사랑한 수 e>, p13
원 함수 사이에서 성립하는 모든 관계에 대응하는 쌍곡선 함수 사이의 관계가 존재하기를 희망할 것이다. 그러면 원 함수와 쌍곡선 함수를 완전히 똑같은 기초 위에 세울 수 있고, 이에 따라 쌍곡선에 원과 똑같은 지위를 부여할 수 있을 것이다. 불행하게도, 이렇게 할 수 없다. 쌍곡선과 달리, 원은 폐곡선으로, 이를 따라 돌아가면 모든 것은 원래의 상태로 되돌아간다. 필연적으로, 원 함수는 '주기적'이다. 즉, 함수 값이 2pi마다 반복된다. _ 엘리 마오, <오일러가 사랑한 수 e>, p222
오일러의 공식에서 x=pi로 입력할 경우 cos과 sin 값이 간결하게 나오기 때문에, 오일러는 이를 활용했는지도 모르겠다. 그렇지만, 이러한 오일러의 간결한 시도 뒤에는 폐곡선인 원과 개방곡선인 쌍곡선을 로그 소용돌이선의 주기성이라는 공통분모로 pi와 e를 하나의 공식으로 통합하는 오일러의 날카로운 통찰이 있었음을 본문 내용을 통해 새삼 깨닫게 된다. 본문의 모든 내용을 다 이해하기에는 부족함이 있었지만, 비전공자들도 수학의 아름다움에 대해 다시 생각하는 계기를 주는 좋은 책이라 여겨진다...
pi(파이)는 단위원의 넓이로 해석되는 반면에, e는 쌍곡선 아래의 넓이를 1로 만드는 x축상의 선분의 길이이다. 수학에서 가장 유명한 두 수의 이런 유사한 역할은 이 둘 사이에 어쩌면 더 심오한 관계가 있을 것이라고 추측하게 한다. _ 엘리 마오, <오일러가 사랑한 수 e>, p162
로그 소용돌이선의 가장 두드러진 성질 몇 가지는 함수 e^X의 도함수가 자기 자신과 같다는 사실에 기인한다. 예를 들면, "극을 지나는 모든 직선은 로그 소용돌이선과 똑같은 각도로 교차한다." 게다가, 로그 소용돌이선은 이런 성질을 가진 유일한 곡선이다. 그래서 로그 소용돌이선을 '등각 소용돌이선'이라고 부르기도 한다. 이런 성질 때문에 로그 소용돌이선은 원과 밀접한 관계가 있는데, 원은 극을 지나는 모든 직선과 90도로 만난다. 사실, 원은 증가율이 0인 로그 소용돌이선이다. _ 엘리 마오, <오일러가 사랑한 수 e>, p187
네이피어가 생각한 방향은 다음과 같다. 만약 임의의 양수를 어떤 고정된 수(나중에 ‘밑‘이라 부름)의 거듭제곱으로 쓸 수 있다면, "수들의 곱셈과 나눗셈은 그 수들의 지수의 덧셈과 뺄셈과 일치한다." 게다가 어떤 수의 n제곱, 즉 그 수를 n번 거듭 곱한 값은 지수를 n번 거듭 더한 것, 즉 지수에 n을 곱한 것과 일치한다. 그리고 어떤 수의 n제곱근은 n번 거듭 뺀 것, 즉 n으로 나눈 것과 일치한다. 요약하면, 각 산술 연산은 연산 체계에서 그보다 쉬운 연산으로 환원됨으로써, 수치 계산의 어려움을 엄청나게 감소시켜 준다. - P9
복소수 영역으로 함수의 확장은 실수 영역에서의 모든 성질을 보존할 뿐만 아니라, 함수에 새로운 특징을 실제로 부여한다. 함수론에서 가장 멋진 정리 중 하나는 f(z)가 해석적인(미분 가능한) 각 점에서 이 함수는 ‘등각 사상‘이라는, 즉 각을 보존한다는 정리이다. 등각 사상이란, z-평면에 있는 두 곡선에 각도 b로 교차하면, w-평면에 있는 그것들의 상인 곡선들도 각도 b로 교차함을 의미한다. - P274
|