‘세상에 바뀌지 않는 사실은 ˝세상 모든 것은 바뀐다˝는 사실이다.‘

튜링 & 괴델 : 추상적 사유의 위대한 힘 ㅣ 지식인마을 36
박정일 지음 / 김영사 / 2010년 11월

<튜링 & 괴델>은 튜링의 '보편 튜링 기계'와 괴델의 '불완전성 정리'의 개념을 중심으로 현대 수학의 집합론과 컴퓨터에 대해 설명한 수리논리학 입문서다. 

<튜링 & 괴델>에서는 두 수학자의 이론이 다루어진다.

영화 <이미테이션 게임 Imitation game>으로 유명한 튜링(Alan Mathison Turing, 1912 ~ 1954)의 '보편 튜링 기계'를 설명하기 위해 <튜링 & 괴델>에서는  프레게(Friedrich Ludwig Gottlob Frege, 1848 ~ 1925)의 <개념 표기법 Begriffsschrift>(1879)상의 '문장 논리'와 '술어 논리', 칸토어(Georg Ferdinand Ludwig Philipp Cantor, 1845 ~ 1918)의 '집합론'의 개념을 연관설명하고 있다. 또한, 괴델(Kurt Godel, 1906 ~ 1978)의 '불완정성 정리'를 설명하기 위해 힐베르트(David Hilbert, 1862 ~ 1943)의 '힐베르트 프로그램'의 개념을 소개한다. 

프레게는 기존 아리스토텔레스(Aristoteles, BC 384 ~ 322)의 삼단논법으로 대표되는 기존 논리학 대신 문장연결사를 활용한 '현대 논리학'을 창시했으며, 현대 논리학과 무한(infinty)의 개념을 잠재무한(potential infinity)과 실제무한(actual infinity)으로 구분한 칸토어의 '무한론'은 튜링기계(Turing machine)의 이론적 토대가 된다. 책에서는 튜링 기계의 작동원리가 후대 컴퓨터 특히 인공지능(AI)과 어떤 방식으로 연결될 수 있는지가 '보편 튜링 기계(universal Turing Machine)'를 통해 설명된다.

'간단히 말하면 보편 튜링 기계란 다른 튜링 기계가 할 수 있는 모든 일을 흉내낼 수 있는 기계를 말한다(p108)... 그렇다면 보편 튜링 기계가 의미하는 바는 무엇인가? 보편 튜링 기계에서는 다른 튜링 기계의 프로그램이 하나의 수치로, 다시 말해 하나의 데이터로 입력되고 처리된다'(p123)

[그림] 알파고 서버(출처 : http://www.insight.co.kr/newsRead.php?ArtNo=54225)

괴델의 불완전성 정리는 '제1불완전성 정리'와 '제2불완전성 정리'로 나눌 수 있다.

'수학의 체계가 무모순이라면, 수학의 체계에서는 참이지만 증명할 수 없는 명제가 존재한다는 것이다(제1불완전성 정리). 나아가 수학의 체계가 무모순이라면, 수학의 체계에서 모순이 도출되지 않는다는 것을 그 체계에서는 증명할 수 없다는 것이다.(제2불완전성 정리)' (p161)

'한 문장에 대해서 그 자신과 그것의 부정이 동시에 증명 불가능한 경우, 그 문장을 결정 불가능한 문장이라고 부르며, 이를 "괴델의 제1불완전성 정리"이다.'(p167).. 괴델은 산수 체계의 무모순성이 그 체계 내부에서 증명될 수 없다는 것을 증명했다.'(p180)

<튜링 & 괴델>에서는 각각의 명령어가 어떤 방식으로 개별 숫자에 대응할 수 있는지를 보여주고, 이러한 수대응(數對應)이 무한히 계속될 수 있음을 통해, 보편 튜링 기계의 작동이 '멈추지 않는다'는 것을 보여주고 있다. 그리고, 이러한 개념은 '기계는 생각할 수 있는가?'의 문제제기로 이어진다. 책에서 제기한 이러한 질문에 대해 2015년 알파고와 이세돌의 바둑 게임 결과로 답을 할 수 있다고 생각된다. '기계학습'을 통해 발전하는 인공지능(AI)의 시대를 살아가는 우리에게 <튜링 & 괴델>은 컴퓨터의 기본개념에 대해 잘 설명해주는 좋은 입문서라 생각된다.

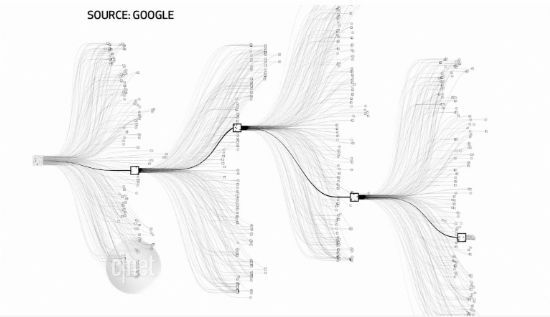
[그림] 바둑의 경우의 수( 출처 : http://www.bloter.net/archives/249668)

이러한 입문서로서의 역할 이외에도 <튜링 & 괴델>은 수리논리학이 결코 <수학 정석>의 집합, 명제 수준이 아님과 수학의 여러 정리를 추가적으로 제시하여 독자의 흥미를 더한다. 그 중 두 가지를  소개해본다.

1. 부랄리-포르티 역설과 안셀무스의 신 존재 증명

<튜링 & 괴델>에서는 칸토어의 역설을 설명하면서 '부랄리-포르티 역설'을 설명하고 있는데, 이는 중세 안셀무스의 신 존재 증명을 연상시킨다. 서양에서 무한(infinity)라는 개념은 신(God)의 존재와 뗄 수 없는 관계라는 생각이 든다.

[부랄리-포르티 역설]

모든 서수들의 집합은 존재하는가? 다시 말해 가장 큰 서수는 존재하는가? 이를 증명하기 위해 가상의 집합 Ω를 가정하자. 이 집합에는 0, 1, 2, 3, ... ω(초한 서수)가 포함될 것이다. 모든 서수들의 집합 Ω의 서수는 Ω의 원소인 어떤 서수보다 크며, 가장 큰 서수가 될 것이다. 그런데 Ω로부터 Ω+1을 구성할 수 있다. 또한 Ω+1은 Ω보다 더 크다. 그러나 이는 가 가장 큰 서수라는 사실과 모순된다.(p142)

[안셀무스의 신 존재 증명] 

1. 신은 그보다 더 큰 것이 상상될 수 없는 존재다.(가장 큰 존재다.)

2. 이런 신의 개념은 인간의 지성 속에 존재한다. (즉, 그런 개념을 인간이 이해할 수 있다.)

3. 신이 실재가 아닌 마음 속에만 존재한다고 가정하자.

4. 그것은 마음 속에 한정된 신보다 더 큰 개념이므로, 그보다 더 큰 것이 상상될 수 없는 존재라는 신의 정의에 모순된다.

5. 따라서 신은 실제로 존재한다. (출처 : 위키피디아)

2. 러셀의 역설(Russell's paradox)

책에서는 자기 지시의 모순의 대표적 예로 러셀의 역설을 소개한다.

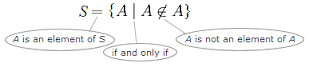
[그림] 러셀의 역설( 출처 : 네이버)

S라는 집합을 "자신을 원소로 포함하지 않는 모든 집합들의 집합"으로 정의하자. 다시 말해, A가 S의 원소가 되기 위한 필요충분조건은 A가 A의 원소가 아닌 것으로 한다. 이 경우 "S는 S의 원소이다"라는 명제와 "S는 S의 원소가 아니다"라는 명제는 둘 다 모순을 도출하여 맞다 혹은 그르다 중에 어떤 답으로 답할 수 없다. (출처 : 위키피디아)

러셀의 역설을 이용해서 한 가지 명제를 만들어 보면서 리뷰를 마치고자 한다.

'세상에 바뀌지 않는 사실은 "세상 모든 것은 바뀐다"는 사실이다.'

PS. '분명하게 말할 수 있는 것은 "모든 것을 분명하게 말할 수는 없다."라는 사실이다' 라는 명제 때문에 비트겐슈타인(Ludwig Josef Johann Wittgenstein, 1889 ~ 1951)것이 '말할 수 없는 것에 대해 침묵해야한다'고 한 것은 아닐테지...