원주율(pi)의 역사 : 인류의 역사

π의 역사 ㅣ 경문수학산책 17
페트르 베크만 지음, 박영훈 옮김 / 경문사(경문북스) / 2002년 1월

지금도 그렇지만 대학생 때 나는 시(詩)에 대해 잘 알지 못했었다. 그런 내가 어느날 교보문고에서 본 어느 시집 제목이 상당히 인상적이었다.

<손끝으로 원을 그려봐 네가 그릴 수 있는 한 크게 그걸 뺀 만큼 널 사랑해>

한때 150만부나 팔린 원태연 시집 제목이다. 당시, 이 시집 제목을 보고 "이 사람 선수구나." 라는 생각을 했었다. 이와 같은 고백을 듣고 가슴설레지 않을 사람이 있을까.(물론 이런 표현은 가끔 써야지 자주 들으면 별로 효과도 없을 것이다.)

'세상에서 너를 가장 사랑해'라는  이 멋진 말을 수학적으로 따져보면 다음과 같이 나오지 않을까. 

한국여성의 평균 키가 162.3cm라 가정(2014년 평균)했을 때, 두 팔을 뻗었을 때의 근사치는 160cm다.  원의 정의를 고려할 경우 이 여성이 그릴 수 있는 원의 크기는 약 509.6cm수준으로 계산된다. 이 원을 제외한 세상의 크기는 무한대에 가깝다. 결국 '무한대 - 509.6cm'만큼 너를 사랑한다는 이야기가 성립하며, 수학에서 말하는 무한대의 극한을 고려하면, '무한대-509.6cm'는 무한대로 수렴한다...

* 유클리드 기하학에서 원(圓) 또는 동그라미는 평면 상의 어떤 점에서 거리가 일정한 점들의 집합으로 정의되는 평면도형이다(출처 : 위키피디아)

** 원주율(圓周率)은 원의 지름에 대한 둘레의 비율을 나타내는 수학 상수이다. 수학과 물리학의 여러 분야에 두루 쓰인다. 그리스 문자 π로 표기하고, 파이(π)라고 읽는다

결국, '네가 어떻게 해도, 난 너를 무한히 사랑해.'라는 다소 억지스럽고 무리한 수학적 해석을 해본다.  위의 전개 논리중 162.3cm에서 509.6cm으로 가는 과정, 즉 원주율(파이)의 역사를 다룬 책이 <파이의 역사 A History of pi>다.

파이의 역사에서는 원주율을 중심으로 수학의 역사를 설명한다. 원주율을 구하는 방법을 크게 기하학적인 방법, 대수학적인 방법, 확률론적인 방법으로 구분하여 각각의 역사를 기술하고 있는데 기본적인 내용과 결론을 요약하면 다음과 같다.

기하학적으로 원주율을 구하려는 노력은 아르키메데스의 방법이 가장 대표적이다. 원에 내접하는 도형의 길이를 구해면서 근사값을 산출하는 방법으로 현대적으로는 삼각함수와 소수점을 활용한 방법이다. (p80)

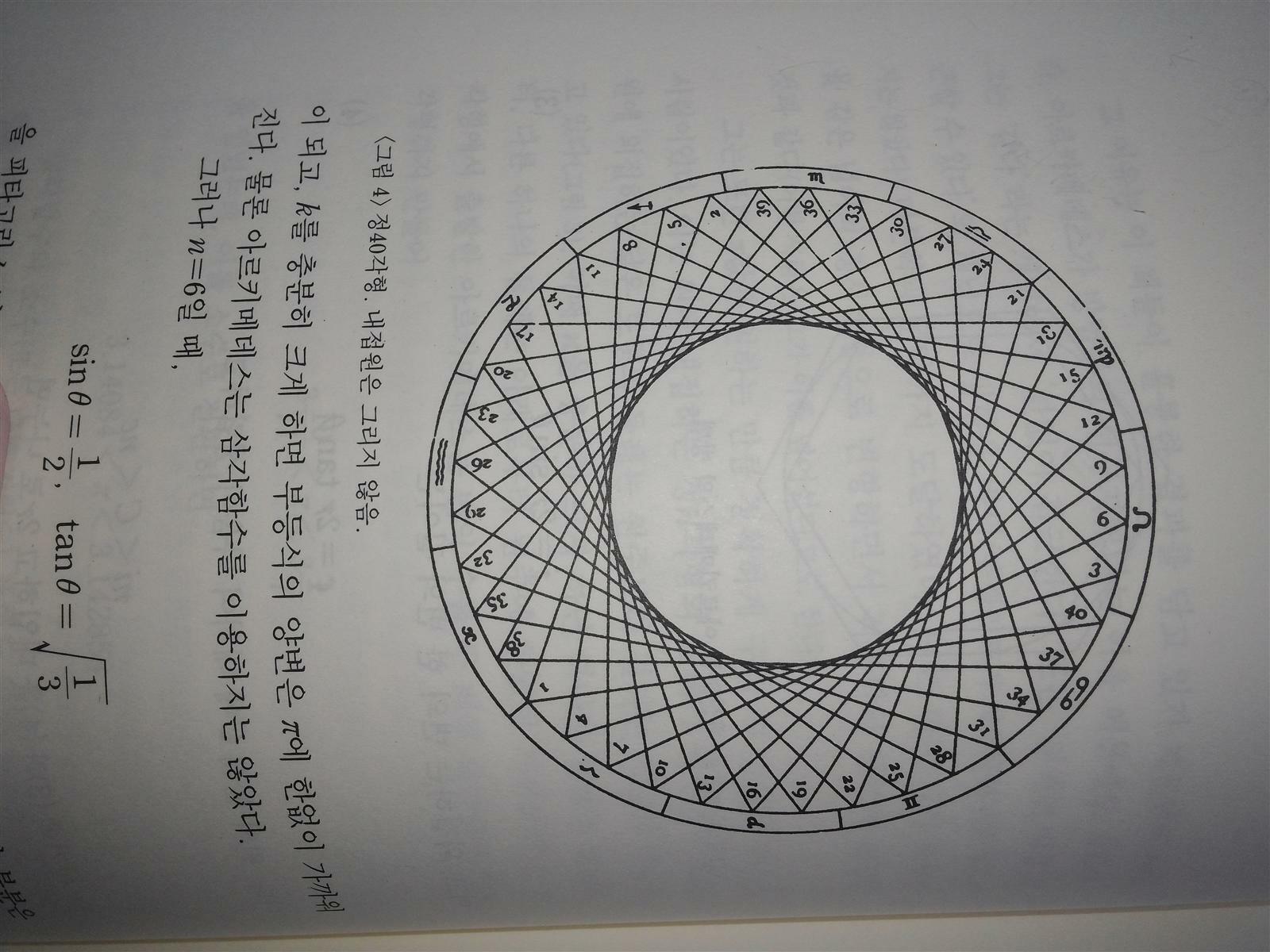
대수학적으로 원주율을 구하려는 방법은 미적분학과 극한의 개념을 사용하는 방법이다. 여러 방법 중 특히 라이프니츠(1646~1716)에 의해 '라이프니츠 급수'라는 방법으로 새로운 방법론이 제시된다.(p172)

원주율(pi) = 4(1-1/3+1/5-1/7+....)

그러나, 라이프니츠 급수는 원주율에 수렴하는 정도가 너무 늦었기 때문에, 뉴튼과 오일러 등 여러 수학자들에 의해 새로운 방법이 계속 발견되었다. 특히 오일러는 arctan의 방법을 사용하여 pi의 수치 계산에 종지부를 찍게 된다.(p202)

원주율(pi) = 20arctan1/7+ 8 arctan3/79

원주율이 초월수(transcendental : 무리수도 아니면서 대수 방정식의 근도 되지 않는 수)라는 사실이 1882년 린데만에 의해 밝혀지면서, 원주율 계산에 확률론적인 방법이 도입된다. 라플라스(1749~1827)에 의해 계산된 방법은 다음과 같다.

원주율(pi) = 2L/dP

바늘의 길이 L과 선분들 사이 길이 d가 주어졌을 때(일반적으로 L=d), 바늘과 선분이 만날 확률은 충분히 많은 횟수만큼 바늘을 종이 위에 던져 바늘이 선분 위에 놓이는 횟수를 기록하여 정하는 방법이다. (p213)

이러한, 라플라스의 방법은 컴퓨터의 발전과 더불어 빛을 발하는데, 대표적인 방법 중 하나가 경영분석 방법으로도 알려져 있는  '몬테카를로 방법'이다. 원주율 계산은 컴퓨터의 발전과 더불어 초월수이면서 비순환소수인 원주율(pi)의 자리수는 계속 발견되고 있다.

이 책에서는 이처럼 수학의 여러 분야에서 '원주율'이라는 주제를 어떻게 풀이하고 있는가를 설명하고 있다. 이를 통해 각 분야의 수학사(數學史)와 더불어 기본 원리에 대해서도 알려주고 있다. 또한, 유클리드의 <원론>에 관한 설명부터, 제논의 역설(아킬레스와 거북이의 경주)이 역설이 아닌 이유에 이르기까지 여러 수학 분야에 대한 이야기를 다루기 때문에 흥미있게 읽을 수 있는 책이다.

유클리드의 <원론>에서 5가지 공리에 대한 이야기를 하면서 가장 문제가 되는 5번째 공리없이도 유클리드가 증명한 내용은 성립한다. 때문에, 반드시 5번째 공리가 성립할 필요가 없으며, 오히려 5번째 공리의 붕괴를 통해 '비(非)유클리드 기하학'이 성립되는 과정을 흥미롭게 설명한다. (p62)

거북이가 아킬레스보다 10미터 앞에서 출발하는 경주에서 아킬레스가 10미터를 가는 동안 거북이는 1미터를 가고, 다시 아킬레스가 1미터 가는 동안 거북이는 1/10미터를 가는 과정에서 결국 아킬레스는 영원히 거북이를 잡을 수가 없다는 제논의 역설에 대한 본서의 설명은 다음과 같다.

'여기에서 걸림돌은 그리스인들이 유한 값에 이르는 무한개의 합을 생각할 수 없었다는 것이다. (p56)'

<파이의 역사>를 읽으면서 기하학과 대수학이 다루는 대상이 다를지라도, 비순환소수인 원주율(pi)을 산출하는 방법은 동일하다는 것을 알 수 있었다. 그것은 일종의 '오류법'으로 파이(pi)로 다가가기 위한 포기하지 않는 노력이라 생각된다. 수작업으로 하기에 고통스러웠던 계산과정이었지만, 포기하지 않는 노력은 결국 컴퓨터의 발전을 통해 그 빛을 보게 되었다는 생각이 든다. (2010년 현재 구한 pi자리수는 2조 7천억 자리라고 한다.)

그러한 의미에서  원주율(pi)를 구하는 과정은 인간의 역사의 대표적 단면이라는 생각을 하게 된다.

PS. <손끝으로 원을 그려봐 네가 그릴 수 있는 한 크게 그걸 뺀 만큼 널 사랑해>에서 화자(話者)의 의도를 청자(聽者)가 안다면, 그 감동의 크기가 줄어들 것이라는 생각이 든다. 이 상황을 소비자의 완전정보하에서의 상황과 불완전정보의 상황과 연계시켜서 생각해보는 것도 재밌을 것 같다.^^: