-

-
일반인을 위한 파인만의 QED 강의
리처드 파인만 지음, 박병철 옮김 / 승산 / 2001년 8월
평점 :



'빛과 물질의 상호작용을 양자역학적으로 설명하는 이론이 일단의 물리학자들에 의해 1929년 빛을 보게 되었으며, 거기에는 "양자전기역학"이라는 끔찍한 이름이 붙여졌다.'(p27)
<일반인을 위한 파인만의 QED 강의>는 제목 그대로 양자전기역학(QED ; Quantum Electrodynamics)을 일반인들이 이해하기 쉽게 설명한 책이다. 파인만(Richard P. Feynman, 1918 ~ 1988) 은 어려운 수학 대신 이 책에서는 기초적인 확률법칙과 '화살표'를 이용하여 어려운 개념을 설명하고 있다.
그렇다면, 이 책 <일반인을 위한 파인만의 QED 강의>에서 설명하고자 하는 개념은 무엇일까? 전체 4강(講)으로 구성된 본문에서 이 개념을 설명하고 있다.
'폴 디랙 Paul Dirac은 그의 이론을 통하여 전자가 자기능률 magnetic moment(작은 자석에 의한 힘과 비슷한 개념)을 갖고 있으며 그 세기는 특정한 단위를 썼을 때 정확하게 1이 되어야한다고 주장하였다... 줄리안 슈위거 Julian.S. Schwinger는 "야바위 놀음 shell-game"을 사용하여 처음으로 올바른 자기능률값을 계산해냈다. 그 결과는 1.0116이었는데 이것은 실험치와 매우 비슷한 값이었으므로 우리의 계산법이 옳다는 사실을 입증한 셈이었다. 내가 여러분에게 앞으로 설명하게 될 이론이 바로 이것이다.'(p29)
1. 빛은 입자다
파인만이 설명하는 '빛 Light'은 눈에 보이는 빛만을 의미하지 않는다. 우리는 일반적으로 빛이 파동운동을 하는 것으로 알고 있는데 이러한 고정관념을 버릴 것을 파인만은 요청한다.
'내가 말하는 빛이란, 적색에서 파란색에 걸쳐 있는 가시광선만을 뜻하는 게 아니다. 가시광선은 빛의 일부분에 지나지 않는다... 자외선, 적오선, TV파, 라디오파등으로 옮겨간다. 이 모든 것들이 다 "빛"이다...눈에 보이는 것만이 실재라면 물리학은 당장 와해된다.'(p39)
'나는 빛이 입자처럼 행동한다는 점을 여러분에게 강조하는 바이다. 이것을 머리속에 새겨두기 바란다. 특히 학교에서 "빛은 파동처럼 행동한다."고 배웠던 사람들에게 강조한다. 다시 한 번 말하건대 빛은 정말로 입자처럼 행동하고 있다.'(p41)
2. 빛은 어떤 경로로 움직이는가?

[그림2] p43
전등에서 나온 빛이 유리판에서 반사되어 일부가 감지기에 도달하는 실험을 통해 파인만은 부분반사의 개념에 대해 의문을 제기한다. 특히 이러한 부분 반사 현상은 유리판 양면(윗면과 아랫면)에서 이러한 현상을 관찰했을 때 더 극명하게 발견하게 된다.
가. 부분반사
'실험 결과, 광원에서 곧장 90도 아래 유리판으로 향한 100개의 광자 중에서 평균적으로 4개가 A에 도달하고 96개는 유리표면을 통과하여 B에 도달한다는 사실이 알려졌다. 즉, 이경우에 4%의 광자만이 반사되고 나머지 96%는 유리를 투과한다는 것을 뜻한다. 어떻게 입사된 빛의 일부만이 반사된다는 말인가? 개개의 광자는 A로 갈 수도 있고 B로 갈 수도 있다. 광자는 자신의 갈 길을 어떻게 결정하는가?'(p44)

[그림4] p47
빛의 부분반사 문제를 해결하기 위해 파인만은 '화살표'를 활용한다. 본문에서 화살표의 길이와 방향은 확률의 크기와 빛의 방향성을 의미한다.
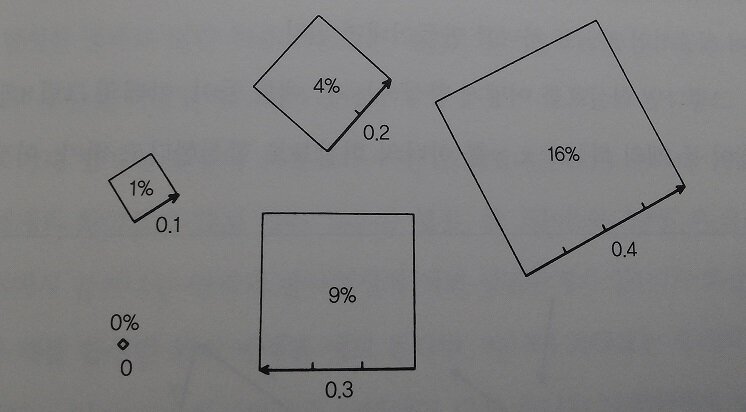
[그림6] 유리판의 양면에서 일어나는 부분반사현상을 설명하려면, 하나의 사건이 일어날 확률만을 알아내는데 만족해야 한다. 그리고 이 확률은 양자전기역학을 이용하여 계산할 수 있다. 화살표 하나를 그려서, 그로부터 만들어지는 정사각형의 면적이 곧 확률이 된다.(p53)
'어떤 특정한 사건이 일어날 확률과 화살표 사이에는 어떤 관계가 있는가? 사건이 일어날 확률은 화살표의 길이의 제곱과 같다.'(p52)
화살표의 합성 법칙은 다음과 같이 '기본법칙'과 '일반법칙'으로 구분할 수 있다.
'1) 기본법칙 : 하나의 사건이 일어날 확률은 "확률진폭 Probability amplitude"이라 불리는 화살표의 길이의 제곱과 같다. 예를 들어 길이가 0.4인 화살표는 0.16 또는 16%의 확률을 나타낸다.
2) 일반법칙 : 하나의 사건이 일어날 수 있는 방법이 여러 가지 있을 때에는 각각에 대해 화살표를 그린 후 화살표의 머리를 다른 화살표의 꼬리에 갖다 붙임으로써 이들을 합성(덧셈)하여 최종 화살표(첫번째 화살표 꼬리에서 마지막 화살표 머리를 이어준 화살표)를 그린다.(갖다 붙이는 순서에는 무관하다.) 이렇게 만들어진 최종 화살표의 길이를 제곱한 값이 곧 사건이 일어날 전체 확률을 나타낸다.'(p71)
'어느 특정한 사건이 일어날 확률은 합성된 최종 화살표 길이의 제곱과 같다. 그리고 최종 화살표는 그 사건이 일어날 수 있는 모든 가능한 경우의 화살표들을 합성하여(또는 더하여) 얻어진다.'(p74)
<일반인을 위한 파인만의 QED 강의>에 있어 가장 중요한 내용은 [그림24]로 생각된다. 이 내용을 기초로 하여 파인만은 빛의 이중성, 빛의 산란, 빛의 투과 현상을 설명하는데, 중요한 내용은 다음 그림에서 대부분 설명된다.
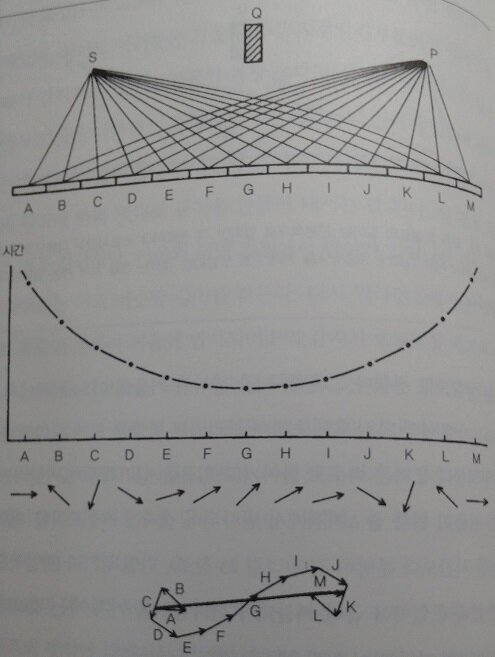
[그림24] 빛이 거울에서 반사되어 감지기에 도달하는 모든 가능한 경로들이 그림의 상단부에표시되어 있다. 중앙부의 그림은 각 경로에 소요되는 시간을 세로축에 표시한 그래프이다. 그래프 아래에 그려진 화살표는 각 경로에 해당되는 화살표의 방향을 나타내며, 가장 하단에는 이 모든 화살표들을 합성한 최종 화살표가 굵은 선으로 표시되어 있다. 최종 화살표의 길이는 주로 E에서 I 사이의 화살표에 의해 생긴다. 왜냐하면 그 사이에 있는 경로들은 길이가 서로 비슷하여 화살표의 방향도 서로 엇비슷하기 때문이다. 그리고 이 지점은 소요시간이 가장 적은 편에 속하는 경로들이 밀집되어 있는 지역이므로, 빛이 최단 시간 경로를 따라서 진행한다고 말해도 크게 틀리지 않는다.(p78)
[그림24]를 통해서 파인만은 빛이 입자처럼 운동하고 있으며, 빛은 무한히 많은 경로를 통해 운동하고 있으나. 확률에 따라 실제 우리에게 관측되는 빛의 운동은 최단경로를 따라 진행된다는 것을 설명하고 있다.
결국 <일반인을 위한 파인만의 QED 강의>에서 파인만은 '빛이 한 점에서 다른 점으로 가는데 직진만 하는 것이 아니라 가능한 모든 길을 동시에 지나간다'는 사실을 기초로 하여 '전자 자체는 희미하게 퍼져 있는 안개같은 존재이나 빛으로 관측할 때는 뚜렷한 점으로 보인다'는 사실을 우리에게 설명하고 있다.
본 리뷰에서 직접 다루지 않았지만, 간섭현상등을 설명하는 3장, 4장에서는 확률의 덧셈법칙과 곱셈법칙을 이용하여 내용을 설명하고 있다. 책에서 활용되는 확률의 두 법칙은 아래와 같다.
[확률의 두 가지 합성법칙 rule of composition]
'1) 덧셈법칙 : 한 사건이 여러 가지의 독립적 경로를 통하여 발생 가능한 경우에는 각 경로를 지나갈 확률을 모두 더한다.
2) 곱셈법칙 : 한 사건이 순차적인 여러 단계를 거쳐 발생하는 경우에는 각 단계의 확률을 모두 곱한다.'(p128)
<일반인을 위한 파인만의 QED강의>는 최소한의 수학(확률의 법칙)과 화살표를 활용하여 양자전기역학(QED)의 핵심(核心)을 잘 설명하고 있다. 그럼에도 양자물리학의 세계가 워낙 어렵기 때문에, 우리와 같은 일반인들이 이해하기는 쉽지 않은 것도 사실이다. 이 책의 모든 내용을 이해하기위해 노력하기보다 양자물리학의 세계가 확정성의 세계가 아닌 '불확정성의 세계'라는 것을 이해하고, '열린 가능성'을 우리가 진정으로 깨달을 수 있다면 그것으로 이 책의 목적은 달성한 것이 아닐까하는 생각을 해본다.