본 논문에선 '삼차각'이 상대론의 주 배경인 4차원 공간상에서 물체의 물리적 위치를 초구면좌표계로 나타날 때 필요한 세 개의 각도값임을, 그리고 '육면각'이 삼차각의 적분으로 얻어지는 초입체각인 동시에 4차원상에서 한 점에서 만나는 여섯 개의 면이 이루는 각임을 주장할 것이다. 이는 신범순이 '삼차각'에 대해 "더 높은 차원"을 지향하는 공간기호학적 기호"라 지적한 것과 상통하는 바이며, 또한 앞서 언급한 권희철의 아이디어, 즉 "육면각체"가 한 꼭지점마다 여섯 개의 면이 만나는 4차원 초입방체'라는 아이디어와 일부 궤를 같이한다. 마지막으로 <삼차각설계도 - 각서1>과 <건축무한 육면각체 - AU MAGASIN DE NOUVEAUTES>에 나타난 차원 확장에 대해 탐구할 것이다. _ 오상현 외, <이상 시의 4차원 시공간 설계 및 건축>, p111
얼마 전 서재 이웃인 mini74님의 글 중에서 이상(李箱, 1910~1937)의 시(詩) <건축무한육면각체>의 일부 내용에 대한 비밀이 밝혀졌다는 흥미로운 기사를 읽었다. 개인적으로도 다른 이상의 작품 안에서 아인슈타인(Albert Einstein, 1879~1955)의 상대성이론의 내용이 담겨있다는 책을 읽었던 적이 있기에 더 관심이 갔는지도 모르겠다.
이상의 <운동>에 담긴 상대성 이론 관련 페이퍼 : https://blog.aladin.co.kr/winter_tiger/9364036#Comment_9364036
바로 논문을 찾아 읽고 싶었지만, 때마침 프로젝트 완료일이 맞물려 며칠이 지난 후에 겨우 논문을 읽을 수 있었고, 페이퍼를 통해 해당 내용을 정리한다.
사실, <삼차각설계도> <건축무한육면각체>를 다룬 선행 연구가 없었던 것은 아니다. 개인적으로 소장하고 있는 이상 전집에도 작품에 담긴 차원(次元)의 문제에 대해 해설되고, 차원 확장의 가능성에 대해서도 짧게나마 분명하게 언급된다. 물리/수학적 해석이라는 점에서는 동일하지만, 기존연구(권영민)에서는 더 깊이 들어가지는 않는다. 또한, <삼차각설계도>와 <건축무한육면각체> 두 연작시 내에서는 관련성을 찾지만, 전체적으로는 별개의 작품으로 해석되고 있다.



이 작품의 큰 제목은 '삼차각설계도'로 표시되어 있으며, <조선과 건축>(1931,10)에 김해경(金海卿)이라는 본명으로 발표된 <선에관한각서 1-7>이라는 일곱 편의 작품이 묶인, 일종의 연작시로서의 성격을 지닌다. 이 작품들은 모두 수학적 또는 물리학적 개념이 중심을 이루고 있으며, 우주 공간, 태양과 광선, 과학과 시간 등에 관한 새로운 지식들을 동원하여 인간의 존재에 관한 다양한 상념을 해체시켜 기표화한 것이 특징이다. _ 권영민, <이상 전집 1> , p272
이 방법(데카르트 좌표계)은 유클리드 기하학의 내용을 더욱 풍부하게 하였고, 또한 3차원에서 일반적인 n차원으로의 확장을 가능하게 한다. 이 같은 해석기하학의 원리는 뒤에 기하 도형의 평면적 2차원적 위상을 입체적이고 공간적인 3차원에서 다룰 수 있는 다양한 대수 기하학의 원리로 발전하게 된 것이다. _ 권영민, <이상 텍스트 연구>, p103
이에 대해 오상현은 이번 연구를 통해 물리학자의 입장에서 시를 접근하면서 <삼차각설계도>와 <건축무한육면각체>라는 각각의 연작시들을 통합하고 있다. 차별화된 접근법은 '삼차각'이라는 용어에서부터 드러난다. 기존 연구에서는 '삼차각'을 3차원에서 용어를 정의하려 했기에 부정확한 용어의 사용으로 해석해왔다.
연작시의 내용과 의미를 이해해보기 위해 가장 먼저 선행 되어야 하는 작업 중 하나는 시에 드러난 물리학적 개념과 용어들에 대해 온전히 파악하는 것이라 할 수 있을 것이다. 특히, 연작시의 제목에 나타난 용어인 "삼차각"과 "육각면체" 등이 정확히 무엇을 의미하는지를 이해하는 것은 연작시 전반에의 이해에 큰 도움이 될 것이 분명할 것이다. _ 오상현 외, <이상 시의 4차원 시공간 설계 및 건축>, p109
여기서 제목으로 내세운 '삼차각설계도'라는 말 가운데 '삼차각'은 수학 용어로서는 부정확한 말이다. 수학에서 말하는 '각(角)'이라는 것은 3차원 이상의 공간에서도 언제나 2차원 평면에서의 '각'이라는 개념으로 규정된다. 그러므로 '삼차각'이란 수학적 개념이라 말하기 어렵다. 다만 세 모서리가 만나는 각을 말하는 것으로 본다면 그 존재를 인정할 수 있다. _ 권영민, <이상 전집 1> , p272
반면, 오상현의 연구에서는 이를 4차원에서 삼차각을 정의하는 발상의 전환을 보여준다. 그리고, 이를 위한 근거를 이어지는 <선에관한각서 2>에서 찾는다. 1+3을 1개의 시간과 3개의 공간으로 해석하며 자신의 논증을 뒷받침한다.
선에관한각서 2
1+3
3+1
3+1 1+3
1+3 3+1
1+3 1+3
3+1 3+1
3+1
1+3... (중략)
이제까지의 논의를 통해, 삼차각이 4차원 공간에서의 3차원 각도값이라 해석하는 것이 자연스러운 수학적 개념의 연장선상에 있음을 보였다. 이를 고려할 때, '삼차각설계도'의 의미는 4차원 공간상에서의 설계도로 해석된다. 이때 이상이 설계한 4차원 공간이란, 1개의 시간축과 3개의 공간축이 결합된 4차원 시공간이라 보는 것이 타당하다. _ 오상현 외, <이상 시의 4차원 시공간 설계 및 건축>, p116
논문에서 저자는 '삼차각'이 4차원 공간에서의 3차원 각도값으로 정의한 후 두 연작시의 관계를 설계-건축의 프로세스로 정의한다. <삼차각설계도>가 4차원 상의 설계라면, <건축무한육면각체>는 그것의 건축과정이라는 결론을 끌어낸다.
설계와 건축이라는 행위가 긴밀하게 연결된다는 점, 그리고 <삼차각설계도> 발표 1년 후 <건축무한육면각체>가 발표됐다는 점을 떠올려 보면, <삼차각설계도>에서 설계한 대상은 '무한육면각체'이며, <건축무한육면각체>는 그것을 건축하는 과정으로 해석하는 것이 자연스럽다. _ 오상현 외, <이상 시의 4차원 시공간 설계 및 건축>, p117
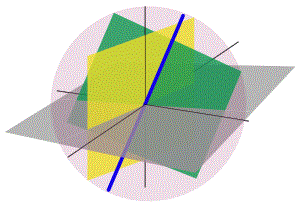
다만, 결론을 보기에 앞서 우리는 먼저 다중선형사상(multilinear map) 또는 텐서(tensor), 벡터(vector)를 먼저 알아두는 편이 좋을 듯하다. 벡터, 텐서를 통한 차원 확장의 이해는 <건축무한육면각체>에서 사각형 중심 결합을 통한 차원 확장과도 연관되기 때문이다.
차원확장은 어떻게 이루어지는가. 오상현은 '사각의중의사각의중의사각의중의사각'이라는 시구에 주목한다. 삼차각의 크기는 사차원에서 최소 6개의 면이 만나 정의되는데, 시구에서는 '사각'이 4번 반복된다는 것이다. '사각 중의 사각'(편의상 띄어쓰기함)을 사각형의 중심결합으로 4번 반복을 하지만, 4번째 반복을 마지막으로 중심결합을 중단하면서 4차원 이상 고차원인 5/6차원으로의 도약을 허용하지 않는다는 해석을 내리며, 이상 시의 배경이 4차원으로 한정됨을 논증한다.
[그림] 벡터공간(출처 : 위키백과)


민코프스키는 허수의 시간 변수를 도입하여 4차원 연속체에서의 불변량이론을 3차원 유클리드공간 연속체에서의 불변량이론과 아주 닮은 형태로 만들었다. 따라서 특수상대성이론의 4차원 텐서이론은 3차원 공간의 텐서이론과 비교할 때 실수성과 차원의 수에서만 다르다... 성분들 가운데 첨자에 4가 한 번 들어간 것들은 순허수이고, 이것들을 제외한 나머지는 모두 실수이다. 3차 이상의 고차텐서들도 비슷한 방법으로 정의할 수 있다. 또한 이것들을 제외한 나머지는 모두 실수이다. 3차원 이상의 고차텐서들도 비슷한 방법으로 정의할 수 있다. _아인슈타인, <상대성이란 무엇인가> , p96
정리하면, '삼면각체'란 3차원에서의 임의의 각진 도형을 말하는 것이다. 또한, n-삼면각체란 n개의 점을 가진 3차원에서의 임의의 각진 도형을 의미함을 확인할 수 있다. 동일한 논리로, 무한-삼면각체란 3차원에서 무한한 점을 가진 삼면각체이며, 3차원상의 (각질 수도, 매끈할 수도 있는) 임의의 도형을 말함을 알 수 있다.(p123)... 3차원에서는 최소 세 개의 면이 만나 이차각 크기가 정의 되어 그것이 '삼면각'이라 불리듯이, 4차원에서는 최소 6개의 면이 만나 삼차각 크기가 정의되며, 자연스럽게 그것을 '육면각'이라 부를 수 있기 때문이다. _ 오상현 외, <이상 시의 4차원 시공간 설계 및 건축>, p125
(<건축무한육면각체>의 "사각의중의사각의중의사각의중의사각"은 무엇일까? 3차원상에서는 더이상 xy-xz-yz 사각형 결합체의 중심에 또 다른 사각형의 중심을 온전히 결합할 수 없다. 때문에 새로운 축, 즉 4차원의 축(w축)을 도입하여야하며, 여기서 논의영역이 3차원에서 4차원으로 확장된다.(p145)... 이상은 4개 평면(xy, xz, yz, xw)의 사각형 중심 결합은 활용하지 않았다. 즉, 시에서 논의하는 공간을 4차원으로 확장시키자마자 사각형 중심 결합이라는 도구의 활용을 중단하였다. _ 오상현 외, <이상 시의 4차원 시공간 설계 및 건축>, p146



이러한 논의 끝에 내려진 저자는 논문에서 다음과 같이 결론내린다. 마치 3D프린터에서 출력물들이 시간의 흐름에 따라 쌓이는 모습(stacking prints)처럼 작가 이상은 자신이 작품에 표현하고자 하는 것을 담고자 하지만, 차원의 한계를 넘지 못하는 것에서 느끼는 절망과 대안이 두 작품에 표현되었다는 것이 논문의 내용이다. 그 절망은 결핵에 걸린 환자 이상, 식민지 지식으로서의 한계를 넘지 못하는 작가 이상의 한계에서 오는 것일수도 있겠지만, 시간(time)을 넘지 못하는 인간 본연의 절망이기도 할 것이다. 빛 조차도 광속(光速)이상의 속도를 내지 못하기에 시간을 되돌릴 수 없다는 1930년대의 '현재'에서 그가 느낀 절망은 오늘날 우리 모두에게 주어진 공통된 것이 아닐까.
결과적으로, '육면각체'란 4차원에서의 임의의 각진 도형을 말하는 것이며, '무한육면각체'란 4차원에서의 임의의 도형을 말하는 것이라는 결론에 이를 것이다. 이러한 해석을 인정할 경우, 이상이 언급한 '무한육면각체'란 4차원 시공간에서의 임의의 도형(즉, 3차원 물체의 시간에 따른 움직임을 4차원 시공간에서 본 것)을 말하는 것이며, '삼차각설계도'와 '건축무한육면각체'의 의미는 3차원 물체의 시간에 따른 변화까지 4차원 시공간에서 설계하고 건축함이라 볼 수 있다. _ 오상현 외, <이상 시의 4차원 시공간 설계 및 건축>, p120
건축가는 3차원 물체를 설계하고 건축하지만, 3차원 공간에 직접 설계를 진행할 수는 없다(절망). 대신 2차원 도면에 설계를 진행하고, 거기에 3차원 정보를 담기 위해 여러 투상도와 정보를 기입하여 2차원 도면의 한계를 극복한다. _ 오상현 외, <이상 시의 4차원 시공간 설계 및 건축>, p128
이처럼 오상현의 이번 연구는 육면각체가 일반적인 인식차원인 3차원이 아닌 4차원에서의 개념이라는 용어정의를 통해 개별 연작시로 받아들여지던 <삼차각설계도>와 <건축무한육면각체>가 실은 긴밀한 연관성을 갖는다는 사실을 입증했다는 점에서 주목을 받는다. 논문의 내용은 여기까지이지만, 이상 연구에 있어 이들 작품 뿐 아니라 그의 작품(또는 삶) 전체가 연계성을 가질 수도 있다는 가능성을 제시했다는 점과 그의 난해한 시가 실은 치밀하게 설계된 의도적인 작품임을 밝혔다는 점에서 분명 뜻깊은 논문이라 생각된다.
이상의 연작시 <선에 관한 각서 1~7>은 모든 사물에 대한 인식의 주체가 인간이라는 점, 그리고 사물에 대한 인식이라는 것이 결국은 시각에 의한 것임을 강조하면서 그 시상의 결말에 도달한다(p120)... 이상은 먼저 인간의 감각 가운데 시각은 빛과 밀접한 관련을 가지며 삶의 모든 과정이 빛을 통한 시각에서 이루어진다는 점을 강조한다. 그리고 사물에 대한 인식도 시각을 통해 이루어지며, 모든 사물의 존재를 드러내는 이름이라는 것이 결국 시각의 표현이라는 점에 주목하고 있는 것이다. _ 권영민, <이상 텍스트 연구>, p121
이번 이상관련 논문을 읽으면서 개인적으로 '피라미드 설계자' 이상을 생각하게 된다. 파라오의 무덤을 도굴꾼으로부터 지키기 위해 피라미드 내부를 복잡하게 설계한 이들. 그들처럼 작가 이상 역시 자신의 내면 깊은 생각을 곳곳에 숨겨놓은 암호처럼 숨겨 놓은 것은 아닐런지. 그의 삶이 채 30년이 안 된 짧은 시기였지만, 한문(漢文) 파자(破字)에 능하고 많은 작품이 일본어로 씌여졌으며, 공학적 지식이 담긴 작품이 많기에 접근하기에 쉽지는 않지만, 드물게 '가슴'이 아닌 '머리'를 노래한 시인 이상의 매력은 90년의 시간이 흐른 후에도 결코 사라지지 않음을 확인한다. 마지막으로, 재밌는 주제를 던져주신 미니님께 감사드리며 페이퍼를 갈무리한다...




ps. 논문원문을 보고 싶은 분들을 위해 KCI 논문 URL을 첨부한다. 본문에서 보다 충실한 저자의 설명을 만날 수 있을 것이다.
https://www.kci.go.kr/kciportal/ci/sereArticleSearch/ciSereArtiView.kci?sereArticleSearchBean.artiId=ART002754263