-

-
이상한 수학책 - 그림으로 이해하는 일상 속 수학 개념들
벤 올린 지음, 김성훈 옮김 / 북라이프 / 2020년 3월
평점 :



조카는 수학자가 되고 싶다고 했다.
뭐라고? 수학자?
천재 수학자들의 생애라거나 에피소드를 읽는 건 재미있지만 그들이 연구한 수학의 내용에 대해 이해하는 건 정말 재미없는 내게 수학자, 가 되고 싶다는 꿈은 정말 위대하거나 무모하거나.. 라는 생각을 하게 된다.
누구나 한번쯤은 피타고라스의 정리 증명을 배우고 실제 증명을 하는 재미에 맛들이기도 하지만 그렇다고 누구나 수학을 재미있게 생각하게 되지는 않을 것이다. 당시 수학선생님은 열정이 넘치는 분이셨는데 주말에 집에서 무료한 시간을 보내다가 마라톤 대회하는 장면을 보게 되었는데 마라톤 선수들은 백미터를 몇초에 뛰는걸까, 라는 궁금증에 앉아서 그 계산을 하셨고 그때 내게 남은 기억은 마라톤 선수가 뛰는 백미터의 기록이 내 백미터 기록과 맞먹는 수준이라는 것 뿐이기는 했지만 수학이라는 것을 실생활에 써먹는다는 개념을 처음으로 갖게 되었던 기억이기도 하다.
아무튼 그렇게 숫자로만 알고 있는 수학이라는 것이 또 다르게 다가왔던 것은 빗방울에 대한 이야기때문이었던가? 숫자만이 수학이라고 알고 있던 내게 수학은 일상생활에서 볼 수 있는 많은 것들의 규칙성을 찾거나 배열을 찾아내는 학문이기도 하다는 것을 느끼게 해 줬다. 그런 느낌이 남아있어서 그런지 '이상한 수학책'은 머리아프게 하는 어려운 학문이 아니라 우리에게 친근하게 느낄 수 있게 하는 수학을 알려주는 책일 것이라는 생각을 갖고 읽기 시작할 수 있었다.
어떤 학문이든 '개념'이 중요한 것인데 이 책을 차근차근 읽다보면 그러한 개념은 이해를 하고 있다는 생각이 드는데 생각없이 또 글을 계속 읽다보면 도대체 내가 무엇을 이해하고 있는것인지 모르겠다는 생각을 하게 된다. 그래서 수치적인 예시와 이해하기 힘든 부분들을 읽고 또 읽다가 일단 그냥 넘어가기로 했다. 저자가 서론에서 이미 밝혔듯이 이 책에 나오는 방정식은 장식용에 불과하며 수학의 진정한 핵심인 '개념'에 초점을 맞춰 이해를 하는 것이 더 수학에 가까이 다가가는 것이라 생각했기때문이다. "어째서 수학은 삶의 모든 측면에서 토대를 이루고 있을까? 수학은 어떻게 동전과 유전자, 주사위와 주식, 책과 야구 등 서로 상관없는 영역을 연결하고 있을까? 그 이유는 수학이 생각의 체계이기 때문이다. 그리고 생각은 세상의 모든 문제를 해결할 때 도움이 된다"(8)
수학자처럼 생각하는 법, 을 시작으로 디자인, 확률론, 통계학, 전환점의 다섯부분으로 설명을 하고 있는데 전체적으로 평범하게 살아가고 있는 우리가 실생활에서 쉽게 접할 수 있는 이야기로 세상을 수학적으로 풀이해주고 있다.
첫장에서부터 이 수학책에 대한 흥미를 끌어올리게 해 준 글이 있는데 수학자들은 수학이 언어로 보인다, 라는 것이다. 문학의 은유를 제대로 이해못하는 사람들이 있듯이 방정식의 수학적 언어를 이해못할수도 있다는 것은 찰떡같은 비유처럼 느껴진다.
"인간의 법칙은 유연해서 폐지하거나 재검토할 수 있다. 하지만 기하학의 법칙은 그렇지 않다. 여기에는 자유재량권이라는 것이 없다. 하지만 이는 나쁜일이 아니다. 제약은 창의성을 낳는다. 도형이 무엇을 할 수 없는지 말해주는 법칙은 도형이 할 수 있는 것이 무엇인지 보여주는 사례 연구와 한 꾸러미로 온다. 튼튼한 건물에서 시작해 쓸모있는 종이, 행성을 파괴하는 우주정거장까지 다양한 디자인 프로젝트에서 기하학은 제한을 가하는 동시에 영감을 불어넣어 준다.
따라서 ˝무엇이든 가능해!˝라는 생각은 잊어버리자. 이것은 어린아이들에게 들려주는 동화처럼 아주 달콤하지만 사실은 말이 안되는 이야기다. 현실은 그보다 더 가혹하고, 그래서 더욱 경이롭다"(74-75)
이처럼 디자인의 내용이 딱딱한 기하학, 변화없이 틀에 박혀있는 도형을 다루는 수학이 오히려 그러한 제약을 넘어서기 위한 창의성이 발휘될 수 있다는 것을 보여주고 있다면 확률론이나 통계학은 정직하게 수치가 모든 것을 보여주고 있는 것처럼 보이지만 실제로 그러한 단순 수치가 우리의 일상에서는 심각한 오류를 보일수도 있다는 것을 말해주고 있다.
이 부분에서 특히 저자의 그림들이 빛을 발했다. 기나긴 설명에 집중력이 흐트러질즈음 그림 한 장으로 그 모든 것을 한눈에 이해할 수 있게 정리해주고 있어서 전혀 지루하지 않은 수학책이 되었다.
"통계학은 불완전한 목격자다. 진실을 말하지만, 결코 진실을 전부 말하지는 않는다."(294)
이에 대한 예시는 분배의 문제에는 예민하면서 통계의 문제는 대수롭지 않게 여긴다는 것으로 수학적인 결과의 수치만을 강조하는 것이 세계를 제대로 인식하지 못할 수 있음을 극명하게 보여주고 있다.
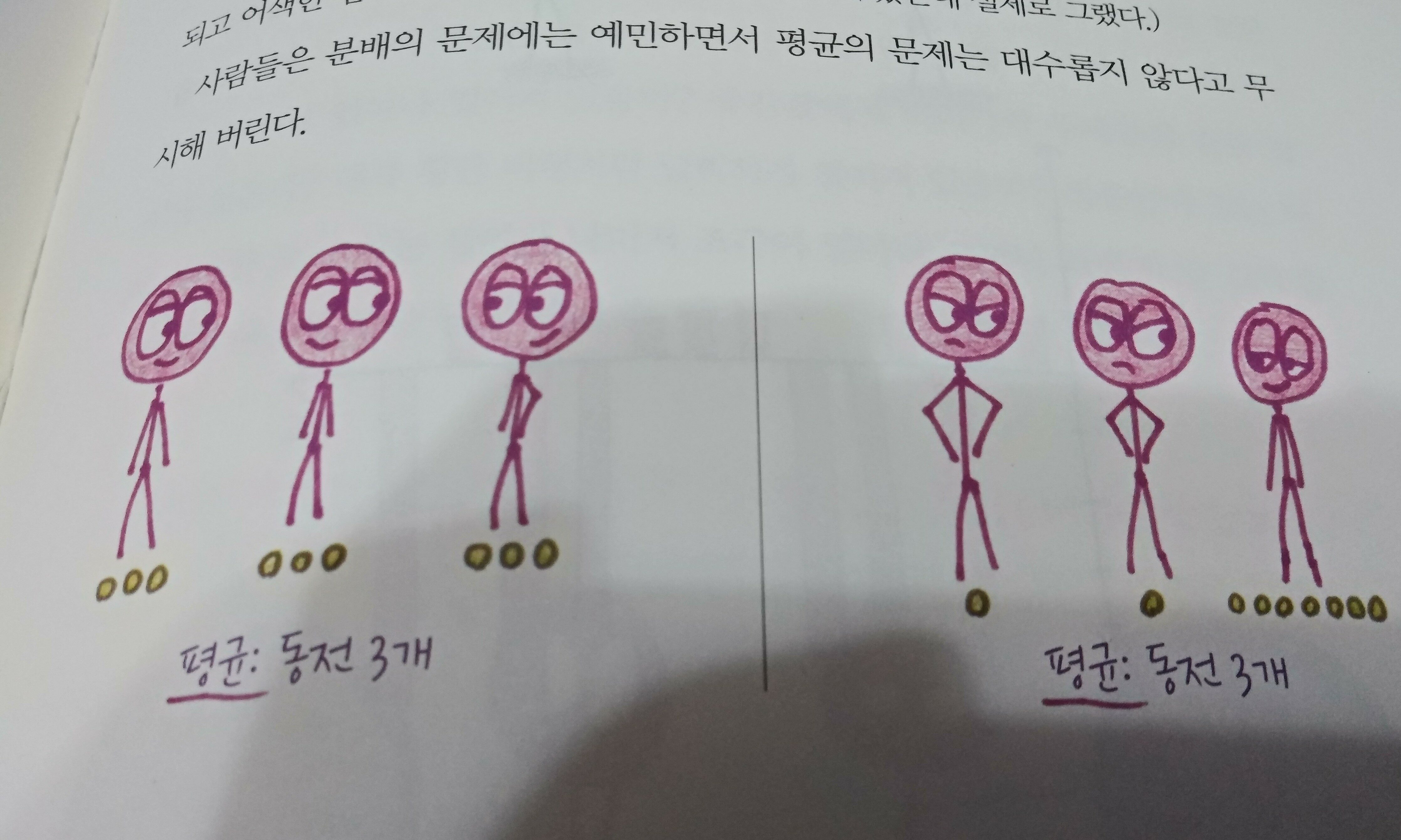
그러고보니 수학자들은 수학을 언어로 읽는 것처럼 나 역시 수학책을 통해 세상의 모든 분야와 연결된 수학의 쓸모를 세계를 인식하는 인문학으로 읽고 있다는 것이 더 명확해지는 것 같다.
그래서 전환점이라는 것 역시 수학에 대한 사고의 변환, 도약으로 받아들여진다. 이상한 수학책,에 대한 이야기를 하며 수학이 숫자만을 말하는 것이 아니라는 것은 인식하게 된 것은 빗방울을 규칙 수열 같은 것으로 수치화하여 파악할 수 있다는 것이 시작이었다고 했는데 이 책의 마무리 역시 그런 느낌이다.
"가끔은 내가 금방이라도 세상을 이해할 것 같은 기분이 들기도 한다. 하지만 뉴스를 보면 세상은 어느새 파악할 수 없는 이상한 모양으로 또다시 바뀌어 있다"(459)
그래서 우리는 끊임없이 수학과 세상에 대한 의문을 갖고 카오스를 코스모스로 전환시키기 위해 노력하고 있는 것일까?