재작년 모스크바 통신에서 '도스토예프스키의 기하학과 부조리극의 기하학'이란 제목으로 올린 글을 옮겨놓는다. 그해 9월 서울에서 몇 권의 책을 소포로 받았었는데, 그것을 계기로 하여 예전에 써둔 걸 정리한 글이기도 하다. 이미지 버전으로 정리해서 창고에 넣어둔다.

오후에 후배가 다른 방 호수로 주소가 잘못 적힌 우편물 수령증을 (다행히도) 갖다 주어서, 구내 우체국에 가서 소포를 찾아왔다. 소식이 감감하던 다른 소포와 함께(알고 보니, 이곳 중앙우체국의 실수인지 배송카드에 수신자 방 번호를 빼먹은 바람에 2주 넘게 우체국 창고에 자고 있었고, 나는 엉뚱하게 ‘보관료’까지 물었다). 후배는 무슨 먹을 게 왔을까 봐 수령증을 건네주며 “오빠, 좋겠어요!”라고 했지만, 두 덩이 소포는 모두 책소포였다(매일같이 책을 사들이는 걸로도 모자라서 책소포까지 받는다!). 하나는 지인에게 논문 관련으로 부탁한 책 3권이고, 다른 하나는 선물로 온 책 2권이다.


선물로 받은 2권은 가라타니 고진의 <언어와 비극>(b출판사)과 수잔 벅 모스의 <발터 벤야민과 아케이드 프로젝트>(문학동네)이다. 책을 받고서 나는 약간 놀랐는데, 그건 책의 부피 때문이었다(아는 사람은 알겠지만, 나는 부피 있는 책들을 좋아한다). 책은 내가 생각했던 것보다 두 배쯤은 더 두툼했다. 우리말로 번역/출간된 고진의 책을 모두 갖고 있는 나로선 이번에 나온 책도 다른 책들과 비슷한 분량의 것이지 않을까 짐작하고 있었는데, 역자의 표현에 의하면 이 ‘가라타니 고진 종합선물세트’는 가볍게 내 예상을 뛰어넘었다!
두 책은 본문 분량이 엇비슷했고 책값도 똑같았는데, (러시아 책값에 좀 익숙해져 있는 나로서는 부담스러울 만한) 상당히 ‘거액’을 들여야 구입할 수 있는 책들이었다. 적어도 액면가로는 내가 모스크바에 와서 가장 비싼 값을 치르고 산 가다머의 <진리와 방법> 러시아어판보다도 더 비싸다(나는 그 책을 헌책방에서 500루블, 즉 20,000원을 주고 샀는데, 이 가격이 현재까지 내가 산 600여권의 책 중에서 최고가이다). 거기에 물론 배송료도 만만치가 않다. 해서, 보내주신 분들의 ‘성의’에 (다시금) 감사를 드릴 수밖에 없는데, 내가 당장에 답할 수 있는 일은 두 권의 책을 애써 읽고 그에 대한 소감을 띄우는 것이리라. 분량상, 그게 가까운 시일 안에 가능할 듯싶지는 않지만, 일단 시작은 하고 본다. 이 글은 그 시작이다.
저녁을 먹고 내가 잠시 읽은 건 <언어와 비극>의 4장 “도스토예프스키의 기하학”이다. 사실 유사한 내용을 이미 <탐구>에서 읽었기 때문에, 특별히 새로운 내용은 아니었다. 그리고, 사실 고진 이전에 나는 도스토예프스키와 (비)유클리드 기하학에 관한 관심을 갖고 있었고(도스토예프스키에 대해 강의할 때면 그 부분을 빼놓지 않았다) 그에 대한 논문을 써볼 생각도 한 적도 있었다. 오래 전에 조사한 바에 의하면, 관련 참고문헌으론 수십 년 전에 <콘티넨트(Kontinent)>란 저널에 도스토예프스키와 (비유클리드) 기하학을 다룬 논문 한편이 실린 바 있다(당시에 그 저널을 구할 길이 없어서 나의 ‘관심’이 흐지부지됐었다). 참고로, 내가 후기 도스토예프스키를 이해하는 키워드는 ‘비유클리드 기하학’과 ‘구원의 변증법’이다.
고진의 논의에서 새로운 건, 그가 마르크스의 <자본론>, 즉 경제학비판을 비유클리드적인 세계, 폴리포니적인 세계에 평행한 것으로 끌어오고 있다는 점이다. 그건 경제학에 대해서 다소 문외한인 나로서는 (고진의 강연을) ‘경청’할 수밖에 없는 대목이기도 하다. 그 강연에 대한 ‘수업료’로 나는 나대로 생각했던/정리했던 비유클리드 기하학을 여기에 옮겨놓는다.

대학원 시절에 나는 '러시아 부조리극과 비유클리드 기하학: 다닐 하름스의 경우'란 리포트를 쓴 적이 있는데, 주로 하름스(D. Kharms)의 부조리극 <엘리자베타 밤>을 자세하고 분석하고 있는 본론을 제외한(*작품이 번역돼 있지 않기 때문에, 라고 적었었는데, 반갑게도 <작가세계>(2006년 겨울호)에 번역/소개되었다) 서론(“부조리극에서의 곡률과 비유클리드 기하학 “)과 결론(“부조리극과 비유클리드 기하학의 교육적 의의”)에서 내용의 일부를 발췌한다(편의상, 각주와 표 등은 생략한다. 참고로 2005년은 하름스 탄생 100주년이 되는 해였다).

이 글-읽기는 러시아 부조리극의 주요 작품들을 비유클리드 기하학적 세계상의 반영으로 보고자 하는 전체 그림의 한 조각이다. 소비에트 NEP(=신경제정책) 시기의 마지막 ‘좌파’문학그룹 오베리우(1927-1930)의 리더, 하름스(1905-1942)의 <엘리자베타 밤>(1927)과 베젠스키(1904-1941)의 <이바노프네 크리스마스>(1938), 그리고 이 ‘마지막 러시아 아방가르드’의 ‘부록’과도 같은 아말릭의 <우리 아줌마는 볼로콜람스크에 산다>(1963)와 망명작가 브로드스키의 <대리석>(1982) 등에 대한 글-읽기가 전체의 나머지 조각들을 이룬다(*이 조각들을 다 맞추는 일 또한 나의 ‘하고 많은’ 프로젝트 가운데 하나이다).


물론 여기에 빠질 수 없는 것은 러시아 부조리극의 ‘원조’ 고골과 그의 <검찰관>(1836)이다. 이때의 <검찰관>은 19세기 풍자 드라마가 아닌 20세기 아방가르드 드라마로서의 <검찰관>이다. 1920년대에 메이어홀드-버전(1926년)과 테렌치예프-버전(1927년)으로 새롭게 공연되었기 때문이다. 특히, 메이어홀드의 공연은 러시아 연극사상 가장 훌륭한 공연으로 평가되고 있으며, 오베리우 작가들에게 많은 영향을 주었다. 이 경우, 고골과 오베리우는 그리 먼 거리에 있지 않다. 그들은 동시대 작가이다. 그렇다면, 그들을 어깨동무하게 해주는 새로운 연극적 세계, 새로운 세계비전은 무엇인가? 우리는 그것을 ‘비유클리드적 세계상’이라 주장하고 싶다.
그러한 우리의 주장을 뒷받침하기 위해서 이 글은 먼저 부조리극에서의 비유클리드적 곡률의 의미가 무엇인지에 대한 문제제기를 간략하게 전개한 후, 비유클리드 기하학의 세계와 그것의 의의를 소개할 것이다(서론). 그런 이후에 하름스의 부조리극 <엘리자베타 밤>에 대한 ‘비유클리드적’ 다시-읽기를 통해 이 작품이 어떤 식으로 새롭게 이해될 수 있는가를 밝히고(본론), 결론에서는 보다 일반론적인 관점에서 부조리극=비유클리드적 연극의 의의를 제시할 것이다.
사실 이러한 작업은 개념적인 차원에서 진행되는 것이 아니라 다분히 은유적인 차원에서 새롭게 시작되는 것이기 때문에, 유클리드적 관점에서 보자면 ‘비뚤어져’ 보일 수도 있다. 하지만 그 비뚤어짐을 통해 우리가 기존에 가지고 있던 고정관념들을 한번쯤 반성해보는 계기가 마련되기를 기대한다. 그럼 어디에서부터 시작해야 할 것인가? 당연히 고골부터인가?
니콜라이 바실리예비치 고골(1809-1852)은 자신이 ‘희극’이라고 명명한 <검찰관>의 이마에 “자기 낯짝이 비뚤어진 건 모르고 거울만 탓한다”는 러시아 속담을 붙여놓고 있는데, 여기서 거울 밖(=현실)의 비뚤어진 낯짝과 비뚤어진 거울상의 대비는 우리에게 유익한 암시를 던져준다. 왜냐하면 부조리극의 이상하고 비상식적인 세계야말로 순진한 관객/독자들이 질타하는 ‘비뚤어진 거울’에 다름아닐 것이기 때문이다. 이 ‘비뚤어짐’의 정도를 비유클리드 기하학에서는 ‘곡률’이라고 부른다.
비뚤어진 거울, 즉 곡률≠0인 거울은 동어반복적으로 현실을 묘사하고 반영(reflect)하는 것이 아니라 그것을 적극적이고 능동적으로 굴절(refract)시킨다. 그러한 굴절 행위를 통해 그것은 일상적인 현실지각, 다시 말해서 유클리드적 지각세계에서는 잘 드러나지 않거나 억지로 지워져 있는 어떤 굴곡들을 복원해낸다. 이때의 굴곡들은 한결같은 굴곡이란 없다는 의미에서 보편적인 것이 아니라 특수한 것이다. 그것은 모든 것을 영속성이 아닌 순수한 시간성과 유연성으로 되돌린다.

바로 그러한 세계가 비뚤어진 거울의 세계, 비유클리드적인 세계이다. 고골은 바로 이 곡률≠0의 세계를 러시아 문학에 도입한 작가이며, 나보코프의 말대로 “공간에서와 마찬가지로 문학적 문체(=스타일)에도 곡률이 존재한다”는 걸 입증한 작가이다. 나보코프는 이렇게 덧붙이고 있다. “푸슈킨의 산문이 3차원적이라면, 고골의 산문은 적어도 4차원적이다. 그는 동시대의 수학자인 로바체프스키에 비유될 수 있다. 로바체프스키는 유클리드를 뒤집어 엎어놓고 이미 한 세기 전에 나중에 아인슈타인이 발전시키게 될 이론들을 발견했다. 만약에 평행선들이 만나지 않는다면, 그것은 그들이 만날 수 없기 때문이 아니라 다른 일을 하기 때문이라는 걸 밝혀놓은 것이다.”
두 가지를 지적하기로 하자. 먼저, 여기서 러시아 문학에서 푸슈킨과 고골의 문체적 전통을 3차원적/4차원(혹은 n차원) 세계의 대비로 본 나보코프의 견해는 비유 이상의 의미를 갖는다. 우리는 고골의 계보를 따르는 도스토예프스키와 몇몇 장식체 산문 작가, 그리고 무엇보다도 부조리극 작가들을 이 4차원적, 비유클리드적 작가의 계보 속에 넣을 수 있을 것이기 때문이다. 이들은 모두 곡률≠0인 세계의 작가들이며, 고골은 그들의 원조이다.
다음, 나보코프는 로바체프스키란 이름을 비유클리드 기하학의 대명사로 사용하고 있는데, 실제로 비유클리드 기하학이 완전하게 마무리되는 것은 독일의 수학자이자 가우스의 제자인 리만에 의해서이다(아인슈타인이 상대성이론에 사용한 것은 리만의 기하학이다). 그래서 비유클리드 기하학은 크게 보아 두 종류로 나뉜다. 우리는 각각을 L-기하학(=로바체프스키 기하학)과 R-기하학(=리만 기하학)으로 구분해서 부르고자 한다. 그럼 이 두 기하학은 표준적인 기하학인 E-기하학(=유클리드 기하학)과는 어떻게 다른 것인가? 먼저 이들의 내용과 차이를 정리해보기로 하자(*비유클리드 기하학에 얼마간 식견이 있는 독자라면 이하 비유클리드 기하학에 대한 자세한 정리는 건너뛰어도 무방하다).


유클리드의 저서 <기하학의 원리>는 서구 문명의 전 역사를 통해 가장 큰 영향을 준 책 중의 하나이다. 이 기하학의 우아함과 아름다움은 2천 년이 넘도록 경탄을 금치 못할 대상이었으며, 수천 개에 이르는 유럽의 정교한 대성당들은 이 기하원리에 따라 축조되었다. 그리하여 유클리드 기하학은 일종의 종교가 되어, 그것과 다른 기하학을 얘기하는 이는 미친 사람이나 이단자로 몰렸다. 그러나 차츰 몇몇 수학자들은 유클리드 기하학의 정리와 씨름해오면서 평면적인 3차원 공간을 대상으로 한 이 기하학의 불완전함에 대해 의문을 품고서 새로운 기하학의 가능성에 도전하기 시작했다. 이에 빌미가 되어준 것은 유클리드의 기하학 공준 중에서 제 5공준이었다.
공리 또는 공준이라는 용어는 자명하고 보편적으로 인정된 진리, 증명없이 수용된 진리를 뜻한다. 하지만 “평면 위에 놓여 있는 두 직선이 제 3의 직선과 만나고 한쪽 방향의 내각의 합이 두 직각보다 작으면, 내각의 합이 두 직각보다 작은 방향으로 충분히 연장하면 그 두 직선은 만난다.”는 유클리드의 제 5공준은 제 1공준: “임의의 두 점 사이에 직선을 그릴 수 있다”나 제 2공준: “임의의 유한한 직선을 무한히 연장할 수 있다” 등과 비교해 볼 때, 서술하기 복잡하고 다소 자명하지 않게 보인다.
평행선 공리라고도 불리는 이 제 5공준을 이와 동치관계인 명제로 다시 서술하게 되면 “직선 L과 L 위에 있지 않은 점 P에 대해서, P를 지나고 L과 평행한 직선은 단 하나 존재한다.”(플레이페어의 공리)라는 것이 되는데, 이 평행선 공리가 다른 공리들과 달리 독립적이라는 사실을 수학자들은 발견하였고, 따라서 그에 모순되는 명제를 채택하는 것과 새로운 공리 체계로부터 결론들을 이끌어내는 것이 적어도 논리적으로 가능하다는 사실을 알게 된다. 그리하여 수학자 사케리(1667-1773) 등은 이 제 5공준을 부정하고 ‘사케리의 사변형’을 내세우는데, 사케리는 A와 B가 직각이고 ‘변AD=변BC’인 사변형 ABCD를 연구하여 유클리드 기하학에서는 AD와 BC는 평행이고 각 D와 C는 모두 직각이지만, 제 5공준을 받아들이지 않을 경우 세 가지 선택이 가능하다고 결론을 내린다.
1. 각 C와 D는 모두 직각이다.
2. 각 C와 D는 모두 둔각이다.
3. 각 C와 D는 모두 예각이다.
여기서 2와 3은 우리의 상식과 직관에 반하기 때문에 얼른 받아들여지지 않았지만, 그럼에도 불구하고 사케리의 가정에 근거하여 정합적인 새로운 기하학이 성립가능하다는 사실이 19세기에 로바체프스키(1793-1856) 등과 리만(1826-1866)에 의해서 발견된다. 이것을 각각 로바체프스키 기하학(또는 쌍곡 기하학)과 리만 기하학(타원 기하학)이라고 부른다(리만의 기하학은 유클리드 기하학의 제 2공준과도 대치된다). 이 두 비유클리드 기하학은 유클리드 기하학의 평행선 공리에 각각 다음과 같이 대응한다.
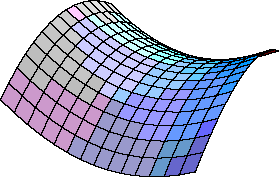
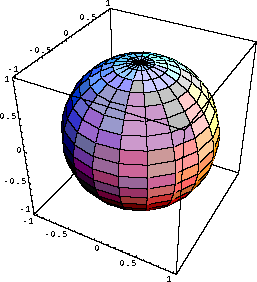
-로바체프스키 기하학: 평명 위에 주어진 직선 L과 L 위에 있지 않은 점 P에 대해서, P를 지나고 L에 평행한 직선이 적어도 두 개 있다.
-리만 기하학: 평명 위에 주어진 직선 L과 L 위에 있지 않은 점 P에 대해서, P를 지나고 L에 평행한 직선은 하나도 없다.
유클리드 기하학이 그리는 세계는 보통 말하는 평면에 비유할 수 있다. 그와 같은 세계, 즉 우리 감각에 가장 친숙한 세계에서 직선은 평면 위에 놓여 있는 직선을 말한다. 비유클리드 기하학이 그리는 세계는, 비록 아인슈타인이 자신의 일반상대성이론에 리만 기하학을 채택했고 시각공간에 대한 한 연구는 로바체프스키의 비유클리드 기하학에 의해 가장 잘 묘사될 수 있다는 결론에 도달했다고 하지만, 다소 상상적인 세계이다.
현재 수학자들이 인식하고 있는 사실은, 세 종류의 기하학과 관련된 세 종류의 세계가 높은 곳에서 바라보면 서로 다르게 보이지만 아주 근접한 거리에서 바라보면 서로 잘 구분할 수 없다는 것이다. 이러한 관찰은 모델의 표면을 이용하여 쉽게 그려볼 수 있다. 먼 거리에서 넓은 시야로 바라보면, 가짜 구(트럼펫 2개를 연결한 모양)와 진짜 구 그리고 평면들이 서로 혼동되는 일이 없다. 그렇지만 이들에게 가까이 다가서서 좁은 시야로 바라보면 이들은 모두 똑같은 평면으로 보인다. 이 사실은 우리의 선조들이 곡면으로 된 지구 표면을 평평한 것으로 잘못 판단하였던 추론과정과 일치하였을 것이라고 생각한다면 그리 놀랄 일은 아니다.
유클리드는 현대인이 인식하고 있는 지구에 적합한 기하학을 건설한 것이 아니라, 분명히 지구는 평평하다는 가정에 따라 건설하였다. 일상적인 용도(거리의 실측 등)에서는 유클리드 기하학과 비유클리드 기하학과의 차이는 거의 보잘것없는 정도라 하겠으나 문제의 소재는 거기에 있는 것이 아니다. 그 각각이 합리적이고 인간경험에 적합하다는 데 있다. 비유클리드 기하학에 관한 가장 중요한 사실은 그것이 유클리드 기하학과 마찬가지 정도로 정확하게 물리적 공간의 성질을 기술하는 데 사용될 수 있다는 것이다. 즉 유클리드 기하학은 물리적 공간의 필연적인 기하학은 아닌 것이다. 즉 그것은 경험적인 것이지 결코 선험적인 것이 아니다.


이러한 결론은 전통적 세계관뿐만 아니라 근대적 세계관에 대해서도 중대한 도전의 의미를 갖는다. 뉴튼 물리학에 대응하여, 이 세계가 인간의 오성에 의해 구성된 것임을 밝힘으로써 철학적 사유에 있어서 코페르니쿠스적인 전환을 가져오고 근대의 철학적 세계관을 정립한 칸트(1724-1804)는 <순수이성비판>(1781)에서 이렇게 주장한 바 있다: “공간은 기하학의 종합적 판단을 선험적, 즉 보편적 필연적인 것으로 만든다. 만일 공간 그 자체가 경험적인 것이라고 한다면 기하학도 선험성을 상실하게 되고 학문으로서의 가치를 잃는다. 이것은 우리의 기하학에 관한 상식에 어긋난다. 따라서 기하학이 선험적이기 때문에 이 학문의 기초를 이루고 있는 공간 역시 선험적이어야 한다.”
이때 칸트가 말하는 기하학은 유클리드 기하학이며, 그는 유클리드 기하학의 원리가 선험적이기 때문에 우리가 지각하는 공간 또한 선험적인 것이라는 결론을 내린다: “유클리드 공간의 개념을 결코 경험적인 근원에 의한 것이 아니라 피할 수 없는 사고의 필연성이다.” 즉 그에 의하면, 공간은 인간의 마음에 직관적으로 이미 존재하는 체제이고 유클리드 기하학의공리와 공준은 인간의 마음에 부과된 선험적인 판단이며, 이 공리와 공준 없이는 공간에 대한 어떠한 무모순의 추론도 불가능하다는 것이다. 따라서 평행공준의 독립성을 주장하며 새로운 기하학을 제시하는 것은 칸트의 철학에 정면으로 도전하는 셈이었고, 결과적으로 유럽의 사상계를 지배하던 권위적인 견해와 맞서야 하는 엄청난 부담을 안게 되었다.
하지만 우리는 선험적 공간에 대한 칸트의 확신이 잘못된 것이라는 것을 안다. 적어도 논리적으로는 전혀 다른 기하학이 가능하며, 따라서 유클리드 기하학은 선험적인 것이 아니라 경험적인 것이다. 이럴 경우, 자연의 법칙은 인간의 창조의 산물이다. 신이 아닌 우리가 우주의 법칙을 부여하는 자이다. 자연의 법칙은 인간의 서술이지 신의 규정이 아닌 것이다. 여기서 비유클리드 기하학의 이교적 성격, 다신론적/무신론적 성격을 짚어볼 수 있다(*혹은 폴리포니적 성격).
공간의 유클리드적/비유클리드적인 이중적 본성에 대한 철학적 통찰은 수학이 유클리드 기하학에서 비유클리드 기하학으로의 단계를 거친 이후에야 가능했다. 그때까지 물리학은 기하학의 공리를 물리학의 자연에 대한 기술에 있어서 자명한 기반으로 간주해 왔다. 그러나 만일에 여러 가지 종류의 기하학이 수학적으로 대등한 것으로서 간주된다면 이 기하학 중 어느 것이 물리적 실재에 적용될 수 있는가라는 문제가 생겨난다. 반드시 유클리드 기하학을 사용할 필요성은 없는 것이다.
수학은 물리학이 관찰과 실험에 의해 여러 개의 기하학 중의 하나를 선택할 수 있도록 다양한 가능적 형태를 제시한다. 그래서 비유클리드 기하학의 발견 이후 물리적 공간과 가능적인 공간의 이중성이 인식되었다. 이때 수학은 가능한 공간을 시사하고, 물리학은 그 중에서 물리적 공간에 대응하는 것을 결정하게 된 것이다. 그리하여 이제 수학은 인간 정신의 임의의 창조로서 출현하게 되었으며, 수학은 우리가 살고 있는 세계가 우리에게 필연적으로 지시된 어떤 근본적인 것으로 나타나지 않게 되었다.


이 사건을 E. T. 벨은 이렇게 서술하고 있다. “간단히 말하면, 소설가가 저자이자 창조주로서 등장 인물의 성격과 대화 및 상황을 창조하는 것과 똑같은 방법으로, 수학자는 자신의 뜻대로 자신의 수학적 체계가 근거할 공준을 고안해낸다. 소설가와 수학자 모두는 소재를 선택하고 취급하는데 환경에 의해 조건지워질 수 있다. 그러나 그들은 초자연적이고 불멸의 필연성에 의해 어떤 성격을 창조하거나 어떤 체계를 발견하도록 강요받지는 않는다.”(<수학을 만든 사람들>)
그리고 바로 이런 점에서 비유클리드 기하학이 이룬 가장 중요한 성취는 새로운 지적인 흐름을 형성시킨 점이라고 말해진다. 그래서 그것이 가져온 지적인 비약은 그보다 3세기 앞서 일어난 코페르니쿠스 혁명에 비견할 만하다. 코페르니쿠스가 지구를 우주의 중심이라는 거만한 지위에서 끌어내린 것처럼, 로바체프스키와 리만은 유클리드 공간을 기하학에서의 절대적 위치에서 끌어내렸다. 공간의 곡률이란 개념을 발명한 리만의 업적은 수학자들에게, 어떤 기하학도, 어떤 공간도 인간의 지각작용의 필연적인 양식이라고 생각되어서는 안된다는 사실을 가르치고 있다. 그것은 절대적 공간에 마지막 숨통을 끊음으로써, 19세기 물리학에서 ‘절대자’의 종말을 고하는 최초의 종소리가 되었다(*여기까지가 서론이다. 언급한 대로 본론을 건너뛰고 결론으로 넘어가기로 한다).

러시아 부조리극의 원조는 고골이며, 로바체프스키와 동시대인이었던 고골의 문학세계에서부터 비유클리드 기하학적 세계상의 반영을 읽어낼 수 있다는 주장은 앞에서 우리가 이미 던진 것이다. 그런데 비유클리드 기하학에도 L-기하학과 R-기하학의 서로 다른 종류가 구분되듯이, 고골의 계보를 따르는 비유클리드적 작가들의 문학세계도 크게 두 가지로 구분될 수 있을 듯하다. 그것은 3차원적 현실세계를 어떤 값으로 굴절시키느냐는 문제인데, 가령 곡률이 양수(곡률>0)인가 음수(곡률<0)인가에 따라서 변환되는 비유클리드적 세계상은 분명 서로 차이가 날 것이다.
나보코프는 고골의 경우를 두 종류의 비유클리드 기하학을 구분하지 않은 채로 이해했지만, 사실 고골은 비록 두 종류의 양상이 다 드러내 보여주는 듯도 하다. 즉 수축적인 세계와 팽창적인 세계가 그에게서는 어느 정도 공존하고 있는 것이다. ‘납작해진 사람들’(subman)의 테마는 분명 L-기하학(곡률<0)의 세계이지만, 곳곳에서 보이는 등장인물들의 장광설과 과대망상은 R-기하학(곡률>0)의 세계처럼 보인다. 몇몇 예외적인 경우는 있지만, 그의 세계는 상상력과 먹을 것이 남아도는 풍족한 세계이다. 예컨대, <검찰관>에서 흘레스타코프의 과장된 자기자랑과 허풍을 보자.
안나 안드레예브나: 정말로 운치가 있는 호화로운 무도회가 열리겠죠?
흘레스타코프: 그야 말씀하실 것도 없습니다. 테이블 위엔 수박이, 이를테면 7백 루블짜리 수박이 놓여 있습니다. 수프는 냄비에 담은 채로 파리에서 곧장 배로 가져옵니다. 뚜껑을 열면 김이 확 오르는데 그건 이 세상에서 비길 것이 못 되는 겁니다.(...)

<외투>의 주인공 아카키 아카키예비치가 받던 연봉이 4백 루블 정도였던 것을 감안하면 7백 루블짜리 수박은 대단한 허풍이 아닐 수 없다. 고골의 언어는 이 수박만큼이나 과장되어 있으며 문체적으로 풍족하다. 그래서 수박의 구 모양처럼 양의 곡률을 가진 세계이다. 즉 그의 세계에서 삼각형의 내각의 합은 분명 180°보다 크다. 그런 관점에서 보자면, 도스토예프스키의 문학세계는 고골의 비유클리드적 세계를 극한까지 밀어부친 경우라는 점에서 문체적 적자(適者)라고 할 수 있다.
실제로 도스토예프스키는 로바체프스키 기하학을 알고 있었으며(*<카라마조프의 형제들>에서 보다 ‘노골적으로’ 비유클리드 기하학을 참조한다), <지하생활자의 수기>(1864)에서 2×2=4(합리주의)의 논리라는 것을 유클리드 기하학의 논리로 본다면 그가 주장하는 2×2=5의 인간적 의지/욕구의 세계는 그러한 의지와 욕구에 의해서 굴절된 비유클리드적 세계의 논리라고 할 수 있을 것이다. 그것을 단순하게 합리주의/비합리주의로만 이해하는 것은 미흡한데, 비유클리드적 세계에도 자체의 논리가 있기 때문이다(욕망에도 법칙이 있다!).


또한 그의 후기 대작들에서 보여지는 것이지만, 그의 작품들에서 시간은 현실시간과는 관계없이 늘어나고 팽창하여 일상적인 시간에서라면 도저히 다 담길 수 없는 사건들까지도 담아낸다. 거기에 인물들의 과장된 감정과 장광설은 문학사에서 달리 유례가 없을 정도이다. 그런 의미에서 우리는 고골-도스토예프스키의 계보를 R-기하학의 세계상과 연관지어 생각해볼 수 있을 것이다. 반면에 하름스의 <엘리자베타 밤>에서도 알 수 있지만, 부조리극의 세계는 축소되고 납작해진 수축된 세계이다. 인물들의 말도 일상적인 경우보다 늘어나는 것이 아니라 줄어든다.
이반 이바노비치 (의자에 뛰어오르며): 펜실베니아의 목동이여 영워어-어-하-아!
엘리자베타 밤 (의자에 뛰어오르며): 이반 이바-아-아-아!
아빠 (상자를 보여주며): 상자는 나므-으-으-으-로.
이반 이바노비치 (의자에서 내려오며): 아-아-안-녀-어.
아빠: 와아서 바-아-아.
엄마: 루-우-우-우-우!
언어뿐만 아니라 작품의 파토스에서 우리는 두 세계를 구별할 수 있다. 고골과 도스토예프스키의 세계가 파토스(pathos)의 거울상인 바토스(bathos)의 세계를 보여준다면, 부조리극의 세계는 (새로 이름을 붙이자면) ‘하토스(xathos)’의 세계쯤이 될 것이다. 하토스의 세계는 웃음(유머)과 공포(경악)가 공존하는 세계이다. 그것은 고골이 <검찰관>의 마지막 1분 30초 동안의 정지 장면에서 관객들에게 기대한 충격적 효과를 원조로 가지고 있다.

<검찰관>의 무대지시에서 특별히 이 장면에 대해서 언급하고 있는 주의사항: “배우들은 특히 마지막 장면에 주의를 돌려야 한다. 마지막 대사는 모든 사람들에게 순간적으로 쇼크 같은 것을 주어야 한다. 일동은 한 순간에 자세를 바꿔야 한다. 경악의 외마디 소리는 마치 가슴에서 터져 나오듯이 모든 부인들의 입에서 동시에 터져 나와야 한다. 이 같은 주의 사항이 준수되지 않으면 모든 효과는 없어질 수 있다.” 이런 효과가 유발하는 정서적 파토스는 잘 정의할 수 없는 x의 세계이고, 기괴한 웃음(xa xa xa)의 세계이다.
이미 우리는 서두에서 비유클리드 기하학이 가져온 코페르니쿠스적 전환에 대해 언급한 바 있다. 그것은 한 가지 이성, 즉 도구적/계산적 이성에만 맹목적으로 의지해온 근대적 합리성에 대한 적극적인 도전과 비판의 뜻을 갖는다는 것이었다. 모든 굴곡을 지우고 평면화하며, 사고의 편익을 위해 곡선을 직선으로 대체하고, 세계를 엄격한 주-객관의 구별에 기초한 인식론의 대상으로 전락시킴으로써 가져온 폐해를 우리는 여러 역사의 현장들에서 확인할 수 있다. 하이데거의 의하면, 이러한 근대의 근본과정은 세계를 상(Bild)으로 정복하는 것이다.

“상이라는 말은 이제 표상하면서 산출하는 행위의 총체적 상을 뜻한다. 이 총체적 상 속에서 인간은 모든 존재자에게 척도를 제공하고 원칙을 이끌어가는 그러한 존재자일 수 있는 입장을 마련하기 위해 투쟁한다. 이 입장은 세계관으로 자신을 확실히 하고 분류하고 언표한다.(...) 인간은 모든 사물을 계산하고, 계획하고, 사육하기 위해 무제한의 폭력을 행사한다. 연구로서의 학문은 이런 세계 안에서 스스로를 자리매김하는 데 있어 불가결한 한 형태, 즉 근대가 그 참여자에게 알려지지 않은 속도로 자신의 본질 성취를 몰아치는 행로들 중의 한 형태이다. 이러한 세계관들에 대한 투쟁과 함께 근대는 자신의 역사에 있어서 결정적이고 가장 지속력 있는 국면에 접어든다.”(<세계상의 시대>)
여기서 모든 사물을 표상으로 만들면서 “모든 사물을 계산하고, 계획하고, 사육하기 위해 무제한 폭력을 행사”하는 근대적 주체를 우리의 맥락에서 유클리드적 주체로 바꿔 부를 수 있을 것이다. 물론 이러한 근대적 주체가 산출한 결과는 그것의 폐해에 대해 눈감아주게 할 만큼 눈부신 것이기도 했다. 하지만, 우리는 잠시의 미망에서 깨어나 이 ‘당신들의 천국’의 세계에서 더 이상 지탱되어서는 안되는 것들의 목록을 작성하고 적극적으로 항의해야 한다. 그럼 구체적으로 무엇에 대해서인가?
가령 “m×n수의 무고한 다른 생명들을 구하기 위해, n명의 무고한 사람들에게 고문이 가해져도(죽임을 당해도) 옳은 일인가? 만일 그렇다면, n과 m의 적정한 수치는 얼마인가?” 이런 유의 물음에 대해 잘 근거지어진 이론적인 대답이 존재한다고, 즉 이런 유의 도덕적 딜레마를 푸는 알고리즘이 존재한다고 생각하는 사람들에 대해서이다. R. 로티의 말을 빌면, 그들은 여전히 신학자나 형이상학자이다. 그런 사람은 인간이 존재하는 요점을 결정하며 동시에 책임의 우선 순위를 수립해주는, 시간과 기회를 넘어선 어떤 질서를 믿고 있다. 다시 말하지만, 그들로부터 파시즘과 스탈린이즘 사이의 거리는 결코 먼 거리가 아니다.
도대체 무슨 알고리즘이 존재할 수 있을까? 가령 유클리드 기하학에서라면 반지름이 r인 원의 둘레 C를 구하는 공식은 C=2πr로 간단하게 표시될 수 있지만, L-기하학에서는 아주 복잡한 수식으로 표시되고 R-기하학에서는 아예 공식을 간단하게 표현할 수 없다. 우리가 대하는 삶의 굴곡들이 낳고 있는 문제들은 이렇듯 아주 복잡한 문제들이고 정답을 가질 수 없는 문제들이다. 2×2=4라는 단순한 알고리즘 하나만 가지고 모든 문제를 해결할 수 있다는 무지와 오만이 얼마나 많은 불행을 가져왔으며 얼마나 많은 작가들을 제물로 희생시켜 왔는가!
우리에게 필요한 것은 시간과 기회를 넘어선 그러한 어떤 질서가 없다고 믿는 아이러니스트 지식인들이고 작가들이다. 우리식으로 말하자면 그들은 비유클리드적 지식인들이고 작가들이다. 그리고 부조리 작가들은 바로 그러한 아이러니스트 작가, 비유클리드적 작가의 대표적인 한 유형으로서 그 의의가 평가될 수 있을 것이다. 넌센스의 세계를 말하면서 그들은 센스의 세계, 상식적인 세계가 더 이상 우리가 가질 수 있는 유일한 세계가 아니라는 걸 가르치고 폭로한다. 세계제작의 유일한 방법(the way)이 있는 것은 아니라 다양한 방법들(ways)이 있다는 걸 그들은 문학적 실천을 통해 예시한다. 그들은 삶에 대한 새로운 개념, 사물에 대한 새로운 접근방법을 제시한다. 그런 의미에서 그들은 훈육자이며 교육자이다. ‘다닐 하름스의 경우’를 통해 그러한 점이 제대로 지적되었기를 희망한다.

하름스는 “시간과 공간, 존재에 관하여”란 자신의 한 에세이에서 흥미로운 주장을 펼치고 있다. 세계의 존재의 문제를 놓고 그는 이런 식으로 논리를 전개한다.
1. 존재하지 않는 세계는 존재한다고 말해질 수 없다. 왜냐하면 존재하지 않기 때문이다.
2. 통합적이고 동질적이며 연속적인 어떤 것으로 이루어진 세계는 존재한다고 말해질 수 없다. 왜냐하면 그런 세계에는 어떠한 부분도 존재할 수 없으며 부분이 없다면 전체도 없는 것이기 때문이다.
3. 존재하는 세계는 이질적이어야만 하고 부분을 가져야만 한다.(...)
여기서 그가 강조하는 것은 세계가 정말로 존재한다는 자기-주장을 전개하기 위해서는 이질적, 이종적이어야 하고 또 그에 따른 당연한 결과이지만 반드시 부분들을 가져야만 한다는 것이다. 이것은 이미 우리가 앞에서 말한 바대로 “직선 L과 L 위에 있지 않은 점 P에 대해서, P를 지나고 L과 평행한 직선은 단 하나 존재한다.”는 한 가지 사실만을 고집하는 유클리드 기하학적 세계관, 단의성의 신화에 대한 비판과 맥락을 같이 한다.
그는 자신의 문학적 상상력의 세계에서 그와는 대비되는 진정으로 존재하는 세계를 그려내고자 했다. 부분(조각)들로 이루어진 세계, 그리고 다양한 언어와 장르와 문체들의 병치를 통해 이어적이며 다성적인 말들의 잡화상을 차려놓은 것이다(스탈린-기계에 대항하는 우리의 언어-기계들!) 이들 말들의 충돌과 불일치, 부조화 속에 진정으로 생생하게 살아있는 현실, 리얼한 현실이 담길 수 있다고 그는 믿었으리라. 하지만 그는 그러한 현실, 그러한 사회의 작가가 아니었다. 그런 의미에서 ‘죽은 혼들’의 세계라는 고골의 예언적인 진단은 아직도 유효하다.

진정 살아 있는 삶의 세계가 우리 현실에 보다 밀착되지 못하고 극장의 무대라는 공간에만 한정되어 버린 것은 비단 아방가르드 작가들, 혹은 하름스만의 불행은 아니었으리라. 그것은 진정으로 다양하고 새로운 삶을 꿈꾸었던 모든 ‘좌파’ 지식인-작가들의 불행이며 비극이 아니면 안 될 것이기 때문이다. 우리의 시를 창문에 던지면 창이 깨진다는 걸 믿는 사람은 아직도 얼마나 적은 것일까! (구부러짐과 굽신거림을 혼동하는 사람들은 또 얼마나 많은 것일까!)
강물은 오늘도 무서운 속도로 상류의 물들을 하류로 실어나르고
둔덕의 풀꽃들은 그림자 길게 휘어 달빛을 잡는다
그리고 나는 세상은 휘휘 젓는 직선에 괴로워한다
등이 구부러진 과일들, 등이 구부러진 노인들, 등이
구부러진 황소, 야! 아예 온몸이 구부러짐의 시작의 끝인 시작의
둥근 공과도 같은 하루는 있는 것일까
-박용하, <구부러지는 것들>
04. 9. 9./ 06. 08. 23.