* 나의 애인과 친해지는 법
부제 ; 수학 공부 잘하기
- 다음 문제를 풀어봅시다.
문1) 11+27=?
문2) 배 11개와 배 27개를 합치면 모두 몇 개인가?
두 문제 중 어느 문제가 쉽습니까?
(모두 다 쉽다... 그러면 이야기 진행이 안 되죠. 상상의 나래를 펴서 초등학교 시절로 돌아간 기분으로)
- 1번과 같은 문제를 계산문제(calculation problem)이라 하고 2번과 같은 문제를 서술형 문제(story problem)이라고 합니다.
- 수학문제를 푸는 단계는 4단계가 있는데
첫째, 문제를 이해한다.
둘째, 풀려는 목표와 자료의 관계를 찾고 그것을 눈에 보이게 표시한다.(관계식을 구한다.)
셋째, 관계식을 풀이한다.(계산한다.)
넷째, 문제와 답을 음미한다.
- 문1)은 문2)에서 문1)로 진행하는 첫째 단계를 이미 생략한 문제입니다. 그러나 문1)같은 문제에 두려움을 느끼는 사람도 많은데, 그것은 수학기호를 정확히 이해하지 못했기 때문입니다.
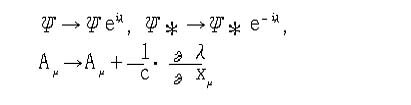
위 공식은 게이지 변환(gauge transformation)에서 나오는 공식입니다. (게이지 변환 : 전기를 띤 하전입자와 전자기장 사이의 상호작용을 다루는 이론에서 사용되는 변환) 삼지창 같은 그리스 문자와 몇 개의 알파벳, 그리고 화살표 등이 있다는 것 외에 무엇을 뜻하지 모릅니다. (저도 모릅니다. 묻지 마십시오.) 단지 장황한 말로 설명할 것을 매우 간결하게 알아보기 쉽게 표현했다는 것은 압니다.
- 초등학교 때 산수문제 중 아이들에게 공포를 주던 문제가 있었는데 그것이 바로 응용문제
문3) 50% 농도의 50ml의 식염수와 25% 농도의 100ml 식염수를 혼합하면 몇 %의 식염수가 되는가?
이 문제는 농도 식염수 등의 용어를 사용하여 간단한 계산문제에 혼돈을 주고 있는 서술형 문제입니다.
* 수학 시험에서의 수학 재능이란
위 네 단계를 모두 잘해야 수학 시험을 잘 보는데, 첫째 단계와 둘째 단계를 선천적으로 잘하는 사람이 있습니다. 이런 사람을 수학에 재능이 있다고 이야기합니다. 즉 문1)을 읽고 문2)과 같다고 생각하며, 문2)를 읽고 문1)로 쉽게 전환되는 것을 이릅니다. 하지만 이 과정도 학교 수업을 통해 배우게 됩니다. 세 번째와 네 번째는 훈련이 필요합니다. 물론 네 단계를 모두 쉽게 하는 사람도 있습니다.
- 저의 이야기를 하면 첫 번째와 두 번째는 수학의 본질로 생각하는데, 세 번째와 네 번째는 비본질적인 것으로 생각하여 정신의 집중이 느슨해지면서 실수를 많이 합니다. 예를 들면 ‘다음 방정식의 정수의 해의 곱은?’이라는 문제에서 해를 1, 2, 1/2로 구해 놓고 정수해라는 함정에 주의하지 않아 정답은 2인데, 저는 1로 답을 표시합니다. 틀린 것을 보고 별로 속상해하지도 않았습니다. 왜냐하면 수학 본질의 문제를 해결했으므로. (그래서 점수는 그저 그랬습니다.)
- 애인(수학)과 친해지는 법은 우선 두려움을 버리십시오. 그리고 네 단계 중에서 어느 것에 취약한가를 생각한 후 그것에 집중하십시오. 문1)과 문2) 모두 쉽지 않습니까? (문3)과 함께 풀어보세요.)