수직垂直에 대해서...

요즘 박홍규전집을 읽고 있는 중이다..

박홍규전집 중 『형이상학강의1』을 읽고있는데  그 중 맨 앞부분에 나오는 글인 "고별강연'장에서 흥미로운 구절이 있었다. 인용해 보자.



 

 

 

 

 

 

 

 

 

	" 기하학을 가지고 얘기를 해봅시다. 예를 들어 각 변이 두 자인 이런 정사각형의 면적을 구하라는 문제가 있다고 합시다. 물론 우리는 쉽게 4평방자라고 답하겠죠. 그런데 우리에게 경험적으로 주어진 것, 다시 말하면 실제 우리에게 데이터로 주어진 것은 연장성 속에 들어 있고, 물리적 세계physical world속에 들어 있습니다. 이 정사각형은 흑판 위에 하얀 색깔로 그려진 것이죠. 그래서 이것을 실지로 잽니다. 재어서 이것의 면적은, 이 단위 면적이 네 개 있는 것이라고 말합니다. (...)그러나 또 하나의 문제가 생겨요. 왜 정사각형의 면적을 내는 데 변을 곱한다는 법칙이 성립하느냐 하는 문제에요. 직각 사각형의 변을 곱하면 그 면적이 나온다는 것은 언제든지 되풀이 되니까 하나의 법칙으로 성립하는데. 그 근거가 어디에 있냐는 것입니다.(...) 그러니까 문제는 그것이 직각 사각형이라는 데에 있습니다. 물론 플라톤은 이런 말을 하지 않지만, 만약 플라톤적인 입장에서 그것을 설명하자면 수직이라는 데에 그 요체가 있다는 것입니다. 수직이란 공간에 있어서 반대되는opposite 것을 찾았을 때, 공간으 반대되는 부분으로 나누었을 때 성립하는 것입니다. 그것은 즉, 수직하는 두 직선은 공통점이 하나도 없다, 그러니까 그것을 곱하면은 그들이 둘러싸고 cover있는 면적은 하나도 빠지지 않고 나온다는 이론입니다.(...)요컨대 플라톤의 입장에서는 변을 곱하면 면적이 나올 수 있다는 법칙은 수직각이라는 그 도형의 형태 때문이라는 것입니다. 도형의 형태가 그것을 요구한다는 겁니다. 그 도형의 형태를 우리는 형상(eidos)이라 합니다. "

(박홍규, 박홍규전집2. 형이상학강의1, 민음사, 18-19 쪽. 강조는 인용자)

이 구절에서 박홍규씨가 강조하는 것은 수직垂直, perpendicularity이다. 가로선과 세로선이 만나서 각도가 수직이 되었을 때 "반대opposite"라는 질質적 차이를 가지게 되는데 이처럼 반대되는 특성이 만나서 하나의 새로운 형태 혹은 "형상"(eidos)를 이루게 된다는 요지의 설명이다. 그는 특히 플라톤에게서의 형상은 아리스토텔레스와는 달리 각각의 형상은 서로 다른 고유한 성질을 가지고 있기 때문에 구체적 맥락안에서 각각의 형상이 어떠한 모습을 가지는지 살펴보아야 한다는 점을 강조한다.

특히 기하학에서의 수직 혹은 직각은 플라톤의 이와 같은 형상eidos 개념에서 중요한 설명도구인 것으로 보인다. 그래서 직각에 대해서 한번 생각해 보았다. 직각과 관련된 논의를 시작하기 위해 먼저 기하학에서의 원주각에 대해서 살펴보자. 원주각에 대한 설명을 인용해 보면,

" 원둘레각이라고도 한다. 원주 위의 한 점 P에서 그은 두 개의 현 PA, PB가 이루는 각 ∠APB를 P가 속하지 않는 호 AB에 대한 원주각이라고 한다. 또, 원주 위에 호 AB가 있을 때 그 호와 원의 중심 O가 만드는 각 ∠AOB를 그 호 AB 또는 현 AB에 대한 중심각이라고 한다([그림 1]).

하나의 호에 대한 원주각의 크기는 그 호에 대한 중심각의 크기의 1/2과 같다. ([그림 1])에서 ∠APB=1/2 ·∠AOB이다. 그러므로 호 AB에 대한 원주각 ∠APB는 원주 위의 점 P의 위치에 관계없이 항상 일정하다([그림 2]). 또, 켤레호에 대한 원주각은 보각(補角)을 이룬다. ([그림 3])에서 ∠APB+∠AEB=180°이다. 지름 AB의 원주각은 직각을 이루며([그림 4]), 이것은 그리스의 수학자 탈레스(BC 640년?∼BC 546년?)에 의하여 발견되었다. (출처: 네이버 백과사전)"

 

 우리가 중학교에서 배웠던 것처럼 한 호에 대한 원주각의 길이는 [그림 2]에서 보이는 것과 같이 항상 일정하다. 이 말은 어떤 원에서 호의 길이가 한번 주어지면 그것의 원주각은 호가 원의 어디에 위치하던지, 원주각이 어느 곳에 위치하던지 항상 일정하다는 이야기이다. 그 중에서도 특히 흥미로운 원주각은 [그림 4]다. [그림 4]에서는 바로 앞에서 박홍규씨가 언급한 "직각"이 등장한다. 이 때 재미있는 사실은 원주각이 직각일 때 이에 대응하는 호의 길이는 반원이 되며 현은 원의 반지름이 된다는 사실이다. 결국 직각이라는 원주각은 원전체의 둘레 길이의 반에 해당하는 호의 길이와 원 전체를 가로지르는 지름의 길이를 나타내는 요소로 동시에 작용한다는 것을 보여주는 셈이다.

그런데 앞에서 박홍규씨는 "직각"은 두 개의 성질이 서로 반대opposite된다는 것을 보여주는 역할을 하며 직사각형의 면적을 구하는 경우를 예를 들면서 설명한 바 있다. 그렇다면 원주각에서는 어떤 두 개의 반대되는(opposite) 성질들이 서로 결합하고 있을까?

바로 직선과 원이다. 직각인 원주각은 [그림 4]에서 보는 것처럼 원과 직선이라는 서로 반대되는 기하학적 성질을 서로 결합하고 있다. 직각은 직선인 지름과 반원과 같은 서로 반대되는 기하학적 질들을 원주각이라는 형태로 서로 연결시키는 역할을 하고 있는 것이다.

직각이 가지는 특징은 사실 이것만이 아니다. 박홍규/플라톤도 언급하고 있지만 직각은 "공간의 반대되는 부분"을 서로 결합함으로써 1차원인 두 직선을 2차원의 평면으로 변화시킨다. 이런 특징때문에 직사각형의 넓이는 가로 곱하기 세로를 하면 유도되는 것이다. 더 나아가 직각은 가로와 세로의 결합으로 만들어지는 2차원 공간 뿐만 아니라 3차원 공간에서도 결정적으로 작용한다. 다음 좌표를 살펴 보자.

 

위 좌표계는 x, y, z 라는 세 좌표로 이루어져 있다. 이처럼 x, y, z 세 좌표로 표시되는 공간을 우리는 3차원 공간이라고 한다. 그런데 여기서 주목해야 할 부분은 이 세 좌표들 각각이 바로 직각을 이루고 있다는 점이다. 2차원인 평면이 x와 y 두 좌표가 수직일 때 만들어지는 것이라면 3차원 공간은 x, y, z라는 세 좌표가 직각을 이루자 탄생하는 공간인 것이다. 

직각은 이처럼 서로 상반된 두 가지 요소를 결합하는 측면이 있다. 그럼으로써 탄생하는 것은 새로운 질이요 새로운 차원의 공간인 것이다. 직각의 이러한 수학적 특징을 가장 잘 드러나는 것이 또 있는데 바로 삼각함수이다.



알다시피 삼각함수는 위 그림과 같은 원 내부에 θ  가 주어지면 그 각과 원 위의 한 점 P좌표(x,y)가 이루는 직각삼각형이 만들어 내는 함수이다. 이 삼각함수를 이용해 우리는 sin 곡선과  cos 곡선 그리고 tan 곡선을 그릴 수 있다. 이 때에도 직각은 중요하게 작용한다. 다음 그림을 보자.

        

 

[그림 1]처럼 sin곡선은 일정한 주기를 가지는 주기함수이다. 그것의 주기는 라디안으로 표시하면 2π 즉 360°이다. 그런데 π 는 알다시피 60분법으로 180°이고 그것은 직각 즉 π/2 (90°)의 정수배로 표현될 수 있다. 삼각함수의 각변환도 결국 직각(π/2)의 정수배에 의해서 이루어 진다. 주어진 각이 nπ/2 + θ  이면, 다시말해 90° × n ± θ  (단 n은 정수)이면 sin곡선은 cos곡선과 tan곡선으로 변환될 수 있다. cos 곡선자체가 sin곡선을 x축 위에서 음의 방향으로 π/2 만큼 움직여서 생기는 곡선인 것도 위의 [그림 2]에서 확인 할 수 있다. 때문에 cos(x)을 다음처럼 표현하기도 한다.

 

 이처럼 sin곡선과 cos곡선 tan 곡선이 서로 변환하는데 직각은 결정적인 요소로 작용한다. 그런데 삼각함수는 비단 기하학과 같은 수학에서만 발견되는 것이 아니다. 자연계에서도 이러한 삼각함수에 의해서 나타나는 곡선과 형태를 자주 발견할 수 있다. 빛의 움직임을 연구할 때에도 소리의 움직임을 연구할 때도 sin곡선이나 cos곡선과 같은 삼각함수를 이용해야 한다. 그것들은 파동이라는 형태로 시공간상에서 운동을 하기 때문이다.  수학에서의 특정한 형태가 자연계 내부에서도 반복적으로 나타난다는 것은 자명한 사실이다. 또 그렇기 때문에 우리는 수학을 자연과학의 도구로 중요하게 사용하는 것이다.

지금까지 살펴본 것처럼 직각은 수학에서 그리고 물리학에서 중요한 역할을 담당한다. 그런데 이와같은 "직각"을 박홍규/플라톤은  "공간에 있어서 반대되는opposite 것"이 만났을 때 성립하는 것라고 이야기하고 있다. 서로 반대되는 질質이 만나서 하나의 형상(eidos)를 만들게 되는데 그것은 아리스토텔레스가 말하는 일반적인 의미에서의 형상이 아니라 하나의 질을 가진 유일하며 고유한 형상이라는 것이다. (박홍규, 형이상학강의1, 21-22쪽) 이와 관련해서 박홍규씨는 소위 "데이터"의 중요성을 강조한다. 데이터라는 것은 사물을 "재는" 행위에서 획득 할 수 있는데 직각도 결국 이러한 재는 행위에 의해서 나온 결과물인 것은 주지의 사실이다. 박홍규씨의 책 『형이상학강의 1』에서는 이러한 "데이터" 그리고 형상과 관련된 플라톤과 아리스토텔레스의 중요한 논의가 언급되고 있다. 이와 관련해서는 다른 기회에 정리해 보도록 하겠다.  

사학비리..이것 좀 너무하는 것 아닌가?

평소에 그들은 늘 3불정책의 폐지를 주장하면서 학생들의 선발권을 좀더 보장해줄 것을 요구해왔던 터다. 그런데 이번 김포외고 시험문제 유출사건이 일파만파로 번지는 모습..그리고 연세대 총장부인의 편입학 비리사건등등을 보면서 그들이 과연 그런 소리를 할 자격이 있는지 의문이다.

만약 지금처럼 각종 비리와 뒷돈이 오가는 사학들의 행태를 묵인한채로 3불정책이 폐지되고 이명박씨의 공약처럼 외고가 수백개로 늘고한다면 그 결과는 눈에 불을 보듯 뻔한 것이 아닌가? 사학의 비리를 근절하지 못하고, 그들에게 무한한 학생선발의 자율을 보장한다면 이는 마치 고양이에게 생선을 맡기는 것과 뭐가 다른 것인지.

한국처럼 입시에 목매달고 사는 사회에서 입시부정이나 비리의 발생이라는 것은 상당히 심각한 문제라 아니할 수 없다. 그나마 돈없고 빽없는 사람들이 공정한 경쟁의 룰을 배경으로 자신의 노력과 실력만으로 좋은 배경을 가질 수 있는 유일한 방법이 바로 대학입학에서의 경쟁이라고 한다면 이제는 이 마저도 돈의 힘에 의해서 좌우되고 만다는 것을 보여주는 꼴 아닌가? 3불정책의 폐지로 외고가 비약적으로 늘고, 대학은 기여입학제를 실시하고, 대학생 선발은 그들 자율에 맡기고, 또 뒷구멍으로 비리를 마음대로 저지르게 내버려 둔다면 이제 이 사회는 볼장 다 본 사회인 것이다.  

관련된 기사 하나를 퍼와 본다.

[ 한겨레] 성형외과 등 인기과 독차지

연세대 치의학과 교수나 동문의 자녀들이 상당수 치의학과에 편입학한 것(〈한겨레〉 10월31일치 9면)처럼 연세대 의대 교수의 자녀들도 상당수 편입학을 통해 의대에 들어간 것으로 나타났다.

〈한겨레〉가 1999~2006년 연세대 의대 편입학 합격자들의 신상을 확인한 결과, 부모가 의대 교수인 이들은 모두 6명인 것으로 집계됐다. 98~99년 복수전공으로 의대에 들어간 의대 교수 자녀도 3명이다. 연대는 지난해까지 해마다 의대 정원의 10%인 10명 가량씩 편입생을 뽑았는데, 의대 교수 자녀들이 2000~2002년 3년을 제외하고 해마나 한두 명씩 편입학했다.

특히 한 사립대 생물과학과를 나온 편입생 ㄱ씨는 아버지가 의대 부학장으로 재직할 때 의대에 편입했다. 한 의대생은 “부학장이면 의대에선 ‘넘버3’로 막강한 영향력을 갖고 있는 자리”라며 “부학장 자녀가 편입시험을 본다는 것을 채점 교수들이 모르진 않았을 것”이라고 말했다. 이에 대해 해당 교수는 “편입학 문제는 대학 입학관리처에서만 입장을 표명하기로 했다”며 취재에 응하지 않았다.

지난해에는 세브란스병원장의 아들도 연세대 생물학과를 졸업한 뒤 의대에 편입학했다. 병원장은 “의대 교수 자녀 중에도 편입에 떨어지는 경우가 많다”며 “내 아이는 학부에서 모두 에이(A) 학점을 받아, 편입학 과정에 내 힘이 작용했다는 말은 어불성설”이라고 말했다.

이름 밝히길 꺼린 한 의대 교수는 “편입학 때 서류와 시험으로 3배수를 뽑는데 이 과정에는 개입하기 어렵다”며 “면접 때 교수 자녀들에게 ‘인지상정’이 개입되는 것은 부정할 수 없을 것”이라고 말했다.

하지만 이재용 연세대 입학처장은 “입학원서에 부모 등 가족 사항을 기재하지 않고, 적법한 심사과정을 거치기 때문에 교수 자녀가 특혜를 받아 입학할 수 없다”고 말했다.

의대생들은 부모나 친인척이 의대 교수인 편입생 및 재학생들을 ‘로열 패밀리’라고 하고, 이들의 상당수가 본과 졸업 뒤 전공을 선택할 때 피부과, 성형외과 등 인기과로 가는 것을 ‘로열 코스’라고 한다.

한 의대 졸업생은 “대학 입시를 통해 의대에 들어올 실력이 안 되는 교수 자녀의 경우, 아예 편입을 염두에 두고 생물, 화학 등 기초과학 전공을 택하게 한다는 얘기도 돌고 있다”고 말했다. 실제 의대 교수 자녀인 편입생 6명 모두 학부에서 기초과학을 전공했다.

칸트의 수학론에 대한 오독: 브라우어와 진은영의 경우

앞의 글에서 브라우어(L.E.J. Brouwer)가 "직관주의(intuitionism)"으로 자신의 수학기초론을 명명한 배경에는 칸트철학에 대한 오독에서 비롯된 것이라는 이야기를 한 바 있다. 이번 글에서는 이에 대해서 보다 자세히 다루어보려고 한다.

브라우어는 수학의 기초에 대한 스스로의 입장을 세우면서 칸트 철학에서 그 유사함을 본 것으로 보인다. 칸트는 그의 저서인 『순수이성비판』에서 수학을 "직관intuition"이라는 개념을 사용해 정의하면서 그것이 "선험적 종합판단"임을 논하였다. 이러한 칸트철학을 참조하여 브라우어는  스스로를 직관주의라고 부르게 되었다는 것이다. (박세희, 수학의 세계, 서울대학교출판부,312쪽. 참조) 이는 브라우어가 칸트철학을 자신이 생각한 것처럼 수학을 인식주관으로부터 독립적인 실재로 가정하지 않고 인식주관에 의해서 구성적으로 이루어진다고 보는 종래의 견해에  기초한 결과이다. 그런데 사실 이는 칸트철학에 대한 오독이다.    

칸트는 『순수이성비판』에서 수학은 "선험적 종합판단"이라고 규정한 적이 있다. .(칸트, 순수이성비판 1, 아카넷, 225쪽 참조) 그러면서 그것이 순수논리에 의한 개념적 구성물이 아니라 왜 "직관을 보조로"한 학문인지 설명한다. 칸트의 설명을 다소 길지만 인용해 보자.

"처음에 사람들은 '7+5 =12'라는 명제는 '칠'과 '오'의 합이라는 개념으로부터 모순율에 따라 귀결되는 분석적인 명제라고 생각함직하기는 하다. 그러나 좀더 자세히 고찰해 보면 '7'과 '5'의 합이라는 개념은 두 수를 하나의 수로 통일한다는 것 이외에는 아무것도 포함하고 있지 않으며, 이로부터 그 두 수를 포괄하는 이 하나의 수가 무엇인가는 전혀 생각하지 않음을 알게 될 것이다. '십이'라는 개념은 내가 순전히 칠과 오의 저 통일을 생각하는 것으로써만 이미 생각되는 것이 결코 아니다. 나는 그러한 가능한 합이라는 나의 개념을 한동안 분해할 수는 있지만, 그렇다 해서 거기서 '십이'와 마주치지는 못한다. 그러므로 두 수 중 하나에 대응하는 직관을 보조로 취해 예컨대 다섯 손가락이나 또는 (세그너가 그의 산술학에서 했던 것처럼) 다섯 개의 점을 그렇게 해서 하나씩 직관에 주어지는 다섯의 단위들을 일곱의 개념에 덧붙임으로써 사람들은 이 개념들을 넘어갈 수밖에 없다.왜냐하면 나는 먼저 수 7을 취하고, 5라는 개념 대신에 직관으로서 내 손의 손가락들을 보조로 취함으로써, 나는 수 5를 형성하기 위해 앞으로 함께 취했던 단위들을 이제 저 나의 그림에서 하나씩 수 7에 더하고, 그렇게 해서 수 12가 생겨나는 것을 보게 되니 말이다. 5에 7이 더해져야(이 부분의 강조는 칸트가 직접 했다. 그는 5에 7을 더한다는 것이 분석적으로 유도되는 것이 아니고 직관적으로 주어진다는 사실을 강조하기 위한 의도로 보인다.)한다는 것을 나는 7 + 5의 합의 개념에서 생각하기는 했지만, 이 합이 수 12와 같다는 것은 거기에서 생각하지 않았다. 그러므로 산술의 명제는 항상 종합적이다. " (강조는 필자)

 (칸트, 순수이성비판 1, 아카넷, 225-226쪽)

 

브라우어는 칸트의 이러한 설명으로부터 즉 "산술의 명제는 항상 종합적이다"라는 것의 설명으로부터 자신의 구성주의적 수학을 직관주의로 호명한 것으로 보인다. 그런데 여기서 주의해야 할 부분은 칸트가 비록 산술의 명제를 '분석적'인 것이 아니라고 말하고 자연수의 합과 같은 산술이 "직관을 보조"로 한 것이라고 말했다고 해서 그러므로 칸트의 수학에 대한 입장을 객관적인 수학적 개념(concept)나 대상으로부터 독립적인 실재를 가정하지 않은 순수하게 구성적(constructive)이며 주관적인 학문이라고 규정했다고 볼수는 없다는 점이다.

 칸트철학의 본체를 보여주는 『순수이성비판』은 수학이나 물리학과 같은 개별학문들 처럼 "선험적 종합판단"을 자체 내에서 수행하기 위한 작업이라기보다는 이 "선험적 종합판단이 어떻게 가능한가"라는 물음 즉, 그것의 토대란 무엇인가라는 물음에 대한 대답이다. 때문에 그의 철학은 기존 형이상학과 개별 학문들의 토대에 대한 전면적 재검토가 될 수 있었다.  이러한 물음에 답하기 위해 칸트는 "초월적 감성학"으로 『순수이성비판』을 시작한다. 다름아닌 바로 "직관"의 개념규정으로부터 책을 시작하는 것이다.

"어떤 방식으로 그리고 어떤 수단에 의해 언제나 인식이 대상들과 관계를 맺든지 간에 그로써 인식이 직접적으로 대상들과 관계를 맺는 것은 그리고 모든 사고가 수단으로 목표하는 것은 직관이다."

(칸트, 순수이성비판 1, 아카넷, 239쪽)

그리고 "직관은 오로지 우리에게 대상이 주어졌을 때에만 생기며" 대상은 "감성을 매개로 우리에게 주어"지고 이 "감성만이 우리에게 직관들을 제공한다. 그러나 그것들은 지성에 의해 사고되며 지성으로부터 개념들이 생겨난다." (같은 책, 239쪽)

그런데 칸트는 시간과 공간과 같은 표상들은 "순수한 직관"이면서 동시에 그것은 "경험적인 것이 아니라 선험적(a priori)"이라고 말한다. 여기에서 선험적인 것은 경험에 선행한다는 의미이므로 인식의 "주관"안에서 찾아져야 한다. 특히 시공간과 같은 직관은 "신에게서나 가능함 직한 "근원적 직관"이 아니라 일종의 "파생적 직관"이라는 점에서 말이다.(칸트, 순수이성비판 1, 아카넷, 36-37쪽 참조) 그러나 이 때 주의해야 할 것은 비록 이 "파생적 직관"이 주관적인 것이기는 하지만 그것은 “객관의 현존에 의존적이고, 그러니까 주관의 표상력이 그것에 의해 촉발됨으로써만 가능한” 직관이라고 칸트는 말한다. 다시말해 시간과 공간과 같은 직관은 단순히 주관적인 파생적 직관이 아니라 객관적 실재성을 내포한 “근원적-파생적 직관”이라는 것이다. 

그리고 시간, 공간(에 대한 직관)은 대상의 현존이 없이도 가능한 “상상력”이다. 그것은 “주관을 벋어나면 그 자체로는 아무것도 아닌” 순수 감성적 직관이기 때문이다. (같은 책 225쪽) 그리고 동시에 그것은 무질서하고 잡다한 현상에 질서를 부여하는 작용을 한다. 칸트는 그것을 “감각기능(감관)에 의한 선험적인 잡다의 일람(一覽)작용”, “상상력에 의한 이 잡다의 종합” 또는 “근원적 통각에 의한 이 종합의 통일”(같은 책 317)과 같은 말로 시공간에 대한 직관을 표현한다. 그런데 이 시공간에 대한 순수직관은 지성처럼 순수한 형태로 분석적 사고의 양식을 만들어 내는 능동성에 기반한다기보다 대상의 감관에 주어질 때에 비로소 그것에 질서를 부여하는 방식으로 작용한다는 점에서 수동적인 것이다.

시공간에의 직관은 이처럼 대상적 인식이 가능했을 때에만 주어지는 수동적 성격을 가지면서 그와 동시에 무질서하고 잡다한 현상에 질서를 부여하는 능동성을 가진다. 그러면서 그것은 자기 자신이라고 할수 있는 “상상력”에도 기초로서 작용한다. “양”이나 “다수성” “전체성”과 같은 범주들의 적용에도 마찬가지이다. 다양한 대상들을 단일한 하나의 시간 혹은 공간으로 표상할 수 있다는 점에서 특히 그렇다. 소위 “대상일반”의 인식도 그래서 가능해 진다. 


그런데 대상들을 통일시키고 그것의 지각을 가능하게 하는 시공간(에의 직관)은 대상들의 현존을 가능하게 하는 실재적 본질이다. 다음 설명을 들어보자. 

 “다시말해 공간, 시간은 그 자체로는 주관적이고 그런 의미에서 ”관념적“인 것이지만, 현상하는 객관들과 관련해서는 실재적, 곧 객관적으로-실재적이다. 공간,시간은 그 자체만으로 볼 때나 경험적 직관 너머에 있는 어떤 대상, 가령 초험적인 사물과 관련해서 볼 때는 순전히 아무것도 아니지만 그럼에도 경험적인 직관, 곧 경험적으로 직관함과 경험적으로 직관되는 것을 동시에 가능하게 한다.”(백종현, 같은 책, 42쪽. 강조는 필자) 


이러한 특성을 칸트는 “경험적 실재성” 혹은 “초월적 관념성”이라고 규정한다. 현상들과 관련해 그것에 객관적 실재성을 부여하는 면에서는 “경험적 실재성”을 가지지만 동시에 인간의 주관을 벗어나서는 “그 자체로는 아무것도 아니”고 현존하는 대상 없이도 인간의 인식 내에 “상상력”으로 작용할 수 있는 주관이라는 측면에서는 “초월적 관념성”을 가진다는 이야기이다. 완전히 객관적 대상에 귀속되는 실재도 아니고 그렇다고 순수한 인식주관으로만 환원할 수도 없는 수동성을 가진다는 이러한 양면성. 그것이 시간, 공간에 대한 직관이다. 

칸트가 앞서서 7+5 =12 라는 수학적 결과는 두 수의 합이라는 “개념”에 의해서 유도되는 것이 아니라 그것을 하나하나 세어보는 행위를 통해어 깨닫는 “직관”의 보조에 힘입은 바 유도되는 “선험적 종합판단”이라고 한 것도 바로 이런 맥락에서 이해해야 한다. 

그런데 이와는 달리 정수론에 심취하여 칸토어의 혁명적 업적을 부인했던 크로네커, 그리고 수학적 귀납법의 유용함을 근거로 환원공리를 비판한 푸앵카레(모리스 클라인, 수학의 확실성, 사이언스북스 참조) 그리고 자연수 내에 존재하는 “직관적”성격을 내세워 자신의 입장을 직관주의라고 명명한 브라우어 등은 모두 칸트의 수학에 대한 입장을 단순히 구성적이고 주관적인 것으로만 간주했고 이는 칸트 철학에 대한 오독임이 분명하다. 다시말해 그들은 위에서 이야기한 직관의 초월적 성격, 객관적 실재로서의 측면은 제대로 직시하지 못하고 그것의 한 측면 즉, 주관으로서의 성격만 보았던 것이다. 그런데 칸트의 수학론을 이처럼 잘못 이해한 사람들은 비단 직관주의자들 뿐만이 아니다. 러셀과 프레게와 같은 논리주의자들도 마찬가지이다. 그들은 칸트가 수학을 “선험적 종합판단”으로 규정한 것을 두고 잘못이라고 말하면서 수학의 수학의 경험적이고 직관적인 측면을 무시하고 “분석적”이고 “논리적”인 면만을 강조하려고 하였던 것이다.

 가라타니 고진은 칸트가 이처럼 수학을 “선험적 종합판단”이라고 규정한 것을 두고 철학 내에 “타자”를 도입한 “철학 역사상 처음 있는 일”로 평가한다. (가라타니 고진, 트랜스크리틱, 한길사, 87쪽) 다시 말하면 칸트가 수학을 “선험적 종합판단”으로 규정한 것은 바로 철학에 대한 자기반성이요 비판이라는 것이다. 고진을 인용해 보자.

“내 생각에 형식적인 공리계에 의해 수학을 기초짓는다는 몽상은 수학 고유의 것이 아니다. 그 몽상은 분석판단을 유일하게 확실한 것으로 간주하는 형이상학에 의해 초래된 것이다. 칸트가 부정하려고 한 것은 그러한 사고이다. 그러나 그것은 그러한 형이상학이 스스로 밀어붙인 수학에 의거하는 이상, 수학에서 행해져야 한다. 반대로 수학에서 행해진 것은 수학을 모범으로 삼아온 철학으로 되던져질 것이다. 괴델의 ‘초수학’적 비판은 그러한 의미를 지닌다. 따라서 그것은 칸트의 초월론적 비판과 연결되어 있다. 지금 돌이켜 볼 때 칸트가 수학을 ‘종합판단’이라고 간주한 것은 옳았다고 해야 한다.”
(가라타니 고진, 트랜스크리틱, 한길사, 116쪽)

이처럼 고진은 칸트철학이 수학에 대해서 가지는 입장을 인식주관에 의해서만도 아니요, 혹은 객관적 실재로서만도 아닌 이율배반적인 초월성을 가진 것으로 비교적 정확하게 인식한 것이다. 아카넷판 『순수이성비판』의 역자인 백종현씨도 고진의 입장과 크게 달라보이지 않는다. 그런데 이와는 달리 칸트에 대한 오독은 국내학자들에게서도 마찬가지로 나타난다. 『순수이성비판, 이성을 법정에 세우다』라는 책을 쓴 진은영씨가 대표적인 경우이다. 

“그가 선천적 종합판단의 대표적 모델로 삼고 있는 것은 7+5 =12와 같은 수학적 판단이다. 칸트에 따르면 7+5=12는 우리가 사과나 돌멩이를 가지고 경험적으로 세어보았기 때문에 타당한 것이 아니다. 일일이 세어보지 않아도 우리는 이 판단이 맞다는 것을 알 수 있다. 만일 그것을 세어보아야만 알 수 있다면 우리는 수학을 할 수 없을 것이다. 우리는 손가락, 발가락으로 세면서 수학적 판단을 배우게 된다고 흔히 생각하지만 수학적 판단의 보편성과 필연성은 경험과 무관하다. 누군가 1234+1001=2235가 맞는지 묻는데 예전에 세어보았던 경험을 돌이켜야 한다든가 세어본 경험이 없어서 1234개의 사과와 1001개의 오렌지를 창고에 넣으며 수를 센 후에만 대답할 수 있다면 수학적 판단은 현실적으로 불가능하고 불필요하다. 우리는 손가락이나 돌멩이로 세는 일 없이도 수학적 판단의 보편성과 필연성을 확신한다. 도대체 이와 같은 보편성과 필연성이 어디에서 유래하느냐라는 물음에 대해 칸트는 우리의 주관적 형식에서 온다고 대답하는 것이다.”
(진은영, 순수이성비판 이성을 법정에 세우다, 그린비, 66쪽. 강조는 필자)

이 구절의 앞에서 그는 분석판단과 종합판단의 차이점을 설명하면서 위에서처럼 칸트가 설명한 산술명제의 예를 들고 있다. 하지만 위와같은 진은영의 설명은 선험적 종합판단의 예라기보다는 오히려 분석판단에 대한 설명으로 보아야 한다. 그는 7+5=12라는 수학적 결과는 “경험적인 것이 전혀 섞이지 않은 순수한 판단”이라고 그는 말하고 있기 때문이다. 

그런데 우리가 앞서서 문제의 칸트의 구절을 직접 인용해 본 것처럼 칸트는 분명 7+5=12라는 결과는 단순히 개념적 수들의 합에 의한 결과가 아니라 “7을 취하고 5라는 개념 대신에 직관으로서 내 손의 손가락을 보조로 취함으로써, 나는 수 5를 형성하기 위해 앞으로 함께 취했던 단위들을 이제 저 나의 그림에서 하나씩 수 7에 더하고, 그렇게 해서 수 12가 생겨나는 것을 보게 되니 말이다.(....)7+5의 합의 개념에서 생각하기는 했지만 이 합이 수 12와 같다는 것은 거기에서 생각하지 않았다. 그러므로 산술의 명제는 항상 종합적이다.”라고 분명히 말하고 있지 않은가? 

진은영은 칸트가 7+5=12의 예를 들면서 수학은 “선험적 종합판단”이다라고 설명한 것을 분명 오독하였고 때문에 무엇인가 어색함을 느낀 것 같다. 그래서 추가적으로 물리적 판단을 이야기하면서 그것의 "선험적 종합판단"의 경험과의 연관성을 이야기한다. 더불어 칸트가 수학과 물리학의 경우를 “나누어 설명하려고 한 이유는 분명하지 않다”고 말하면서 마치 선험적 종합판단이 경험적이지 않은 것과 경험적인 것 두 개로 구분된다는 방식으로 이야기한다. 그런데 여기에서 우리가 주의해야 할 것은 수학과 같은 “선험적 종합판단”도 마찬가지로 경험적 직관을 포함한다는 것이고 또 직관자체가 비록 경험을 포함함에도 불구하고 그것의 가능근거로서 직관이 작용한다는 점에서 “선험적a priori”이라는 표현을 칸트는 사용하고 있다는 점을 주의해야 한다. 경험은 달리말하면 선험적이기 때문에 직관적인 것이고 직관적이기 때문에 선험적인 동시에 경험적인 것이므로. 이러한 양면성 혹은 이율배반을 이해하는 것이 칸트 철학에서 주요한 핵심이다.

괴델에 대한 오해

10월, 당신의 추천 영화는?

지금까지 괴델을 브라우어와 같은 직관주의자로 알고 있었다.

그런데

위의 책을 보고 그것이 그에 대한 오해라는 것을 알았다.

사실 그는 플라톤과 같은  "관념론적 실재론"자라는 것이다. 후기의 후설처럼..

플라톤적인 이데아를 수학에서 처음부터 끝까지 관철한 학자라는 것.

이제는 잘 알지도 못하는 수리철학책도 들춰봐야 하는건가?

러셀의 <수학의 원리>같은 수리철학책은 왠만하면 가까이 하지 않으려고 했는데..ㅜ.ㅜ 

봐도 얼마나 이해할수 있을런지는 미지수지만 말이다.

이쯤에서 수리철학계의 계보를 정리해 보자.

먼저 논리주의

논리주의는 러셀에 의해서 칸토어의 집합론 속에 역리가 있다는 것을 발견하고 그를 통해서 수학을 전통적 철학에서의 논리학의 한 분과로 인식하려는 관점이다. 이에 따라 수학의 기초를 기호논리의 형식으로 재구성하려는 것을 목표로 한다.

원래 논리주의는 19세기의 심리주의와 형식주의에 대한비판으로 고틀롭 프레게가 <개념서술>,<산술의 기초>등과 같은 저서를 통해서 발전시킨 분야이다. 객관적이고 보편타당한 학문의 기초로서 수학의 기초를 확립하기 위해 그는 경험이나 직관에 의존하지 않는 순수논리의 용어만으로 수들을 정의하려 하였다. "산술명제가 순수 논리법칙만으로 증명가능한 논리체계"라는 것을 제시하려고 시도한 것이다. 그런데 이러한 프레게의 작업은 처음에는 잘 알려지지 않았다. 그런데 러셀에 의해서 그의  공리체계에 모순이 있음이 알려지게 됨으로써 비로소 되늦게 조명받게 된다. 그 모순이 바로 오늘날 우리가 이른바 "러셀의 역설"로 알고 있는 것이다.

러셀의 역설에 대해서 잠시 살펴 보자.

다음 2종류의 집합이 있다고 가정해 보자.

1종집합: 자기 자신을 원소로 포함하는 집합

2종집합: 자기 자신을 원소로 포함하지 않는 집합

이 때 "2종집합 전체"로된 집합을 R이라 할때, R은 1종인가? 2종인가?

 가정1: 만일 R이 1종이면 R은 스스로가 원소인 집합이다. 그런데 R은 2종인 집합이다. 따라서 R을 1종이라고 가정하면 2종집합이라는 전제에 모순이 발생한다.

가정2: R이 2종이면 R은 스스로 원소는 아니다. 그런데 앞에서 R은 "2종집합 전체"라고 했기 때문에 R은 전체 집합 R의 원소가 되어야 한다. 따라서 이것도 모순.

결론: R은 1종도 2종도 아니다.

집합론에서 발견된 이러한 러셀의 역설은 당시 수학계에 큰 파장을 미치게 되는데  그것을 어떻게 다루는지에 따라 후에 논리주의와 형식주의 그리고  직관주의로 나뉘게 되는 계기가 된다.

한편, 힐베르트에 의해서 최초로 체계화된 형식주의는 러셀의 논리주의와는 달리 논리법칙을 절대화하지 않는다. 대신 수학적 공리계를 “형식화”한다. 다시 말해 수학적 공리나 정리를 수학적 기호만으로 표현하려고 한 것이다. 이러한 형식적 체계를 “힐베르트의 프로그램”이라고 부르는데 이 체계 안에서는 형식적 체계에 의해 표현된 수학적 대상은 일단 무의미한 것으로 간주된다. 반면 이러한 형식적 체계와는 달리 그 체계의 ‘증명’은 하나의 ‘기호열’이 됨으로써 그자체 수학적 대상으로 전화하고 그것에는 의미가 있는 것으로 취급된다. 이 때의 수학을 일명 “초수학” 혹은 “메타수학”이라고 부른다. 그것의 주요한 목표가 바로 형식적 체계의 “무모순성의 증명”이었던 것이다. 


이를 다시 정리하면 다음과 같다. 형식화되지 않은 비형식적 수학이 있고 그 다음에 이를 체계화/형식화한 형식적 수학, 그리고 다시 그것을 증명하는 초수학 이렇게 3단계의 수학이 존재한다는 것. 형식적 수학은 비형식적 수학을 체계화함으로써 얻어지고 또 이 형식적 수학의 기초는 초수학이라는 메타적 방법으로 그 무모순성이 증명되는 구조를 이루게 된다. 


다만 이때 주의해야 할 것은 이와같은 체계의 증명라는 것은 무한번의 과정을 반복함에 의해 주어지는 것이 아니라 유한한 횟수의 조작을 통해서 가능해야 한다는 것이다. 형식적 체계의 조작과정을 무한번 반복하게 되면 결국에 가서는 영원히 그 체계의 정당성은 증명될수없는 모순에 빠지기 때문이다. 이러한 입장을 소위 “유한의 입장”이라고 하는데 이는 직관주의의 형식주의비판에 대한 대응으로 형식주의진영 내에서 마련된 것으로 보인다. 


그런데 흔히 수학의 토대를 무너뜨린 것으로 평가되는 괴델의 불완전성 정리도 사실은 이러한 힐베르트의 형식주의를 철저하게 실행시킨 결과 탄생한 것이다. ‘산술의 무모순성’을 증명하기 위한 수학의 형식화가 거꾸로 자신의 불완전성을 ‘증명’하게 되는 역설적 상황을 맞게 된 것. 이처럼 형식주의는 어떻게 보면 자체 내에 모순을 가지고 태어난 유토피아적 기획이긴 하였으나 괴델의 불완전성 정리를 통해 스스로의 한계를 보여줄 수 있었다는 점에서 거꾸로 이 공리계의 형식화라는 야심찬 목표는 어떻게 보면 자신의 이루려는 목표를 충분히 달성한 셈은 아닐까? 더불어 형식주의는 이러한 공리계의 형식적 조작을 통해 아직도 유의미한 수학의 발전을 이룰 수 있다는 것을 보여주고 있다. 흔히 공리적 집합론으로 불리우는 ZF집합론이 그 한 예이다. 

이러한 형식주의에 대한 비판의 대표적인 케이스가 바로 브라우어(L.E.J. Brouwer)에 의해 직관주의라고 명명된 입장이다. 직관주의는 수학적 대상이 실체적으로 인간의 정신과 독립적으로 존재하는 것이 아니라 인간의 정신 혹은 의식에 의해 구성되어지는  지식으로 간주한다. 이는 상대적으로 수학적 대상의 실체성과 진리의 가능성을 전제로하는 힐베르트의 형식주의에 대한 당대의 가장 강력한 비판이었다.

 

직관주의가 형식주의를 비판할 때 사용하는 논거중에서 가장 대표적인 것이 바로 배중률이다. 배중률(the law of excluded middle; LEM)이란 가령 명제 A가 성립한다면 그것은 A이거나 아니면 A가 아니거나 둘 중 하나는 반드시 성립해야 한다는 원리이다. (논리기호로 표현하면 A v ~A)이는 아리스토텔레스 이래로 동일률과 모순율과 더불어 고전적 형식논리학의 3대 원리 중 하나이다. 수학에서는 이 배중률이 유한집합 내에서만 사용된다면 모순이 발생하지 않는다. 그런데 문제는 이것을 무한에 적용시켰을 때 발생한다.

가령 원주율인 π를 예를 들어서 생각해 보자. 알다시피 π는 소수점 이하자리의 수가 반복되지 않는 무한대의 십진수로 주어지는 무리수, 더욱 정확히는 초월수이다. 동경대에서는 이 π를 컴퓨터를 이용하여 32억 2천만 자리까지 구한 적이 있다고 한다. 이 독특한 성질, 즉 소수점이하자리의 수가 무한대로 반복되지 않고 계속 이어진다는 성질로부터 우리는 배중률을 두고 발생한 형식주의와 직관주의간의 입장차를 분명히 확인해 볼 수 있다.

 π는 흔히 3.14로 소수점 둘째자리까지만 사용한다. 그런데 사실 그 소수점이하의 수는...

3.14159265358979323846264338327.........................

이런식으로 무한히 계속될 수 있다. 그런데 소수점 이하 762자리에서 767자리에 처음으로 9가 연속적으로 6번 등장한다. 「.........134999999837........」이렇게 말이다. (요시나가 요시마사. 괴델 :불완전성 정리. 전파과학사 ,126쪽 참조) 그런데 문제는 이처럼 9가 연속적으로 나올수 있는 가능성은  소수점이하 자리의 수가 무한일 때 그 가능성이 완전히 열려있다는 점이다. 가령 9가 연속적으로 100번이 나올수도 1000번이 나올 수도 있는 것이다. 그런데 지금까지 알려진 바에 의하면 예컨대 동경대 컴퓨터로 계산한 소수점 32억 2천만 자리에는 그런 9의 연속이 아직까지는 발견되지 못했다는 것이 문제다. 또 그리고 그것이 몇번째 자리에서 출현할지 아무도 모른다는 것. 

바로 이 때 배중률이 적용될 수 없다는  문제점이 노출된다. 이 경우 배중률에 의하면 소수점 아래 몇번째 자리수에서 9가 100번 연속될지 알수없기  때문에 우리는 그것을 A이거나 혹은 A가 아니거나 하는 식으로 확정할 수 없다는 한계에 놓이게 되는 것이다.  

이와 관련된 일화를 하나 소개하면, 브라우어가 힐베르트의 괴팅겐수학클럽에서 원주율과 관련된 난점을 이야기 했을 때 한 청강자가 다음과 같이 반문했다고 한다.

"당신은 원주율 π를 10진법으로 표현했을 때 9가 10회 연속해서 나타나는지 아닌지가 우리들로서 아는 것이 불가능하다고 말씀하시는 겁니까? 아마 그것은 알수 없겠지요....그러나 신은 알고 계실겁니다!"

이에 대한 브라우어의 대답은 다음과 같다.

"공교롭게도 나는 신과 연락하는 방법을 마침 갖고 있지 않습니다."

(요시나가 요시마사. 괴델 :불완전성 정리. 전파과학사 , 128쪽)

이 일화를 통해서 우리는 많은 것을 유추해 볼 수 있다. 브라우어는 수학을 무한의 영역으로 확장했을 때 발생하는 이러한 문제점 그리고 배리법에 의한 증명이 not A는 증명하여도 not not A는 증명할수 없다와 같은 이유 등을 내세워 배중률의 사용을 부정하거나 혹은 그것에 제한이 주어진다는 점을 강조한다. 반면 형식주의는 배중률이 비록 무한집합에 적용되었을 때에는 역설이 발생한다고 하여도 유한집합 내에서는 여전히 배중률이 유효하고 또 그것의 사용으로 인해 수많은 수학적 성과물을 성취할 수 있다는 점을 강조하였던 것이다.

그리고 직관주의는 수학적 지식이나 그 대상을 인간의 인식으로부터 독립적인 객관적인(objective) 것으로 보지 않고 인간정신의 구성적(constructive) 결과물로 간주한다는 점이다. 따라서 원주율에서 소수점이하 몇 번째자리에 9가 100번 연속되는지를 인간의 정신으로 구성적으로는 인식할 수 없기 때문에 그것이 몇 번째 자리수에 있는지 알려고 하는 시도는 수학적 연구의 대상으로는 무의미하다고 생각하는 것이고 위의 일화가 그 입장을 분명하게 보여준 것이다. 다시말하면 신만이 알 수 있는 것을 우리가 뭐하러 궁금해 해야 하는가라는 입장인 셈.

이런 입장은 사실 논리실증주의(Logical Positivism)의 입장과 유사하다. 논리실증주의도 참, 거짓을 증명할 수 없는 명제는 무의미하다는 것을 기조로 삼는다. 증명할 수 없는 가설이나 명제 예컨데 철학의 전통적인 형이상학적 담론이나 윤리학등이 그래서 무의미한 논의로 논리실증주의의 입장에서는 간주된다.  논리실증주의는 논리경험주의로도 불리우는데 이 때의  경험은 검증원리를 통해 참과 거짓을 증명할 수 있어야만 그 대상의 유의미성을 논할 수 있는 경험이다. 따라서 논리실증주의에서의 경험은 검증이전의 날것으로서의 가공되지 않은 경험이 아니라 "검증원리" 혹은 포퍼식의 "반증가능성"같은 논리적 잣대를 통해 참, 거짓이 확증될 수 있는 것이고 또 그럴 때에만 (가능한) 경험으로 인정될 수 있다는 입장을 취한다. 칼 포퍼(Karl Popper)가 그의 저서 <열린사회와 그 적들>에서 플라톤의 철학을 "반증불가능하다"는 이유로 비판하는 것도 결국 이런 맥락에서 이해할 수 있게 된다. (논리실증주의자/논리경험주의자들과 포퍼는 검증원리/귀납원리와 반증원리 간의 논쟁으로 그리고 포퍼와 쿤(Thomas Khun)은 반증원리와 공약불가능성(incommensurability), "혁명" 등으로 또 쿤과 이언 해킹(Ian Hacking)은 공약불가능성과 "실험과학"으로 대립한다. 이러한  논쟁은 여기서 정리해 보고자 하는 수리/수학철학의 범위를 벋어나는 '과학철학'의 영역이다. 이는 다른 기회에 한번 정리해 보도록 하겠다.) 

이와같이 논리실증주의는 수학에서의 직관주의와 많은 부분을 공유한다. 특히 그 인식의 구성적 관점만을 승인하고 인식주관 밖에 있는 객관적인 (수학적) 실재를 부정한다는 점에서 말이다. 그런데 브라우어가 자신의 이러한 입장을 직관주의(intuitionism)이라고 명명한 것은 칸트의 철학을 참조한 것인데 이것은 칸트철학에 대한 오독에서 비롯된다. (이에 대한 자세한 이야기는 다음번 페이퍼에서 다룰 것이다. )

반면 괴델은 직관주의가 비판하는 이러한 수학적 실재를 암묵적으로 가정하는 플라톤주의에 가깝다. 비록 형식적으로는 형식주의자이지만 내용적으로는 구성적 인식이 불가능한 영역이 실재한다고 보는 플라톤주의의 입장을 받아들임으로써 그는 형식주의에 대립하는 것이다. 이는 수학기초론내에서도 독특한 입장인 것으로 보인다. 비록 그가 불완전성 정리를 발표하기 위해 형식주의자의 수학적 방법을 동원하기는 했지만 결과적으로 "산술의 무모순성"이 불가능하다는 것을 형식적으로 "증명"함으로써 오히려 내용적으로는 그것에 대립하는 입장에 서게 된 점에서 말이다. 이는 다분히 이율배반적인 태도로 보인다. 어떻게 보면 그것은 의식으로부터 독립적인 실재를 가정하는 소박한 플라톤주의라고 하기보다는 "물자체"의 독립적 성격을 인정하면서도 그것의 경계에서 물자체를 간접적으로 인지하는 선험적이면서 초월적인 직관을 논하는 칸트철학과 맥락을 같이 하기 때문이다. 이러한 괴델의 입장을 플라톤주의라고 하기보다는 칸트주의라고 하면 지나친 표현일까? 
 

데카르트와 우주의 모양

지난번 페이퍼에 이어서 『데카르트의 비밀노트』에 나오는 이야기를 계속해 보자. 이번에 다룰 내용은 데카르트가 생전에 공개하지 않고 비밀리에 작성한 노트에 과연 어떤 내용이 있을까 하는 것이다.

 1650년, 데카르트가 스웨덴에 크리스티나 여왕의 개인교사로 건너갔다가 급작스런 독감증상으로(독살설도 존재한다. 그를 치료했던 의사가 위트레흐트논쟁으로 인해 데카르트를 극도로 혐오했던 네덜란드 사람이라고 한다)사망하자, 생전에 그가 기록했던 문서들은 당시 스웨덴주재 프랑스 대사였던 샤뉘를 통해 프랑스의 지인이었던 클로드 클레슬리에에게로 전해진다. 그 과정에서 배가 난파하여 데카르트의 노트를 소실할 뻔한 우여곡절을 겪기도 하였다. 어쨋든 운좋게도 문서를 손에 넣은 클레르슬리에는 데카르트의 노트들을 살펴보았는데 그 중에서도 온갖 알 수 없는 기호와 암호로 가득 차 있어서 도저히 해독할수없는 노트가 있었다. 그것이 문제의 비밀노트였다.

한편 당시 미적분문제로 씨름하고 있던 라이프니츠는 때마침 프랑스에 거주하고 있었고 동시대의 유명한 수학자였던 크리스티앙 호이겐스의 도움을 받아 데카르트의 유고에 대해서 이야기를 듣게 된다. 라이프니츠가 데카르트의 이 미발표 문서들에 관심을 가지게 된데에는 몇가지 이유가 있었다. 무엇보다도 당시 그가 연구하고 있었던 미적분이론과 큰 관련이 있다. 라이프니츠는 1673년 런던으로 건너가 영국 수학계 인사들과 교류를 하였고 왕립학회의 회원으로 선출되기도 하였다. 그런데 일부의 영국학자들은 그의 수학의 업적은 "데카르트로부터의 연역에 불과하다"고 폄하였다고 한다. 또한 "데카르트가 새로운 수학적 방법의 진정한 창시자였고 그의 후계자들의 공헌은 오직 데카르트의 연장이며 상세화일 뿐이다."라고 주장하는 편지를 받기도 하였던 것이다. 이에 미적분이론과 같은 새로운 수학이론을 고안하고 있던 라이프니츠는 데카르트가 남겼다고 하는 미발표 유고들 속에 혹시라도 자신이 발표하려고하는 수학이론과 비슷한 것이 있지 않았나하는 확인 작업이 꼭 필요하였다. 혹시라도 자신이 미적분 이론을 발표한 이후 데카르트의 유고가 출판되어 자신의 독창적 이론이 의심받게 된다면 그것이야 말로 큰 낭패가 아닐 수 없었던 것이다. 가뜩이나 영국수학자들로부터 데카르트의 후계자에 불과하다라는 평가를 듣고 있던 마당에.때 마침 데카르트의 비공개 노트에 대해서 듣게 된 그는 부랴부랴 호이헨스의 소개를 통해서 클레르슬리에가 보관하고 있었던 데카르트의 유고를 확인하게 되었다. 그 때가 1676년 7월이었다.

라이프니츠가 보았던 데카르트의 사라진 "비밀노트"의 제목은 <입체의 요소에 관하여>였다. 노트는 모두 16쪽이었다고 한다. 노트는 도형그림이 한쪽에 빽빽하게 그려져 있었고 온갖 상징들과 암호들로 이루어져 있었다. 그러나 라이프니츠는 암호해독의 전문가였다. 또한 장미십자회 회원이었으므로 장미십자회 회원들이 사용하는 상징의 의미를 누구보다도 잘 파악할 수 있었다. 라이프니츠야 말로 데카르트의 비밀노트를 가장 잘 해독할 수 있는 적임자 였던 것이다. 필사를 하다가 그는 중간에서 멈추었다고 한다. 왜냐하면 시간도 촉박했을 뿐더러 그 노트의 핵심내용을 이미 간파 했으므로. 대신 그는 짤막한 주석을 남겼다. 그런데 그 주석이 완벽하게 이해되기 까지는 또다시 300년이 걸렸다. 그 주석의 해독은 1987년 프랑스 출신 수학자인 피에르 코스타벨에 의해서 비로소 완성된다.

그렇다면 데카르트는 왜 정다면체에 그렇게 관심이 있었을까? 비밀노트를 작성하면서까지 숨기려고 했던 비밀은 무엇이었을까? 유클리드의 『기하학 원론』은 총 13권으로 이루어져 있다. 그중 마지막 13권째는 정다면체에 관한 내용으로 이루어져 있다.  그것은 플라톤이 중요하게 다루어서 플라톤입체라고도 불리우는데 그 5개의 플라톤 입체는 1. 정사면체, 2. 정육면체, 3.정팔면체, 4, 정십이면체, 5. 정이십면체이다.





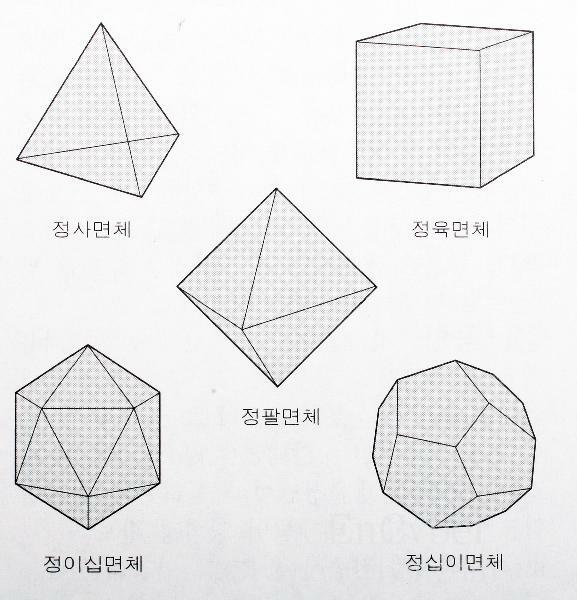
정다면체는 각 면이 정삼각형, 정사각형, 정오각형으로 이루어져 있고 그 면들이 모두 합동인 입체도형이다. 그런데 이 정다면체의 중요한 특징이 "정다면체가 구에 내접한다"는 사실이다. 유클리드의 『기하학원론』에서는 이것을  여러가지 정리로 증명한다. 정다면체가 구에 내접한다는 것은 예를 들어 정육면체를 구에 넣으면 구에 쏙 들어가고 그 여덟개의 모서리가 모두 구에 내접한다는 것인데 이 성질은 앞서 말한 5개의 정다면체 모두에 해당한다. 이러한 정다면체의 성질은 고대 이집트에서도 알려져 있었고 고대그리스에서도 매우 중요한 성질로 "그리스기하학의 결정판이며 그리스 기하학의 3차원적 확장"이고 "우주의 비밀"을 담고 있다고 생각했다.  

 

데카르트는 이러한 정다면체에 공통으로 존재하는 원리가 무엇인지 연구하였다. 그가 이처럼 정다면체 속에 숨어있는 성질을 연구하였던 것은 앞에서 이야기 한것처럼 정다면체속에 우주의 숨겨진 비밀이 있을 것이라고 믿었기 때문이다. 그가 이런 정다면체 기하학에 관심을 기울인데에는 당시 지식인들 사이에 존재하였던 신비주의사상과  케플러와 같은 천문학자의 영향이 컷던 것으로 보인다.





데카르트보다 먼저 우주의 구조를 연구했던 케플러는 1596년에 발표한『우주구조의 신비 Prodromus Dissertationum Mathematicarum Continens Mysterium Cosmographicum』 라는 책에서 코페르니쿠스의 『천체의 회전에 관하여』에서 서술된 지동설을 지지하는 이유를 기하학적 모델을 동원하여 밝힌 바 있다. 그는 이 책에서 태양계의 행성들은 태양주위를 원의 궤도로 공전하는데 그 공전의 모델을 바로 이 정다면체의 성질을 이용하여 설명하였다. 당시까지 발견되었던 6개의 행성 즉 수성, 금성, 지구, 화성, 목성, 토성을 정다면체를 내접, 외접하는 6개의 구와 연관시켜 설명하였던 것이다.







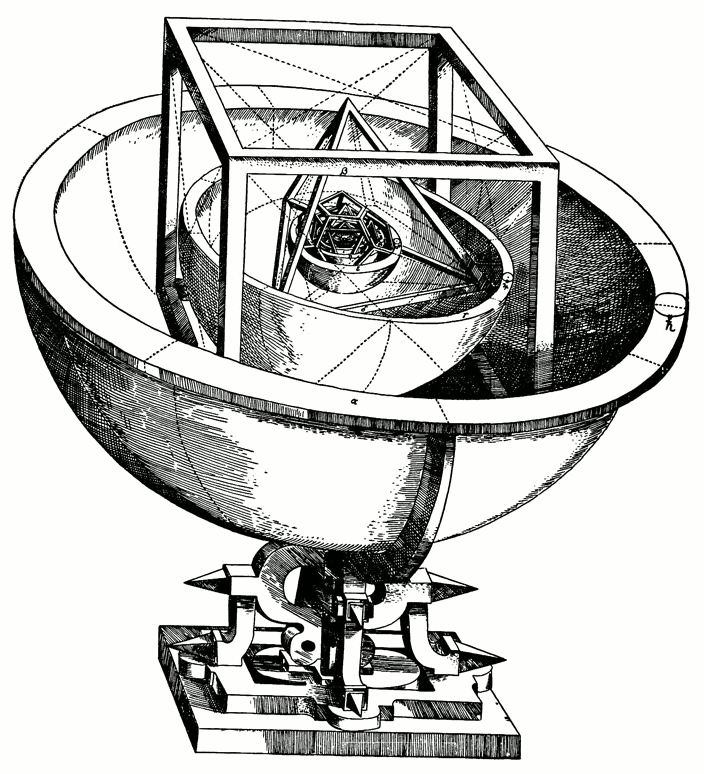
이처럼 그가 정다면체의 성질을 이용해 우주의 구조를 밝히려 했던 것은 분명 피타고라스와 유클리드 이래로 그리스기하학에 이어져 내려온 기하학을 통해 우주의 비밀을 밝히려고한 시도의 결과였다. 비록 그는 후에 티코 브라헤의 조수로 있으면서  좀더 정밀한 관측을 통해 후대에 케플러의 법칙으로 명명된 3개의 법칙을 발표하면서 태양계 행성의 궤도는 원이 아니라 타원이라는 것을 밝혀내기는 했지만 타원 역시 기하학의 원리에 의해서 유도되는 도형이 아닌가.

 



그런데 사실 이러한 케플러의 우주관은 그만의 독창적인 생각이 아니다. 그는 당시 유럽의 지식인들 사이에 유행했던 헤르메스주의와 같은 신비주의사상에 깊은 관심이 있었는데 특히 니콜라우스 쿠사누스Nicolaus Cusanus와 같은 학자에 깊은 관심을 가졌다고 한다. 쿠사누스는 에른스트 카시러에 의하면 "르네상스 철학을 하나의 체계적인 통일로 파악하려는 모든 고찰은 그 출발점을 쿠사누스에게 두어야 한다."와 같은 평가를 받는 인물이다. 그의 글을  인용해 보자.





"그것이 땅이든 공기든 불이든 다른 무엇이든 간에, 그것들이 우주의 고정된, 움직이지 않는 중심에 존재하는 것은 불가능하다.(...)따라서 중심일 수 없는 지구가 어떤 운동도 하지 않는다는 것은 있을 수 없다.(...)지구가 세계의 중심이 아닌 것처럼, 모든 항성 천구는 세계를 감싸는 둘레가 아니다. (...)이런 사실들로부터 지구가 운동하는 것은 자명해진다." (과학의 탄생. 동아시아, 303쪽에서 재인용)

이러한 부동의 고정점으로서의 지구를 부정하는 것은 그때까지의 전통적인 우주관이었던 아리스토텔레스적 우주관을 부정하는 것이었다.한편 그는 신의 창조물인 우주 속에는 수에 의해서 표현되는 비례의 법칙이 숨어있다고 이야기한다. 

"수가 없으면 존재하는 것끼리의 다(수)성은 존재할수 없다. 왜냐하면 수가 없어지면 사물의 구별, 질서, 비율, 조화, 나아가 존재하는 것끼리의 다성 자체가 없어져버리기 때문이다.(과학의 탄생. 동아시아, 307쪽에서 재인용)    

"신은 세계를 창조할 때 산술학, 기하학, 음악 및 천문학을 동시에 사용했다. 그래서 우리도 모든 사물이나 모든 원소, 모든 운동의 비율적인 관계를 탐구할 때 이들 학술을 사용한다." (지혜로운 무지 De Docta Ignorantia. 과학의 탄생, 동아시아, 308에서 재인용)





이처럼 쿠사누스는 우주의 구조를 해명하기 위해서 지구의 운동가능성과 그속에 숨어있는 비례와 조화의 법칙을 이해하기 위한 수학의 필요성을 강조하여 후대에 코페르니쿠스나 케플러 그리고 데카르트와 라이프니츠와 같은 근대적 학자에게 큰 영향을 끼쳤던 것이다.(사실 이러한 쿠사누스의 우주관자체도  플로티누스Plotinus의 일자의 철학와 같은 신플라톤주의의 영향을 받은 것으로 볼 수 있으나 이글에서는 그와 관련된 논의는 생략하기로 한다.) 


이와같은 당시 유럽에 존재하였던 신비주의적 전통은 케플러와 데카르트에게도 강하게 작용했음에 틀림없다. 그리고 케플러와 동시대 인물이면서 그를 생전에 만났음이 틀림없고 신비주의 비밀결사였던 장미십자회 소속 학자인 요한 파울바허와 같은 학자와 교류하면서 그들의 영향을 받은 데카르트는 그리스 기하학 중에서도 우주의 비밀스러운 구조와 관련이 깊은 것으로 보이는 정다면체 기하학의 신비로운 성질에 더욱 매료될 수밖에 없었던 것이다.  그렇다면 라이프니츠가 데카르트의 비밀노트에서 밝혀낸 것은 과연 무엇일까?

라이프니츠는 데카르트의 비밀노트를 필사하는 도중 수수께끼같은 수열을 보게 된다.

4  6  8  12  20 그리고 4  8  6  20  12     

그는 첫번째 수열의 의미를 금방 파악했다. 그것은 앞에서 말한 정다면체의 면의 수였던 것이다. 즉 4(정사면체), 6(정육면체), 8(정팔면체), 12(정십이면체), 20(정이십면체)를 의미하였던 것. 그리고 두 번째 수열은 각각의 꼭지점의 수와 일치한다. 여기에 모서리의 수를 추가하면 다음과 같은 수열을 얻을 수 있다.

         정사면체      정육면체      정팔면체       정십이면체        정이십면체

   면       4              6               8               12                   20

꼭지점     4               8              6               20                   12

모서리     6               12            12               30                  30

그런데 여기에서 면과 꼭지점의 수를 더한다음 모서리의 개수를 빼면 2가 나온다. 면을 F라 하고 꼭지점을 V 모서리를 E라고 하면

F + V - E = 2

이 공식은 위의 5가지 다면체 모두에 적용될 수 있다. 예컨대 정사면체의 경우 4+4-6=2, 정육면체도 6+8-12=2이고 나머지도 모두 같은 결과가 나온다는 것을 알 수 있다. 이러한 성질은 후에 위상불변량(topological invariant)라고 불리게 되는 성질을 보여주는 공식이 되는데 데카르트가 발견한 이 공식은 후에 위상수학(topology)라고 불리우는 수학의 분야에서 발견한 최초의 정리로 알려지게 된다.

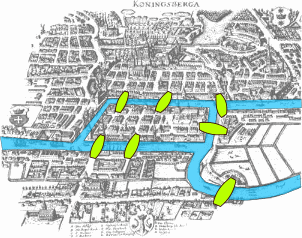
위상수학은 라이브니츠에 의해서 최초로 그 가능성이 예견된 것으로 알려졌다. 그는 1679년 호이겐스에게 보낸 편지에서 "대수학이 양을 다루는데 비해 직접 위치의 기하학(geometra situs)을 다루는 해석의 또 다른 분과가 필요할 것이다."라고 말했다고 한다.

1732년 레온하르트 오일러Leonhard Euler는 그 유명한 "쾨니히스베르크의 다리문제"를 다루면서 "(쾨니히스베르크의 다리문제같은 것 들이) 아마도 라이프니츠의 위치의 기하학의 문제일 것이다."라고 말하였다. 또 그는 위에서 언급한 데카르트의 공식을 발견하여 "다면체 공식"를 발표하기도 한다. 그러나 사실 그 정리는 오일러보다 데카르트가 먼저 발견하였던 것이다. 최근에는 그 공식을 피에르코스타벨의 재발견 이후에는 "데카르트-오일러 공식"으로 부르는 경우도 많다고 한다.  

그런데 이러한 "데카르트-오일러 공식"이 우주의 비밀을 밝히는 것과는 도대체 무슨 관련이 있는 것일까? 앞에서 이야기 했듯이 그것은 위상수학에서의 위상불변량(topological invariant)을 나타내는 공식이다. 그런데 이 위상불변량은 위상적 속성topological property라고 불리우기도 하는데 위상수학에서의 위상동형사상(homeomorphism)과 관련이 있다. 위상동형이란 무엇인가? 다음 글을 확인해 보자.

"오일러의 공식(F+V-E=2)에서 유의할 점은 이것이 꼭지점 모서리 면의 개수에 관한 것일 뿐, 모서리의 길이나 면의 꼴과 면적에는 아무 영향을 받지 않는다는 것이다. 즉, 주어진 모서리가 곡선을 이루고 주어진 면이 곡면이어도 마찬가지 결과를 얻는다. 프왕카레의 관찰에 따르면, 볼록다면체의 표면을 연속적으로 변형하여 구의 표면으로 보아도 역시 공식이 성립한다.(...)두 점집합 A, B에 대하여 1대 1대응 f : A → B가 있어 f 도 연속이고,역으로 역대응도 연속이라 하자. 여기에서 f 와 그것의 역대응(함수)가 연속이라 함은 A에서 서로 가까이 있는 점들은 f 에 의하여 B의 서로 가까운 점들로 변환되고 역으로 B의 서로 가까운 점들은 f 의 역함수에 의하여 A의 가까운 점들로 변환된다는 뜻이다.(...)이와 같은 성질을 만족하는 변환(함수) f 를 위상동형(homeomorphism)이라고 말하며 이 같은 f 에 의해서 불변인 성질을 위상적 성질(topological property)라고 부르는 것이다."(수학의 세계. 박세희. 서울대학교출판부, 171∼2쪽)

다시말하면 함수 f 가 일대일 대응이고 그것의 역함수도 성립하며 또 연속continuity라면 그것에 의해 표현되는 기하학적 속성들은 같은 위상적 성질을 가진다는 이야기이다. 위상수학에 대해서 이야기할때 흔히들 이런 농담을 한다고 한다. "수학자들은 도우넛과 머그잔을 구별하지 못한다." 그 이유는 위상수학으로 보았을 때 도우넛의 표면 (토러스 torus)와 머그잔의 표면은 위상동형이기 때문이다. 마찬가지로 구의 표면과 (정)다면체는 위상동형인데 데카르트가 비밀노트에 적었던 내용이 바로 이 구와 다면체의 동형성에 관한 위상불변량공식이었던 것이다. 

  

그런데 우리가 살고있는 우주는 어떤 모양일까? 우주의 크기는 유한할까? 무한할까? 다시말해서 우주에는 경계boundary가 있을까? 대부분의 수학자들 특히 위상수학을 공부하는 학자들은 우주는 유한하다고 말한다. 우주를 예를 들어 3차원으로 된 정육면체 지도로 우주의 부분들을 표현한다면 유한한 갯수의 지도의 합으로 모두 표현할 수 있다고 한다. 그것을 수학용어로는 컴팩트(compact)하다고 한다. 이것이 의미하는 것은 결국 우주의 크기는 무한한 것이 아니라 유한하다는 것. 그런데 여기서 주의해야 할 것은 우주의 크기가 유한하다고 해서 우주의 경계boundary가 있다는 말은 아니라는 것이다. 크기는 유한한데 경계가 없다는 말은 무엇일까?

2차원 표면에 그릴 수 있는 둥그런 원반을 생각해 보자. 그것의 경계는 원이다. 원반의 내부는 2차원이지만 경계는 그것보다 한 차원 낮은 1차원의 원인 셈. 우리가 만약 이 원반 내부의 한 지점에서 바깥쪽으로 계속 걸어나가면 결국에는 1차원으로된 원 즉 경계를 만나게 된다. 그런데 구면sphere의 경우는 어떨까? 구면은 크기는 유한하지만 경계는 없다. 예를들어 우리가 살고있는 지구를 생각해 보자. 우리가 지금 있는 자리에서 출발하여 일직선으로 똑바로 계속 나아간다면 어떻게 되는가? 과거에 지구는 둥그렇지 않고 평평하다고 생각했던 적이 있다. 이 시절에는 지구의 끝 즉 경계에 다다르게 되면 거대한 낭떠러지나 절벽같은 것이 있을 것이라고 상상했다. 그런데 사실 지구의 표면은 오늘날 알다시피 구면sphere이다. 때문에 결국 그 사람은 자기가 출발한 자리로 되돌아 올 수밖에 없게 된다. 만약 지구에 경계가 있다면 우리는 원이나 직선과 같은 한 차원 낮은 경계와 만나야 하는데 그런 경계는 나오지 않고 자기가 출발한 자리로 되돌아오는 결과가 되는 것이다. 이 사실은 지구와 같은 구면은 경계가 없다는 것이 된다. 다시 정리해서 말하자면 원반과 같은 도형은 유한하고(compact하고) 경계boundary가 있지만, 지구의 표면과 같은 구면은 유한하지만 경계는 없다는 것이다. 그런데 수학자들은 우주의 모양도 이처럼 유한하지만 경계는 없는 즉 구면과 같은 성질을 가지고 있다고 생각한다. 왜 그렇게 생각하게 되었을까?

우리는 지구가 둥글다는 것을 안다. 그것을 알 수 있는 이유는 우리가 지구의 밖을 볼수있기 때문이다. 그리고 가장 확실하게는 지구밖에 나가서 지구를 볼 수 있기 때문. 우리는 그것의 움직일 수 없는 증거를 지구 밖에서 우주선이 지구의 모습을 촬영해 오면서 확인 할수 있었다. 그런데 우리는 우주의 밖으로 나갈수 없다. 아니 우주의 크기가 정확히 얼마나 되는지도 모른다. 그러니 우주의 밖으로 나가서 우주의 모양을 확인하는 것은 불가능한 일이다. 그렇다면 우리는 어떻게 우주의 모양을 가늠해 볼 수 있을까? 한 가지 방법은 우주의 모양에 관해서 위상학적 성질topological property을 확인해 보는 것이다.

 

수학의 밀레니엄 문제 중 하나인 푸앵카레의 추측(Poincaré conjecture )은 바로 이 위상수학 그리고 우주의 모양과 관련된 수학문제이다. 푸앵카레의 추측은 위상수학이 이룬 최고의 성과인 동시에 수학의 밀레니엄 문제로서 수많은 수학자들이 이의 증명을 위해 노력을 해왔다. 그 내용은 다음과 같다.

"밀폐된 3차원 공간에서 모든 밀폐된 곡선이 수축되어 하나의 점이 될 수 있다면, 이 공간은 반드시 원구로 변형될 수 있다”

이와 관련된 설명 하나를 인용해 보자.

"만약 사과표면의 둘레에 고무줄을 감는다면 우리는 그것을 천천히 이동시킴으로써 찟거나 표면으로부터 떨어뜨리거나 할 필요없이  한 점으로 수축시킬 수 있다. 반면 같은 고무줄을 도넛의 주위에 적절한 방향으로 늘어뜨린다면 고무줄이나 도넛을 자르지 않고서는 한 점으로 수축시킬 수 없다. 우리는 사과의 표면은 “단순히 연결되어 있다 simply connected”라고 말한다. 그러나 도넛의 표면은 그렇지 않다. 푸앵카레는 거의 한세기전 2차원 구면은 이러한 단순연결성simple connectivity의 성질을 기본적인 특징으로 한다는 것을 알았다. 그리고 3차원 구면(최초의 지점origin으로부터 단위거리unit distance에 있는 4차원 공간에서의 점들의 집합)에 대응하는 질문을 제기했다. 이 질문은 매우 어려운 것으로 드러났고 수학자들은 그 이후로 (이 문제를 해결하기 위해) 노력했다. "

If we stretch a rubber band around the surface of an apple, then we can shrink it down to a point by moving it slowly, without tearing it and without allowing it to leave the surface. On the other hand, if we imagine that the same rubber band has somehow been stretched in the appropriate direction around  a doughnut, then there is no way of shrinking it to a point without breaking either the rubber band or the doughnut. We say the surface of the apple is "simply connected," but that the surface of the doughnut is not. Poincare almost a hundred years ago, knew that a two dimensional sphere is essentially characterized by this property of simple connectivity, and asked the corresponding question for the three dimensional sphere (the set of points in four dimensional space at unit distance from the origin). This question turned out to be extraordinarily difficult, and mathematicians have been struggling with it ever since.

 이를 다시 쉽게 설명해보면 다음과 같다. 우리가 만약 구면에 고무줄과 같은 닫힌 고리loop를 건다고 생각해 보자. 그러면 우리는 그 고리를 구면의 어떠한 위치에 걸더라도 고무줄이나 구면을 자를 필요없이 한 점으로 수축시킬 수 있다. 얼핏 그다지 특이할 것도 없는 이 사실은 위상수학적으로 하나의 위상적 성질topological property을 표현하는 성질이다. 그런데 그렇지 않은 도형이 있다. 바로 도넛의 표면 즉 토러스 torus이다.

위의 이미지를 보면 알겠지만 저 토러스의 원환면에 고무줄을 건다면 우리는 그것을 한 점으로 수축시킬 수 없다. 그러기 위해서는 토러스를 자르거나 고무줄을 잘라야 한다. 이것은 매우 중요한 차이이다. 따라서 위상수학에서는 구면처럼 고리와 같은 폐곡선을 절단하지 않고 한 점으로 수축시킬수 있는 것을 단순히 연결되어 있다 simply connected고 규정하고 토러스와 구별하고 있는 것이다.

그런데 문제는 우리가 쉽게 도식화할 수 있는 2차원 다양체인 구면과 토러스와는 달리 우주는 3차원 다양체 3-dimensional manifold라는 사실이다. 3차원 다양체는 2차원 다양체의 특정한 점(집합)을 일대일 대응시키면서  연결한 것이다. 때문에 이것은 도식화시키기도 어렵고 계산하기도 매우 까다롭다. 그런데 푸앵카레는 이 3차원 다양체의 모양을 가진 우주도 2차원 다양체인 구면과 같은 단순연결성을 가진다고 추측했던 것이다. 그것이 푸앵카레의 추측Poincaré conjecture 이다.

그런데 그것의 수학적 증명은 푸앵카레가 최초로 추측을 제기한 이후 약 100년이 걸렸다. 그 증명을 최초로 해낸 사람이 바로 그리고리 페렐만 Grigori Perelman이다. 페렐만은 푸앵카레 추측과 관련된 논문을 2002년 최초로 인터넷(www.arXiv.org)에 올렸다. 그리고 그 뒤 두 편의 논문을 더 추가한다. 페렐만이 주로 사용한 수학공식은  리처드 해밀턴 Richard Hamilton이 리만 메트릭을 가진 다양체를 해석학적으로 해명하기 위해 사용한 리치 흐름 방정식이었다.  (자세한 설명은 이곳을 참조: http://en.wikipedia.org/wiki/Grigori_Perelman )

이를 이용해 그는 푸앵카레 사후 100년동안 증명되지 못한, 그리고 클레이 수학연구소(www.claymath.org)  가 수학의 7대 난제로 선정하고 이것을 증명한 사람에게 100만 달러의 상금을 걸었던 그 문제를 증명하였던 것이다. (페렐만의 증명을 직접 보려면 이곳을 참조: http://arxiv.org/abs/math.DG/0211159 ) 이 증명의 발표이후 여러 검토작업이 있었지만 2006년 사실상 최종적으로 증명이 완료된 것으로 공인된다. 이 업적으로 페렐만은 2006년 수학계의 노벨상이라는 필드상 fields medal 수상자로 선정되었지만 그는 수상을 거부하였다.(필드상 위원회에서는 페렐만이 수상을 거부하리라는 것을 알면서도 그를 수상자로 선정했다고 한다.) 많은 수학자들은 페렐만의 이 푸앵카레 추측의 증명은 수학의 역사에서 기념비적 사건이며 앤드류 와일즈 Andrew Wiles 가 증명에 성공했던 페르마의 정리에 상응하는 아니 어쩌면 그것보다도 더 중요한 증명일지 모른다고 평가한다. 이런 평가가 결코 과장이 아닌 것이 푸앵카레의 추측은 단순히 특정 수학의 정리를 증명하는 문제에 그치는 것이 아니라 바로 우주의 구조와 비밀의 해명이라는 문제와 연관되기 때문이다. 이는 지금까지의 인류의 역사에서 수많은 철학자, 물리학자, 수학자 혹은 성직자들이 해명하려고 노력해 왔던 그런 주제이다. 더불어 데카르트도 그의 비밀노트에 아무에게도 공개하지 않고 작성해 왔던 바로 그 주제였던 것이다. 이렇게 해서 데카르트의 비밀노트로부터 시작된 우주의 모양에 대한 수학적 해명이 페렐만을 통해서 하나의 큰 도약을 완성하게 된다.

그런데 페렐만은 클레이 수학연구소가 상금으로 걸었던 100만달러와 필드상을 모두 거부하였다. 그리고 현재 러시아에 은둔하면서 언론과의 접촉을 피하고 살고있다고 한다. 타고난 성격때문인지 어떤지는 모르지만 혹시 그도 데카르트처럼 비밀리에 작성하고 있는 노트가 있는 것은 아닐까? 앞서서 그가 발표한 푸앵카레 추측의 증명보다 훨씬 더 놀랍고 충격적인 어떤 우주의 비밀을 밝혀줄 그런 비밀노트를. 그래서 그것을 아직까지는 세상에 공개하기 싫어서 은둔하면서 살고 있는 것은 아닐까?

P.S. 푸앵카레의 추측과 관련해서는 『데카르트의 비밀노트』와 공교롭게도 비슷한 시기에 출판된 『푸앵카레의 추측 - 우주의 모양을 찾아서 』를 참고하면 도움이 되겠다. 수학적 설명은 최소화한 책이긴 하지만 설명이 그다지 쉽게 다가오지는 않는다. 하긴 이미지로 도식화시키기도 쉽지 않은 3-다면체를 말로서 설명하려니 그게 그리 간단하지는 않았을 것이다.