조제프 라그랑주
Joseph Louis Lagrange
두산백과
프랑스의 수학자 ·천문학자. 그가 해명한 해석역학은, 그때까지 발전한 해석학을 역학에 응용한 것이며, 그의 저서 《해석역학》에 의해, 역학은 하나의 새로운 발전의 단계로 들어서게 되었다. 그 외에 정수론·타원함수론·불변식론(不變式論) 등에 관해 많은 연구 업적이 있다.
....
그가 해명한 해석역학은, I.뉴턴의 미적분에 의한 운동방정식이 확립된 후 100년만의 일로, 그때까지 발전한 해석학을 역학에 응용한 것이며, 그의 저서 《해석역학》(1788)에 의해, 역학은 하나의 새로운 발전의 단계로 들어서게 되었다.
라그랑주의 해석역학에 의한 운동방정식은 뉴턴의 방법에 비해 보다 일반적으로 운동의 미분방정식을 유도할 수 있다. 대수(代數)에 있어서의 그의 일반화 방향은 5차 이상의 대수방정식 해법에 대한 연구로서, 이 연구는 근(根)의 치환군(置換群)에 착안한 것으로, N.H.아벨과 E.갈루아의 업적의 선구자 역할을 한 것이다.
라그랑주 점
Lagrangian point
두산백과
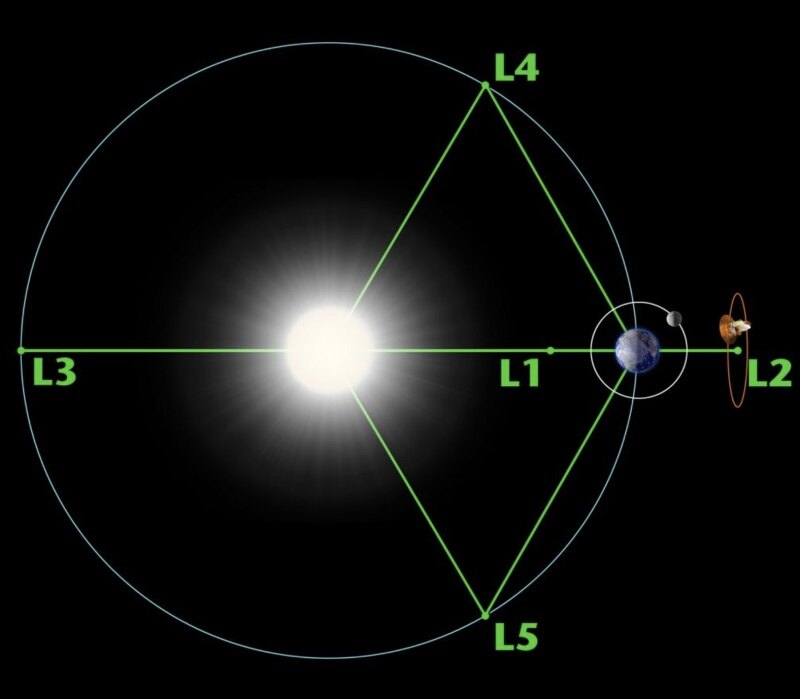
케플러운동을 하는 두 천체가 있을 때, 그 주위에서 중력이 0이 되는 5개의 점으로 라그랑주 특수해라고도 부른다. 두 천체를 잇는 직선상에 3개, 두 천체와 정삼각형을 이루는 2개의 점이 있다. 그 중에서도 삼각형을 이루는 2점에 제3천체가 있을 경우 매우 안정하여 라그랑주 점이라고 부른다.
본문
라그랑주는 케플러운동을 하고 있는 두 천체를 연결하는 직선상의 3점과, 또 두 천체와 정삼각형을 이루는 2점에서 중력이 0이 된다는 것을 발견하였다. 이 5개 점을 라그랑주의 특수해라고 한다. 또한, 삼체문제(三體問題)는 일반적으로 그 해를 구할 수 없지만, 라그랑주는 특수한 예로서, 제3의 천체의 질량을 무시할 수 있을 경우, 제3천체는 라그랑주의 특수해 중 삼각형을 이루는 2점에 있을 때 매우 안정하다는 것을 증명하였다. 이 2점을 특별히 라그랑주 점이라고 한다. 실제로 목성의 궤도 위를 목성과 함께 도는 트로이 소행성군은 그 위치가 태양과 목성이 정삼각형을 이루는 곳임이 확인되었다. 이에 비해 직선상의 3점은 로슈한계 위의 점으로서 역학적으로 다소 불안정한 점이라는 것이 밝혀졌다
[칼럼 : 칼럼 | 제임스웹 우주망원경, 그리고 라그랑주 포인트 ]
지구와 태양의 중력이 균형을 이룬 지점을 라그장주 포인트라고 한다. 위 그림에서는 L2궤도를 말한다. 이 궤도서 지구와 태양을 바라보면 두 물체가 늘 같은 위치에서 보이게 된다고 한다. 이 위치에 망원경을 배치하면 지구나 태양에 가려지지 않아 방해받지 않고 우주를 관측할 수 있다. 또한 중력이 균형을 이룬 지점이기 때문에 궤도를 유지하기 위한 연료사용도 최소화할 수 있다.
지구와 달, 지구와 태양, 태양과 목성 등 각각의 천체 사이에는 각각의 라그랑주 포인트가 존재한다. 두 천체 간의 라그랑주 포인트는 총 5개로, 라그랑주 포인트의 앞글자 L에 번호를 붙여 L1~L5라고 부른다. 지구와 태양 간의 라그랑주 포인트는 지구(earth)의 앞글자를 붙여 EL, 지구와 달 간의 라그랑주 포인트는 달(lunar)의 앞글자를 더해 LL이라고 표현하기도 한다. 지구와 태양 간에 위치한 라그랑주 포인트 중에 지구에서 가장 가까운 L1(EL1) 지점은 지구에서 태양 방향으로 약 150만㎞ 떨어져 있다. 지구와 달 사이 거리(38만㎞)보다 약 4배 정도 멀다.
(출처 : https://m.blog.naver.com/anni13/222835835451)