-

-
10개의 특강으로 끝내는 수학의 기본 원리
제리 킹 지음, 박영훈 옮김 / 동아엠앤비 / 2017년 7월
평점 :



작년 말, 나는 갑자기 수학을 공부하고 싶어졌다. 왜 갑자기 그런 생각이 들었을까? 당시 내가 초등학생을 위한 수학 과목 서비스를 기획하고 있었기 때문은 아니었던 것 같다. 물론 그게 작은 계기가 됐을 수는 있지만, 거기엔 보다 큰 뭔가 근본적인 갈증이 있었던 것 같다. 이를테면, 세상의 본질이 궁금했달까?
우리는 실생활에서 다양한 현상을 마주하지만 그런것들을 만들어내고 조정하는 추상적 법칙이 어딘가에 내재되어 있다고 생각하는 것 같다. 그래서 생각이라는 것이 탄생한 이래 수많은 철학자들이 그 본질을 찾아내려 한 것이다. 그 중 가장 유명한 후보는 역시 '수'일 것이다. 그리고 수는 지금까지도 꽤 설득력 있는 의견을 제시한다. 그렇다면 수는 정말로 우리 세계의 본질일까? 이런 생각을 처음으로 가진 피타고라스는 그렇다고 말한다. 그와 그의 제자들에게 수는 일종의 종교였다. 그들에게 수학자는 수학이라는 종교가 만들어 놓은 법칙을 이해하고 해석하는 사제였고, 신은 최초의 수학자였다.
수학을 공부하고자 하는 두 번째 이유는 하나의 거대한 체계가 무엇을 기반으로 어떻게 형성됐는지 궁금했기 때문이다. 나는 쌓고 만드는 걸 좋아하는 사람이고 그걸 업으로 삼고 있기도 하다. 그러니 쌓을 땐 무엇을 조심해야하고 쌓고나면 뭘 확인해야 하는지, 역사적으로 가장 오래되고 방대한 체계를 참고하는 게 당연한 일 아니겠는가.
수학의 증명 과정을 보고 있으면 그걸 종교로 받아들인 피타고라스의 심경이 이해가 된다. 하나의 증명을 위해 수학은 더 이상 증명이 불가한 자명한 사실만을 이용한다. 깍아내고 깍아내고 또 깍아내어 손에 든 정수. 그래서 수학은 절대 복잡하지 않다. 우리가 수학을 어렵다고 생각하는 이유는 우리의 수학 교육이 증명없이 공식을 들이밀기 때문이다. 증명 과정을 알고 있으면 결과(공식)는 자연스럽게 도출 될 수 있다. 그러나 결과만을 주입하면 그 과정을 파악하는 건 괴로운 연구 과제가 된다. 우리는 이 순서를 바꿔서 해왔기 때문에 수학을 지긋지긋해 하는 것이다.
물론 수학에서도 계명은 존재한다. 유대인들이 십계명에 어떠한 토도 달지 않듯 그렇게 믿어야만 하는 명제는 존재하는 것이다. 예컨대 "0으로 나누지 말지어라" 같은. 물론 저자는 이를 증명하기 위해 아래와 같은 계산을 시도한다.
x, y를 0이 아닌 유리수라고 하고 x=y라고 하자. 그러면 다음이 성립한다.
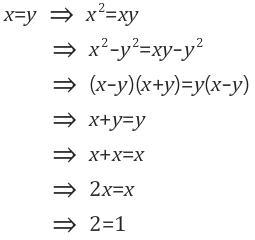
2x=x를 만족하는 유리수는 x는 0이 유일하다. x가 0이 아니라면 우리는 2x=x 의 각 항을 x로 나눌 수 있기 때문에 2=1이라는 결과를 받아들여야 한다. 이는 모순이므로 그 무엇도 0으로 나눌수는 없다. 그러나 나는 여기에 뭔가 석연치 않음을 느낀다. 증명 과정에서 우리는 증명되지 않은 어떠한 방법도 사용하지 않았다. 그런데도 불구하고 2=1이라는 결과가 나왔다면 1과 2를 구분하는 우리의 셈 체계에 근본적 결함이 있다는 말 아닐까? 다음은 1과 0.999...(9가 무한히 반복된다)가 같음을 증명하는 과정이다.

수학적으로 9가 무한히 반복되는 실수 0.999...는 정확하게 1이며 이는 결코 어림한 값이 아니다. 위 수식이 바로 이 사실을 증명하고 있다. 그렇다면 왜 2=1은 모순이고 1=0.999...는 모순이 아닐까? 이는 그저 9가 무한히 반복되는 실수 0.999...를 0.999...로 표현할 수 밖에 없는 우리 문자 체계의 한계로 봐야하는걸까? 이를 대수롭지 않게 생각하는 사람들도 있겠지만 수학의 입장에서 이는 아주 치명적인 문제다. 수학은 수 많은 명제가 동시 다발적으로 생성되어 구성한 체계가 아니라 아주 당연한 정리부터 하나씩 차곡 차곡 쌓아 올려 만든 학문이기 때문이다. 따라서 그 중 하나라도 결함이 존재한다면 그 증명을 기반으로 만들어진 이후 증명들은 모두 믿을 수 없는 것이 되버린다. 예컨대 1과 2는 아무런 차이가 없음을 증명할 수 있다면 지금껏 수학이 아무리 훌륭한 성과를 냈고, 아무리 현실 세계의 현상과 부합한다 하더라도 송두리째 무너질 수 밖에 없다. 나는 왜 모든 수학자들이 신경과민에 빠지지 않는지 신기하다.
물론 여기에 대한 답을 얻지는 못했지만 나는 이 책을 통해 꽤 즐거운 여행을 했다. 일반적으로 수학은 간결하고, 아름다우며, 우아하기까지 하다. 증명 과정을 보고 있으면 그 신묘함에 저절로 고개가 수그려진다. 그러나 이 책은 수학에 대한 책이라기 보다는 수학책에 가깝다. 아름답고 우아하다는 말에 이끌려 덥석 집어든다면 갈수록 복잡해지는(왜 앞 단원을 놓치면 줄줄이 망하는지 알겠다) 증명과 용어에 비명을 지를지도 모른다.
이 책을 읽으며 놀라웠던 건 각 장의 순서가 우리 수학 교육의 순서와 크게 다르지 않았다는 것이다(그 끔찍한 수학의 정석과 아주 흡사하다). 그러니 우리는 잘못된 내용을 배운 건 아니다. 단지 잘못된 전달 방법으로 고통받은 것 뿐. 내가 배우던 시절에도 이렇게 원리를 강조하는 교수법이 있었다면 훨씬 즐거웠을 것 같다. 하지만 이를 실천하는 선생님들은 시험에 나오는 문제를 풀어달라는 부모들의 요구에 엄청나게 시달렸을 것이다. 그러고보면 뜻이 없는 게 아니다. 뜻을 이해하지 못하는 세상이 있을 뿐이다.