-

-
숨마쿰라우데 스타트업 중학수학 2-하 (2025년용) - 2015 개정 교육과정 ㅣ 중등 숨마 수학 (2025년)
이룸E&B 편집부 지음 / 이룸이앤비 / 2019년 3월
평점 :

구판절판


반복 학습으로 자신감을 기르는 유형 학습
숨마쿰라우데
스타트업 중학수학 2-하
안녕하세요 :)
최근에 셋째가 시작한 수학 교재는
<숨마쿰라우데 스타트업 중학수학 2-하>입니다.
셋째는 중2 수학 2학년 1학기 유형 문제집이 끝나가고
심화서로 공부할 계획입니다.
그러면서 중2 2학기 과정도 개념을 조금씩 공부하고 싶어 했어요.
중2 1학기 공부를 하면서 어려운 점이 있었어요.
그래서 유형서로 바로 공부하기보다는
한 개념씩 쉬운 문제로 먼저 공부한 후에
유형서로 들어가고 싶어 했어요.
2학기 수학의 징검다리가 될 교재로
<숨마쿰라우데 스타트업 중학수학 2-하>를
선택한 이유입니다.
<숨마쿰라우데 스타트업 중학수학 2-하>는
한 페이지에 한 개념씩 구성되어 있고
개념 이해를 돕는 유형별 기초 문제를
바로 풀어볼 수 있어서 좋더라고요.
무엇보다 자신감이 떨어져 있는 셋째에게
자신감을 생기게 해서
굿이었어요.
그럼 <숨마쿰라우데 스타트업 중학수학 2-하> 볼게요.

숨마쿰라우데 스타트업 중학수학 2-하는
1272개의 문제를 담고 있어요.
표제에서 느껴지듯 각 학기 첫 교재로 선택하면
좋은 교재랍니다.
한 개념 한 개념씩 공부할 수 있고,
반복해서 공부함으로써 계산 실수를 줄일 수 있어요.


차례입니다.
2학기의 시작은 삼각형의 성질입니다.
이등변삼각형과 직각삼각형,
삼각형의 외심과 내심,
평행사변형과 여러 가지 사각형의 성질을 배워요.
다음은 도형의 닮음과 닮음의 활용을 배워요.
도형의 닮은 조건을 알아보고
평행선과 선분의 길이의 비, 삼각형의 무게중심,
닮음 도형의 넓이와 부피를 공부해요.
그다음 피타고라스 정리를 배웁니다.
사건에 따라 발생할 수 있는 경우의 수,
그리고 확률 계산법을 배웁니다.
50일 완성 학습 PROJECT예요.
핵심 개념 144개를 하루에 30분씩 50일 동안
내 것으로 만들어 볼 수 있게 설계되어 있어요.
공부하는 법도 있네요.

1단원은 삼각형의 성질입니다.
삼각형은 초등시절에도 중1 과정에서도 조금은 배웠어요.
이번에는 이등변삼각형과 직각삼각형을 배웁니다.
삼각형의 외심과 내심도요.
상황에 맞게 스스로 공부 계획을 세울 수도 있어요.
이등변삼각형과 직각삼각형이에요.
개념 설명이 정리되어 있네요.
개념 NOTE에 요약되어 있는 것은
꼭 알아야 할 내용이네요.
정리된 개념을 다시 한 개념씩 풀어 설명해 놓고
개념을 확실하게 이해할 수 있게 쉬운 문제들이 나와 있어요.
이렇게 개념마다 문제를 풀어보면서 개념 이해를 할 수 있으니
셋째가 무척 좋아했어요.
특히 문제가 쉬우니까 생각했던 것보다
쉽다면서 쓱쓱 푸네요.
이등변삼각형의 성질입니다.
이등변삼각형의 두 밑각의 크기는 같아요.
꼭지각의 이등분선은 밑변을 수직 이등분해요.
이등변삼각형의 성질을 이해했다면 문제를 해결해야죠.
마지막 문제는 '학교 시험 맛보기'로 구성되어 있어요.
마지막 문제까지 맞췄고요.
이등변삼각형이 되는 조건이 있어요.
두 내각의 크기가 같은 삼각형은 이등변삼각형이에요.
어떤 삼각형이 이등변삼각형임을 보이려면
두 내각의 크기가 같음을 보이면 됩니다.
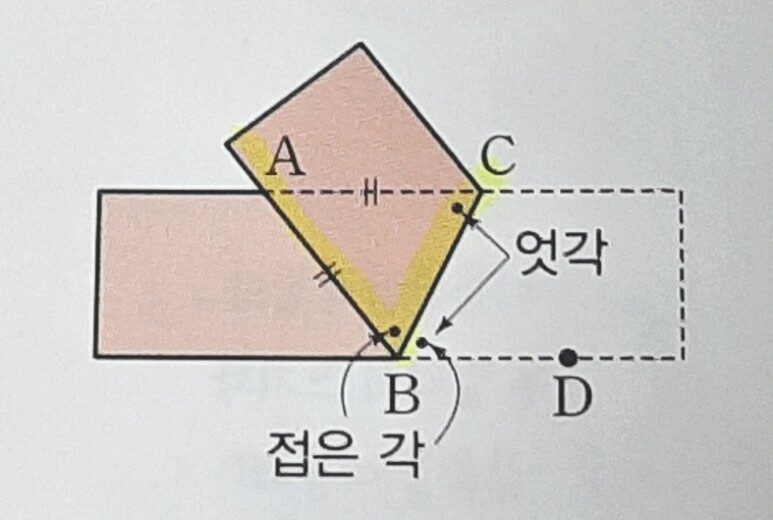
폭이 일정한 종이를 접었을 때 접은 각과 엇각은 서로 같아요.
폭이 일정한 종이를 접었을 때 x의 값과 ∠x의 크기를 구해보았어요.
이등변삼각형의 성질은
삼각형의 세 내각의 크기의 합은 180°이고,
삼각형의 한 외각의 크기는 이와 이웃하는 각을 제외한
나머지 두 내각의 크기의 합과 같아요.
이등변삼각형의 두 밑각의 크기는 서로 같고요.
이 점을 활용하여 각의 크기를 구해 보았어요.
Mini Review Test예요.
앞에서 배운 개념들을 생각하며 풀어보았는데요.
어렵지 않았다고 해요.
소단원이 끝나는 부분에 Review Talk Talk이 있어요.
카톡 느낌으로 중요 개념을 대화 형식으로 알려주네요.
이 내용 중 잘 모르는 개념이 있어서는 안되겠죠?
<숨마쿰라우데 스타트업 중학수학 2-하>
SUB NOTE 정답 및 해설입니다.
정답은 상자에 들어 있어 바로 확인 가능하고
해설도 있어서 혹시 못 풀겠는 문제는
확인하면 될 것 같아요.
★★ 출판사를 통해 교재만을 지원받아 직접 작성하였습니다 ★★