수치해석의 기본 - 이창영

수치해석의 기본
이창영 지음 / 교문사(청문각) / 2008년 10월

정적분에서, 뉴튼의 방법이다, 심프슨의 방법이다 해서 다양한 기법들이 쓰입니다. 그런데 이런 기법들은 엄밀한 공식을 통해, 그야말로 0.00000001의 오차도 없이 값을 구하는 게 아닙니다. 근삿값을 통해, 정답에 가장 근접한 숫자를 얻고 만족하는 거죠.

심프슨의 방법을 예로 들어 보겠습니다. 이 책의 3부 8장에서 다뤄지는데요. 존재하는(혹은 상상 가능한) 함수들 중 상당수는 역도함수를 찾아 적분할 수가 없습니다. "역(逆)도함수"는 예전 중등 교과 과정에서 원함수, 또는 원시함수라 부르던 것의 다른 이름입니다. 물론 미분이 안 되는 것도 꽤 많지만, 적분은 한 걸음 더 나아가, 어찌 보면 "원칙적으로 안 되고 운이 좋아야 가능한 것"으로 보는 게 맞습니다.

삼각함수 중 지극히 예외적인 형태, 무리함수의 대부분 등은 원시함수가 존재하지 않습니다. 예를 들어,

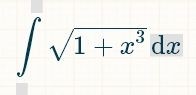
이런 것은 역도함수(antiderivative)를 못 구합니다. 공학용 계산기에 넣고 돌려 봐도 마찬가지입니다. 학부 과정에서 시험에 나오는 문제들은, 아무리 그 겉모습이 복잡해도, 결국엔 답이 나오도록 출제자가 고민해서 짜낸 것들입니다.

안되는가 보다 하고 말 게 아니라, 본래 적분(식, 값)을 구하는 목적은, 함수의 그래프를 그리고 그 곡선 아래 부분의 넓이를 구하는 데에 있습니다(정확하게는, 그 곡선의 아래로부터 내려와서, x축으로 둘러싸인 부분까지의 넓이). 그렇다면, 꿩 잡는 게 매라고, 결과에서 극히 작은 차이만 날 뿐이라면, 근삿값을 구해서 (실제에) 응용하는 것도 나쁘지 않겠고, 오히려 전쟁에서 성문을 정면 돌파할 수 없으면 개구멍이라도 찾아서 돌파하는 요령이 칭찬 받아 마땅한 것(그 정도가 아니라 아예 천재)입니다. 애초에 적분의 목적이 이쪽이므로 머리 좋은 학자들은 근삿값을 정밀히 구하는 기법을 일찍부터 발전시켜 왔습니다. 근삿값이라고 하면 초 5, 중 1 정도에 마지막으로 배우고 이후에는 본격(?) 정밀 수학만 제대로 쳐 주는가 보다 처럼 여길 수 있지만, 전혀 그렇지 않습니다. 이런 근삿값 기법 역시 수학의 한 본령을 이룹니다. (공학 수학에 더 가까운 성격이긴 하지만 당시에는 뚜렷한 분화가 이뤄지지 않았겠죠)

미적분의 기초에서 다항함수(엑스의 제곱, 세제곱, n제곱 등등의 곱과 합으로 표현되는 것들)을 미분, 적분하는 법을 배웠습니다. 이 정도는 고교에서 문과생들도 다 다루는 것입니다(7차만 제외). 방법은 매우 쉬우므로(구구단보다 쉽습니다. 구구단은 72개의 긴 식들을 외우는 과정이라도 거치죠), 누구나 다 조금만 시간을 투자해서 쉽게 갖고 놀 수 있습니다.

생긴 것만 봐도 까다로운 삼각함수, 로그함수 들 중 상당수 불가능한 꼴은, 이 다항함수 중 가장 근사한 식을 찾아서, 그 다함함수의 정적분으로 값을 구해내면 됩니다. 이와 그 취지가 비슷한 것 중에 테일러 급수(전개)라는 것도 있는데, 이 책의 2부 4장에서 다룹니다.