
초등 수학에서 고등
수학까지, 주제별로 접근하는 수학 개념 읽기!
기초 개념에서 출발하여 상위 개념으로 나아가는 새로운
수학 학습법!
수능시험을 앞두고 나는 ‘수포자’라 단언했다. 아무리 많은 시간을 할애해도 수학 성적은 이렇다 할 반전을 보이지 않았고, 결국에
수학은 깔끔하게 포기하는 것으로 마음을 비웠다. 분명 중등 수학을 공부할 때만 하더라도 수학은 재미있는 과목이었고 하는 만큼 성적도 나왔는데
고등학교로 진학하면서 수학은 재미없고 어려운 과목이 되어버렸다. 대체 어디서부터 잘못된 것인지, 그렇게 수학과는 끝내 친해지지 못한 것으로
일단락이 되었는데 최근에 들어서 다시 고민이 되기 시작했다. 아직 5살에 불과하지만 이제 덧셈과 뺄셈에 대한 개념을 익히기 시작한 아이에게 이
단계를 넘어서면 그땐 어떤 방법으로, 효율적으로 가르칠 수 있을 것인지 막막해진 것이다. 당장 수학문제집이라도 찾아서 풀어볼 수도 없는 노릇이고
무엇부터 시작하면 좋을지 고민하던 찰나에 창비 출판사에서 <수학 교과서 개념 읽기>라는 책이 나와서 관심이 갔다. 수와 연산 세트,
도형 세트까지 출간되었는데, 이 중 가장 기본이라 할 수 있는 수와 연산부터 시작해볼까 한다.
자연수부터 허수까지,
덧셈에서 로그까지
우리나라 교육 과정에 따르면 초등학교, 중학교, 고등학교 12년에 걸쳐 수학 개념, 원리, 공식 들을 배운다. 수학 교과서 한 단원의
내용을 제대로 이해하기 위해서는 이전 학년에서 배웠던 연관된 개념과 원리를 모두 알고 있어야 한다. 그런데 몇 년 전에 배웠던 수학 지식을 모두
기억해서 활용하고, 지식 사이의 관계까지 파악하는 것은 쉬운 일이 아니다. 예를 들어 고등학교 수학에서 배우는 허수를 이해하기 위해서는
초등학교에서 배운 양의 정수와 0, 중학교에서 배운 음의 정수와 유리수, 무리수의 개념과 이러한 수 사이의 관계를 알아야 하는데, 이를 모두
기억했다가 고등학교 수학 시간에 활용하기가 쉽지 않은 것이다. 게다가 수학과 관련된 많은 책이 수학 개념을 학년별로 구분지어서 설명하는 까닭에
이들 개념 사이의 연관성을 이해하기가 어렵다. 그런 의미에서 <수학 교과서 개념 읽기> 시리즈의 저자는 ‘수학 개념은 서로 이어져
있다’는 점을 강조하며, 초·중·고 수학 교과서에서 흩어져 있는 수학 개념들을 주제별로 모아 한눈에 살펴볼 수 있도록 엮었다. 이를 통해 수학
지식들이 어떻게 연결되어 있는지 보여주고, 수학의 개념과 원리, 공식 사이의 관계를 이해하게 하는 데 도움을 주고자 한다.
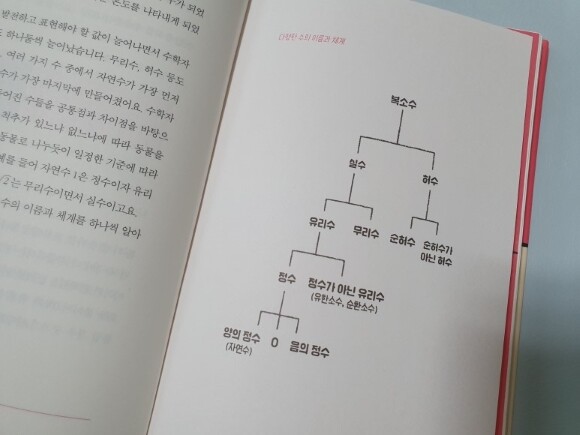
‘수’ 편에서는 초등학교에서 배우는 자연수와 0부터 고등학교에서 배우는 허수와 복소수까지, 학교에서 배우는 모든 수를 담고 있다.
자연수와 분수처럼 원시 시대부터 일상생활에 사용되었던 수를 이해하는 것에서 출발해 무리수, 계산을 획기적으로 편리하게 만들어 준 소수,
수학자들이 상상을 통해 만들어 낸 허수 등을 살펴본다. 가장 기본이라 할 수 있는 자연수에서부터 새로운 수가 만들어지게 된 과정과 어원을
차근차근 살펴보다보면 수의 체계를 한눈에 파악할 수 있다.
소수점 아래 숫자가 반복되는 부분이 있는 소수를 순환소수라고 해요. ‘순환’은 매일 같은 구간을 도는
순환 버스같이 일정하게 반복하는 것을 뜻하는 단어예요. 순환소수에서 반복되는 부분을 순환마디라고 합니다.
그런데 반복되는 숫자는 대체 몇 번이나 써야 할까요? 0.333…에서 3을 몇 번이나 써야 보는 사람이
3이 순환마디구나, 하고 알 수 있을지 아리송합니다. 이와 같은 불편을 없애기 위해 우리나라에서는 순환마디 위에 점을 찍어 나타내기로 했어요.
순환마디의 숫자가 하나인 경우에는 그 숫자 위에, 순환마디 숫자가 2개 이상인 경우에는 순환마디의 첫 번째 숫자와 마지막 숫자 위에 점을 찍어
순환마디를 나타냅니다. / ‘수 편’ 중에서 83p


<수학 교과서 개념 읽기>의 수 편을 읽으며 참 유익하다 싶었던 것은 초등학교부터 고등학교에 이르기까지 학교에서 배우는
모든 수를 담고 있음에도 불구하고 방대하지 않아 가장 핵심이 되는 내용만 익힐 수 있다는 점이다. 그러면서도 빈약하지 않고 필수 예제를 쏙쏙
담아 초등학생들도 이해하기 쉽도록 설명해놓은 것이 장점이라 할 수 있다.


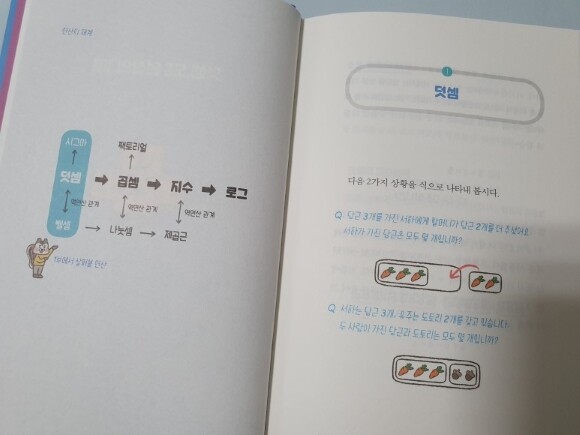
이어 ‘연산’ 편에서는 초등학교에서 배우는 덧셈과 뺄셈부터 고등학교에서 배우는 지수와 로그까지, 학교에서 배우는 모든 연산을 담고
있다. 수학자들이 어떤 불편을 해결하기 위해 덧셈을 곱셈으로, 곱셈을 지수로, 지수를 로그로 바꾸어 계산하게 되었는지 살펴본다. 이 새로운
연산이 만들어지게 된 과정을 차근차근 따라가다 보면 학교에서 배우는 여러 연산들이 서로 밀접하게 연결되어 있으며, 각자의 단점을 보완하기 위해
발전된 것임을 파악할 수 있다. 그도 그럴 것이 ‘연산의 체계’의 그림을 보면 각각의 연산이 어떻게 연결되었는지 자연스럽게 익힐 수 있다. 그간
정밀하게 연결된 연산의 체계를 잘 모른 채 서로 다른 개념이라고 생각하거나 공식만 달달 외웠으니 수학이 어려울 수밖에 없었던 게 아닌가 새삼
깨닫게 된다.
2개 이상의 수나 식을 더하는 계산을 덧셈이라고 합니다. 덧셉이라니, 이미 잘 알고 있는 내용이라
시시하다고요? 그렇지만 덧셈을 빼고 다른 연산을 이야기할 수는 없습니다. 덧셈은 새로운 연산 기호를 약속하는 데 많은 영향을 주었습니다. 예를
들어, 덧셈 기호의 불편한 점을 개선하기 위해 곱셈 기호가 만들어졌고, 이어서 지수, 로그도 생겨났습니다. 또 덧셈을 잘 알고 있으면 뺄셈,
나눗셈, 루트도 쉽게 이해할 수 있습니다. 덧셈을 거꾸로 하는 연산이 뺄셈은 나눗셈과 루트를 약속하는 데 토대를 제공합니다. / ‘연산 편’
중에서 21p



<수학 교과서 개념 읽기> ‘수, 연산’ 편을 읽으며 수학 실력에 상관없이 누구나 쉽게 수학 개념을 정립하는 데 도움이
되는 책이라 만족스러웠다. 특히 나와 같은 부모들이 자녀들의 수학책을 들여다보기 전에 꼭 읽어보기 좋고, 아이가 초등학교 고학년쯤 되면 꼭
읽혀보게 하고 진학시키기를 권하고 싶다. 허수라던지 로그까지는 아이가 이해하기 어려울 수 있지만 내가 배운 덧셈과 뺄셈이, 곱셈과 나눗셈이
어디로까지 나아가는지 그 과정을 지켜보는 것만으로도 좋은 학습이 되리라 생각하기 때문이다. 게다가 공부하는 기분이 아니라 수학의 역사까지 가볍게
살펴봄으로써 편안하게 읽는 재미까지 더하니, 가벼운 마음으로 이 책에 접근하시라 주변에 추천해야겠다.
