천재들이 만든 수학퍼즐32 파스칼이 만든 경우의 수

천재들이 만든 수학퍼즐 32 - 본편, 파스칼이 만든 경우의 수 ㅣ 천재들이 만든 수학퍼즐 32
이운영 지음 / 자음과모음 / 2009년 10월

자음과 모음책들의 묘미는 모든 과정이 몇 교시로 나뉘어져 있어서 책속의 선생님께 과외를 받는 기분이예요. 그래서 혼자서 책을 보더라도 이해하기가 쉽다는 거지요. 책의 내용에 대한 역사부터 천천히 심화까지 일러주시니 더더욱 재미나게 읽어내려 갑니다. 사실 조금 어려운 부분도 있지만 아이들 학년에 맞추어 읽는다면 쉽게 접하게 되더라구요. 울아이들을 보니 그러했어요. ㅎㅎ

천재들이 만든 수학퍼즐 32 파스칼이 만든 경우의 수입니다.

수학퍼즐은 수학퍼즐 익히기와 한세트라 유용하게 활용되지요.

경우의 수는 수학부분에서도 정말 배워두면 생활에서도 유용하게 활용할수 있는 부분입니다.

둘째가 6학년인데 이제 2학기부터 배우게 될 경우의 수네요. 아이들이 경우의 수를 비롯해서 확률을 어려워 하더라구요. 쉬운듯 하면서 어려운 경우의 수 이제 만나볼까요?

경우의 수는 왜 배우는지, 어떻게 구하는지, 합의 법칙과 곱의 법칙은 서로 다르다는거...이러한 순서데로 9교시까지 나열되어 있네요.

경우의 수를 아는 사람은 주어진 일에 대한 모든 경우를 예측할수 있어요. 앞으로 일어날 모든 경우에 대비 할수 있다는 이야기지요.

아이들 교과서에 기본적으로 나오는 문제지요. 동전과 주사위, 가위바위보 문제가 가장 많이 나오는걸로 알고 있어요. 나올수 있는 경우를 순서쌍이나 수형도를 그려서 나타내다 보면 쉽게 경우의 수를 알수 있어요.

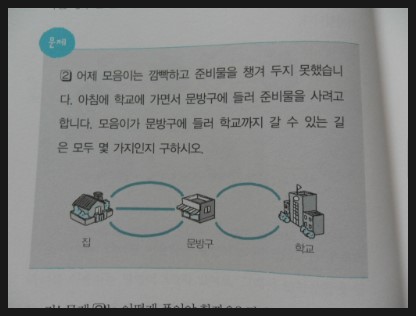
다음으로 많이 나오는 문제가 바로 이러한 문제일 겁니다. 경우의 수 뿐만 아니라 거리를 구하는 문제로도 많이 나오지요.

여기서 주의할점은 두 사건이 동시에 일어날때를 주의해야해요.

곱의 법칙을 활용해서 A와 B 두 사건이 동시에 일어나는 경우의 수 m * n가지

(사건 A가 일어나는 경우의 수 : m, 사건 B가 일어나는 경우의 수 : n)

이렇게 경우의 수는 합의 법칙과 곱의 법칙만 잘 활용하면 실수하지 않을 거예요.

문제는 중학교때 배우는 확률입니다.

중2인 아들이 2학기 1단원으로도 배우게 되는 확률. 걱정부터 앞서네요.

그러한 아들에게 권하고 싶네요. 미리 책에서도 나오듯 순열을 먼저 익혀 두라고... 

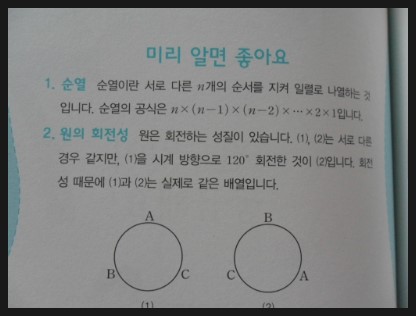
고등학교 수학에도 연계되는 확률을 잘 배워둬야 할것 같네요. 앞의 경우의 수보다 순열을 먼저 보니 왠지 더 쉽게 느껴져요. 저야 이미 한번은 배운 부분이니 그러겠지만 처음만나는 울아들이나 딸은 어렵게 생각되나 봅니다. 그래도 이책이 울아들, 딸 2학기 과정과 연계된다 생각되니 더 세심하게 보게 해야겠네요.

아이가 우리집처럼 초6학년과 중2라면 정말 권하고 싶어요. 이번 여름방학에 만난 '파스칼이 만든 경우의 수' 덕분에 울아이들 2학기 수학 문제 없겠죠? ㅎㅎㅎ