유클리드의 마지막 강의를 듣는것 같다. 원래는 61권인 공간도형 하기전에 읽었어야 하는데 순서가 바뀐것 같다. ㅎㅎㅎ 웬지 유클리드와 친해진 느낌은 뭐지?
신선같은 하얀 수염을 길게 드리운 모습이 친숙한 할아버지를 만난듯 기쁘다.
이번책 원론엔 그동안 궁금했던 모든 도형의 기초를 배우는것 같아 더 쉽게 접한것 같다.
교과 연계를 보아도 초3학년부터 고등학교까지 이어진다.
유클리드의 대표적인 책이라해도 과언이 아니다. 유클리드의 원론을 보면 기하학을 중심으로 수에 대하여 설명되어지고 있다. 그러한 원론이 23권으로 이루어져 있다니 과히 놀랍다. 새삼 수학자들의 머리는 어느정도일까 궁금하기까지 하다.
먼저 원론을 읽고 이해한 다음 다른 도형들로 넘어가면 좋을듯 싶다. 책의 앞쪽만 본다면 다른책들과 겹치는 부분도 있다. 그러나 수학공부는 반복이란점을 감안하면 해도 해도 끝이 없다는 것만 남는다. 그러니 읽은 부분이라도 또 읽어보시길...
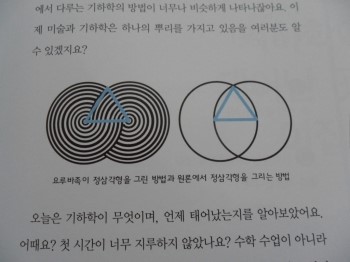
첫번째 수업으로 기하학에 대해 나온다. '셀수 있는 수', '얼마'를 나타내는 기. '왜'를 나타내는 하. 학문을 나타내는 학. 이러한 의미의 기하학이다.
기하학이 처음 생겨난 곳이 이집트란다. 그러한 것을 보면 이집트인들로 인해 수학이 발전한것 같다. 파라오의 무덤을 만들면서 거대한 규모와 건축술이 발전하게 되었다고 한다.
이러한 공식도 모두 이집트인들의 생각에서 나왔다니 다시한번 놀랍다.
그때나 지금이나 자신의 주장들이 맞다고 우기는 것은 여전한가 보다. ㅎㅎㅎ
역시나 요 원론에서도 내가 어려워 하던 부분인 유추와 추론에 대해 나온다.
저번 공간도형에서도 말했듯 증명을 나타내는 일은 나에겐 어렵다. 아들도 어렵다고 한다. 이러한 것도 유전인가? 안되는데....ㅎㅎㅎ
귀납적 추론과 연역적 추론 구분법을 잘 알고 증명을 잘 해야겠다. 수학에서 가장 강력한 증명 방법은 연역적 추론이라니 핵심을 배운 느낌이다.
유클리드의 기하학과 리만의 비유클리드 기하학과 데카르트의 공간을 잘 이해한다면 도형부분에서는 별 어려움은 없으리라 본다. 그 세인물 덕분에 우리는 어려운 수학을 배우게 되었다. 왜 이렇게 어려운 수학을 배워서 어디다 써먹을까? 하고 의문이 생겼는데 울아이들도 똑같은 질문을 한다.
이책에서도 씌여있다. 그러한 아이들에게 권장해 보라고....
글밥과 글씨의 크기가 적당해서인지 별 어려움 없이 읽어내려가는 울아이들. 아마 모두 이해했다면 거짓일 것이고 차차 거부감없이 읽어내려간다는 것만으로도 만족한다.
이제 중1인 울아들이 어려워했던 도형부분은 끝이났다. 제발 이번 기말고사에 만족할만한 점수를 기대하면서 다음은 어느 인물을 탐구할지 고민좀 해봐야겠다.