공간 추리 퍼즐 2

공간 추리 퍼즐 2 - 논리적 사고 센스를 키우는 뇌풀기 퍼즐 100 ㅣ 공간 추리 퍼즐 Logical Puzzle Series 2
무라카미 료이치 지음, 장은정 옮김, 이나바 나오키 퍼즐 문제 구성 / 그린페이퍼 / 2017년 3월

이 책은 첫째 스도쿠 즐겨 푸시는 어르신들, 둘째 수학에 벌써부터 공포감을 느끼며 질려하는 초등학생들이 읽으면 유용할 것 같습니다.

스도쿠는 물론 치매 예방과 두뇌활성화를 위해 좋은 오락거리지만, 너무 같은 종류, 방향의 훈련에만 치우치면 애써 들인 시간이나 노력만큼의 성과가 안 나올 수 있습니다. 그 역시 정해진 루틴이 되어 두뇌가 그쪽으로만 길이 들어 버리면 두뇌를 훈련시키는 보람이 없죠. 스도쿠보다 훨씬 난도가 높은 바둑을 즐겨 두시는 분들도 치매에 걸리는 예를 보면 알 수 있습니다. 그래서, 머리에 자극을 주려면 평소에 안 해 버릇하던 트레이닝 수단을 택해야 합니다. 또한 이런 이치는 어르신들뿐 아니라 어느 연령대라도 마찬가지로 적용되겠습니다.

초등학생들에게는... 만약 공부를 꽤 잘하는 유형이라면 이 책에 실린 문제는 간단한 일원, 혹은 이원일차 방정식을 통해 쉽게 풀 수 있을 겁니다. 그런 아이들에게는 이 책에 제시된 풀이(또, 학교에서 가르치는 표준적인 방법) 말고, 다른 방법을 혹시 생각해낼 수 있을지, 도형을 다른 각도로 파악할 수는 없을지, 한번 과제를 던져 보는 것도 좋을 것 같습니다. 그렇지 않고 현재 학교 과정을 따라가기 버거워하는 애들이라면, 이처럼 쉽고 간단한 문제 풀이를 통해 도형이 그리 어려운 과제가 아님을 알고 자신감을 심어 줄 수도 있겠습니다.

난이도는 모두 5단계입니다. 1단계는 정사면체, 5단계는 정이십면체 심벌로 각각의 문제에 표시되었는데, 정다면체가 모두 4, 6, 8, 12, 20면체 다섯 종류가 있음을 상징합니다. 아이들에게라면 왜 정다면체(볼록)는 저 다섯 종류밖에 없는지 한번 생각해 보게 하는 것도 좋겠습니다.

책 제목은 "공간"이지만, 입체공간이 아닌 평면공간 도형 문제만 나옵니다.

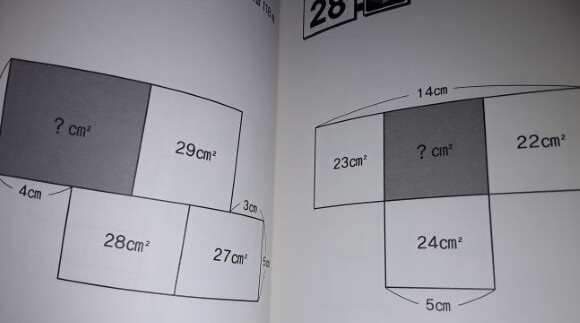
왼쪽 그림을 보시면 아래 줄 두 직사각형을 하나로 묶어 보는 게 포인트입니다. 묶어서 새로 생긴 직사각형의 넓이는 55㎠인데, 이제 55÷5=11를 하면 가로줄의 길이가 바로 나오죠. 이게 책 해답에 제시된 방법인데,

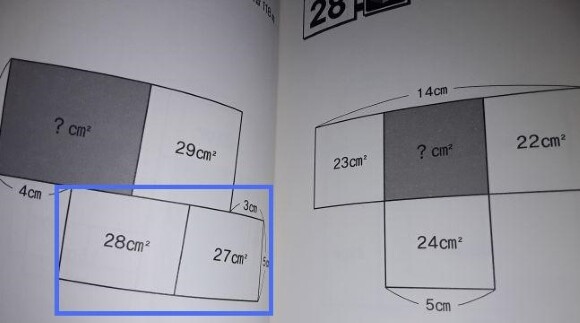
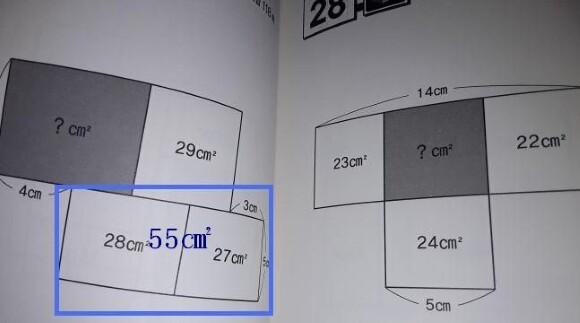
저는 다른 방법으로 풀어 봤습니다.

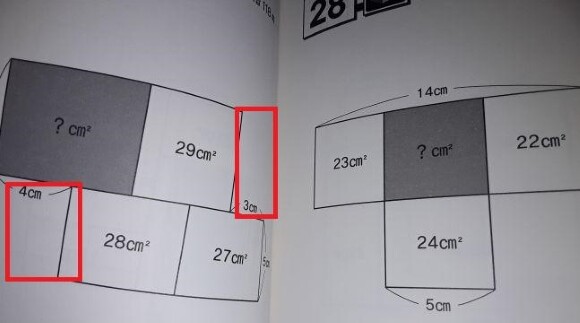
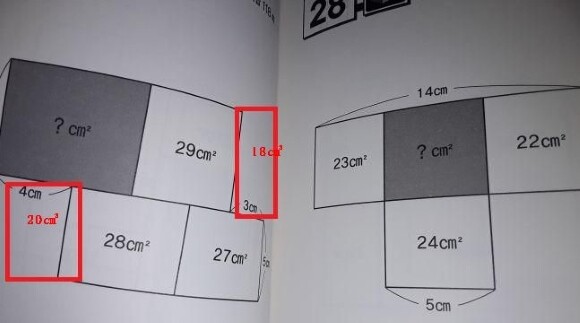
20+28+27 = 75 입니다.

한편, 윗 줄은 ? + 29 +18 = ?+ 47 이죠.

그런데 윗 칸의 세로 줄이 6cm, 아래 칸이 5cm이므로 널이의 비도 6:5가 되어야 합니다.

?+47 : 75 = 6 : 5 이므로, ?+47 = 90 이라야 합니다.

그러므로 ?는 43㎠ 이 됩니다.

이상이, 이 책에 나온 해답 말고 제가 생각해 본 풀이입니다. 

어떠신지요? 이처럼 모든 문제는 다른 시각으로 보면 다른 해법이 반드시 드러나게 되어 있습니다.

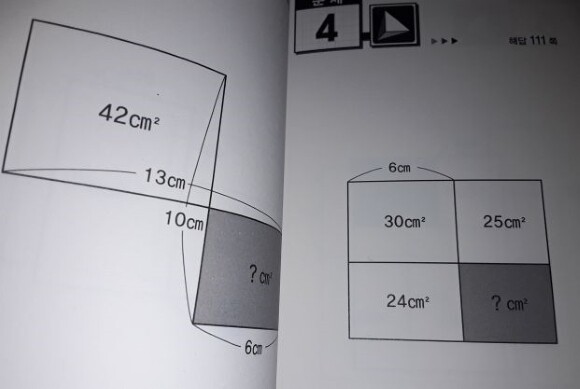
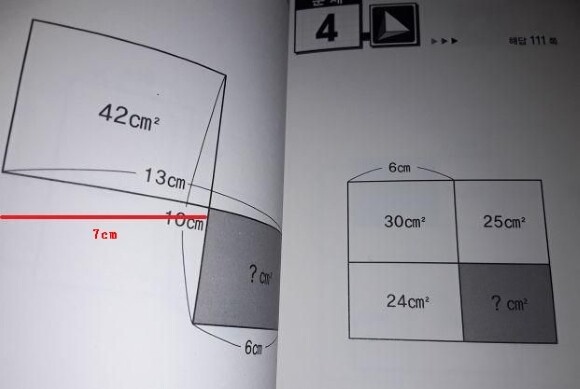
그러므로 위 직사각형의 세로 길이가 6cm라는 건 바로 알 수 있습니다.

이런 저난도 문제는 만약 독자가 초등학생이라면 반드시 혼자 힘으로 풀게 해서 자신감을 심어 줘야겠죠.

이제 오른쪽 문제를 보십시오. 푸는 방법은 사실 한눈에 보입니다.

그런데 좀 다른 관점에서 볼 수도 있습니다.

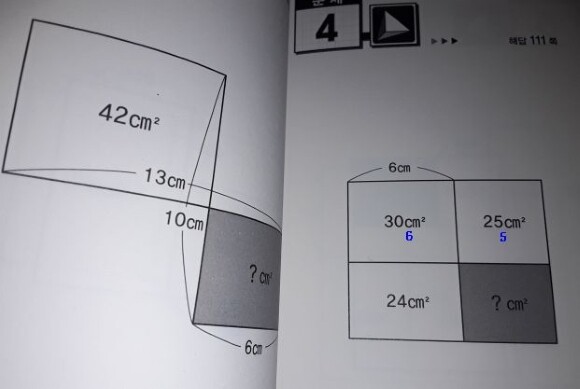
저렇게 직사각형꼴로 나란히 세로, 가로 줄을 공유하는 모습이라면, 넓이와 길이가 같은 비로 이뤄집니다.

넓이가 30: 25면 이 경우는 세로를 공유하므로 가로도 당연히 30:25, 즉 6:5 가 됩니다.

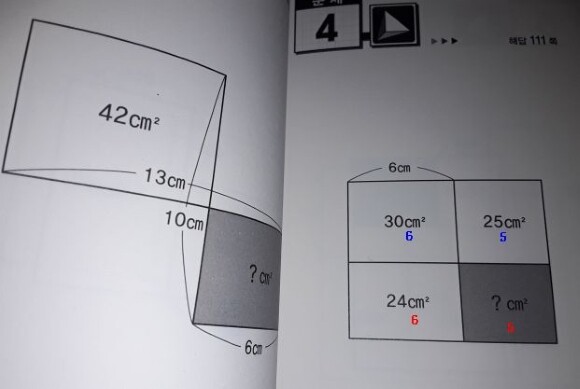
그렇다면 아래 줄도, 24: ? = 6:5 가 되죠. 당연히 ?은 20㎠가 나옵니다.

이처럼 이 책에 나온 상당수의 문제는, 가로와 세로 중 어느 하나를 공유하는 직사각형 쌍은, 넓이의 비가 세로(혹은 가로)의 비와 같다는 점만 알면, 일일이 더하기 빼기를 안 해도 바로 구할 수 있습니다.

다만, 치매 예방용 두뇌 훈련이라면 책에 나온 대로의 풀이가 더 바람직할 것 같기도 합니다. 덧셈 뺄셈을 번갈아 가며 하는 연산 훈련이 이런 용도로는 더 효율적일 수도 있으니 말입니다.