우주와 교감하는 장

마틴 가드너 수학자의 노트 - 수리 논술, 대수·조합·논리·기하
마틴 가드너 지음, 아이작 아시모프 서문, 윤금현 옮김 / 보누스 / 2013년 4월

이 책은 아니고 다른 책에서 읽은 말이지만, 우주의 생성과 작동 원리를 이해하려면 반드시 수학을 알아야만 가능하다고 합니다. 이 마틴 가드너의 책에는 그 소갯말로 이런 멋진 표현이 있더라구요.

"마틴 가드너의 책은 수많은 천진한 어린이들을 수학의 세계로 이끌었고, 수많은 수학 교수들을 천진난만한 어린이로 만들었다."

큰 관점에서 보면, 수학 역시 거대한 놀이임에 틀림 없는 것 같습니다. 레고도, 지능이 뛰어난 아기가 아무래도 활용도를 높여서 잘 가지고 놀듯, 수학 역시 그걸 갖고 노는 사람의 지적 수준에 따라 편차가 있을 뿐, 기본적으로 실용의 영역과는 관계 없는 차원에서 효용을 발휘하기 시작한 거니까요. 물론 이 책에도 나와 있듯이, 아르키메데스 같은 이는 볼록 거울을 이용해서 적인 로마군을 퇴치하는 전쟁의 기술로 수학을 응용하기도 했습니다만, 그거야 천재의 아주 예외적인 경우겠죠.

이 책에 보면, 고서점에서 옛 잡지(<어메이징 스토리>라는 제호인데, 물론 가상의 잡지일 것입니다)를 사려는 어느 신사의 이야기가 나옵니다(16장, pp199-122). 서점 주인의 흥정은 이랬다고 합니다. "가장 최신호는 1달러, 그 다음으로 최근 것은 3달러, 이런 식으로 2달러씩 늘려 가면...." 이 책을 읽으신 분들은, 이 장에서 무엇을 느끼셨습니까? 문제를 푸는 결정적 힌트는, "한 책에만 당신(와이프) 나이의 5배를 지불했어."라는 주인공의 대사입니다. 얼핏 들어 별 말이 아닌 것 같지만, 대단한 힌트가 숨어 있습니다. 그 말은, 두 그룹으로 나뉜 책들 중에, 그 가격에 해당하는 책은 어느 한 그룹에만 들어 있다는 뜻이잖아요? 각 그룹은 최대한 같은 권수를 가져야 하므로, 만약 총 구입 권수가 짝수라면, 이 가격은 이 그룹이나 저 그룹 모두에 포함되어 있을 수도 있습니다. 그런데 주인공은, "단 한 권'이라고 못을 박고 있습니다. 그렇다면, 총 구입 권수는 홀수라는 말이죠. 이를 결정적 힌트로 해서 이 퍼즐은 풀려 나가게 됩니다. 또, 서점 주인 노인은 왜 두번째 제안을 하면서 그리 큰 인심이나 쓰는 투로 말을 했을까요? 만약 첫번째 제안대로라면, 등차수열의 합은 책이 n권일 경우, n의 제곱이 됩니다(이 책 p122 위에서 셋째 줄). 그러나 두번째 제안대로라면(책에는 좀 시원한 설명이 안 나와 있습니다만), 다음과 같은 일반식이 나옵니다.

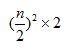
그래서, 첫째 제안보다 절반으로 가격이 내려가는 결과입니다. 이 정도면 매도자가 스스로 가격을 반으로 후려 치는 거니 인심을 쓰는 척도 할 만하죠. 다만 마지막에 단서로 단, "100의 배수는 되어야 해." 가 함정이지만요.

그런데, 과연 이런 시시한 문제를, 대학을 졸업하고 사회에 이미 편입된 어른이 어디 가서 진지한 화제로 내세울 수 있을까요? 말 한 번 잘못 꺼냈다간, 영 모자란 사람 취급 당하기나 쉽습니다.

제가 앞에서 인용한 소갯말의 그 표현은, 그런 의미에서 중요한 함의를 지닙니다. "수학은 원칙적으로 어린이의 천진한 마음으로라야 그 진정한 접근이 가능한 놀이이다."

다 시 토픽으로 돌아가서요, 이 16장에서 다루는 문제라면 우리 한국에서는, 보통 청소년기에 학교에서 배우는 등차수열과 같습니다. 가상의 주인공은 "그만한 돈이 없습니다."라고 하지만, 사실 등차수열의 합은 그렇게 감당 못할 정도로 늘어나지는 않습니다. 무서운 건 등비수열이죠. 이 책 21장(p153)이 다루는 토픽이 바로 그 등비수열입니다.

21장의 화제는 참으로 흥미롭습니다. 읽어보신 분들은 다 알겠지만, 바이러스라는 게 알고 보면 정보의 배열에 불과하다는 일본 과학자들의 가설을 퍼즐화하여 소개하고 있네요. 그 가설은 별 신빙성이 없는 것으로 판명났지만, 중요한 사실을 놓치면 안 되겠죠. 왜 외계인들이, 번거롭게도 (우리 지구인이 하는 방식처럼) 전산 부호의 전송이 아닌, 바이러스의 형태로 정보의 매개체를 삼았을까요? 그 이유는 생명체(바이러스를 생명으로 본다면)의 무서운 증식 속도 때문에 그렇습니다. 어떤 단계에서 아무리 적은 레벨에 머무르는 숫자라도, 매 단계를 거칠 때마다 일정 배수가 곱해짐이 보장되기만 한다면, 그 수는 어느 순간에는 감당 못 할 만큼 거대한 수치가 된다는 건 고등학교 수준의 등비수열 원리만 배워도 알 수 있습니다. 이 장은 이 당연한 사실을 잘 응용해서, 흥미로운 문제로 가공하고 있습니다.

마틴 가드너의 이름에 확 끌려서 이 책의 구입을 고민하는 분이라면, 아마 그 생각이 들 겁니다. "과거에 사계절 출판사에서 출간되었던(지금도 시중에서 팔고 있습니다) 그 두 권과 혹시 내용이 겹치는 건 아닌가?" 조금 실망스러운 건, 그런 부분이 꽤 있다는 거고, 그것도 책의 첫 장 첫 토픽이 바로 예전 그 책들에서 본 문제라는 거죠. 그런데, 총 33개 장 중 그 두 권의 내용과 겹치는 건 11개 정도고, 그 내용도 완전히 동일하지는 않습니다. 그 책들은 일반 원리의 설명이 많았다면(그리고 매혹적인 일러스트가 있었죠), 이 책은 보다 문제 위주로 편집되어 있습니다. 그 책들의 분위기가 좀 더 유럽적이었다면, 이 책은 유머 코드까지 포함해서 다분히 미국적입니다. 무엇보다, 비교적 최근의 성과를 반영한 원리와 주제가 많이 반영되어, 읽는 이의 입장에서는 <그 책들>의 속편으로 받아들일 수도 있습니다. 몇 군데 깔끔하지 못한 번역이 흠이지만, 옛 추억을 다시 떠올리고 싶은 어른들에게 아주 제격이라 말씀 드리고 싶습니다. 같이 한번 <레고>를 갖고 놀아 보자구요!