처음 읽는 수학의 세계사, 우에가키 와타루

처음 읽는 수학의 세계사 - 인류와 함께 한 수학의 역사
우에가키 와타루 지음, 오정화 옮김 / 탐나는책 / 2023년 2월

고대 수학부터 미분적분까지 수학의 발전을 꼼꼼하게

구체적으로 서술한 수학사의 결정판 !

이집트나 바빌로니아에서는 덧셈과 뺄셈은 간단하게

계산했지만, 곱셈과 나눗셈은 여러 가지 다양하게 궁리하며

계산했다. 고대 이집트의 곱셈은 '2배법'이라고 부를 수 있다.

가정법이란, 먼저 답의 수치를 가정하고, 그 가정한 수치를

사용해 문제가 가리키는 대로 계산하여 하나의 값을 도출한다.

그리고 그렇게 얻은 수치와 처음에 주어진 수치를 비교하는 것이다.

고대 오리엔트의 수학은 구체적이고 개별적이며, 실용적인

여러 문제에 대한 풀이집이라는 점이 특징이다.

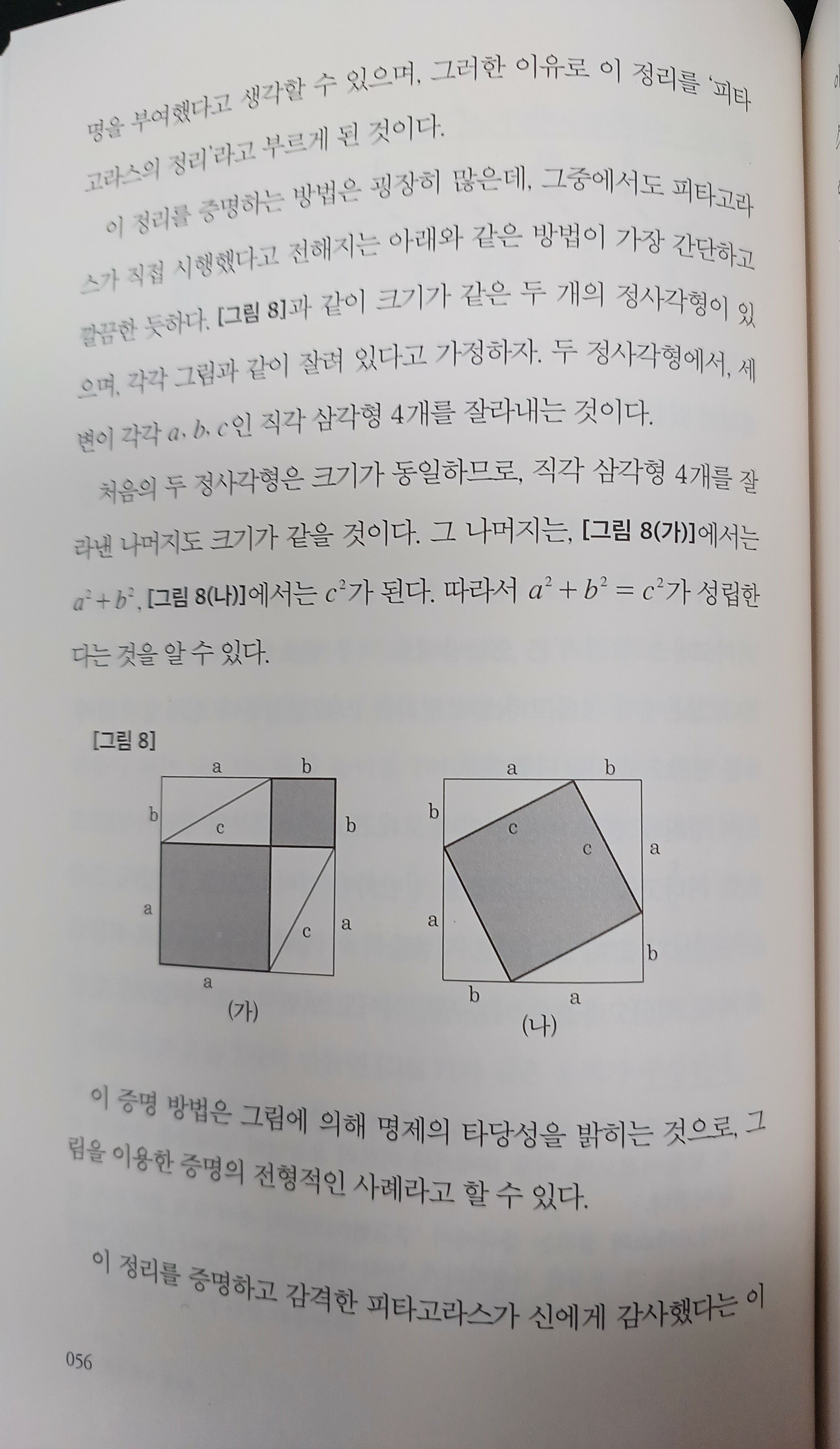
두 정사각형에서, 세변이 각각 직각 삼각형 4개를 잘라내는 것이다.

처음의 두 정사각형의 크기가 동일하므로, 직각 삼각형 4개를

잘라낸 나머지도 같을 것이다. 이 증명 방법은 그림에 의해

명제의 타탕성을 밝히는 것으로, 그림을 이용한 증명의 전형적인

사례라고 할 수 있다.

 a²+b²=c²

<피타고라스의 정리>

고대 그리스 수학에 현저하게 볼 수 있는 사상은 '피타고라스 → 

플라톤 → 유클리드'라는 계보에 의해 형성되었다고 할 수 있다. 

이러한 사상은 오늘날 '플라톤주의'라고 부른다.

정다면체란 한 종류의 정다각형으로 만들어지고, 각 꼭짓점 주변이

모두 같은 상태가 되는 블록다면체를 말한다.

인도의 십진 기수법에서 0 기호는, 이른바 '기록 숫자'가 아닌

'계산 숫자'의 성격이 부여되면서 '숫자로서의 0'이 확립되었다고

말할수 있다. 다시 말해 인도에서 0이 발견된 것은, 빈자리를 

표시하는 기호가 있었으며, 십진법 자릿수 표기에 의해 필산이

이루어졌다는 두 가지 요인이 있었다고 할 수 있다.

오늘날 아라비아 수학 혹은 산용 수학이라고 불리는 수학을 

사용하는 필산은 인도에서 아라비아로 전해진 것이다.

수판셈의 보급은 명나라 시대의 가장 큰 특징이라고 할 수 있으며,

<산법통종>을 비롯해 명나라 시대 대부분의 주산서가 일본으로

유입되었으며, 겐키·덴쇼 시대에는 주판이 일본에 유래되었다고

전해진다.

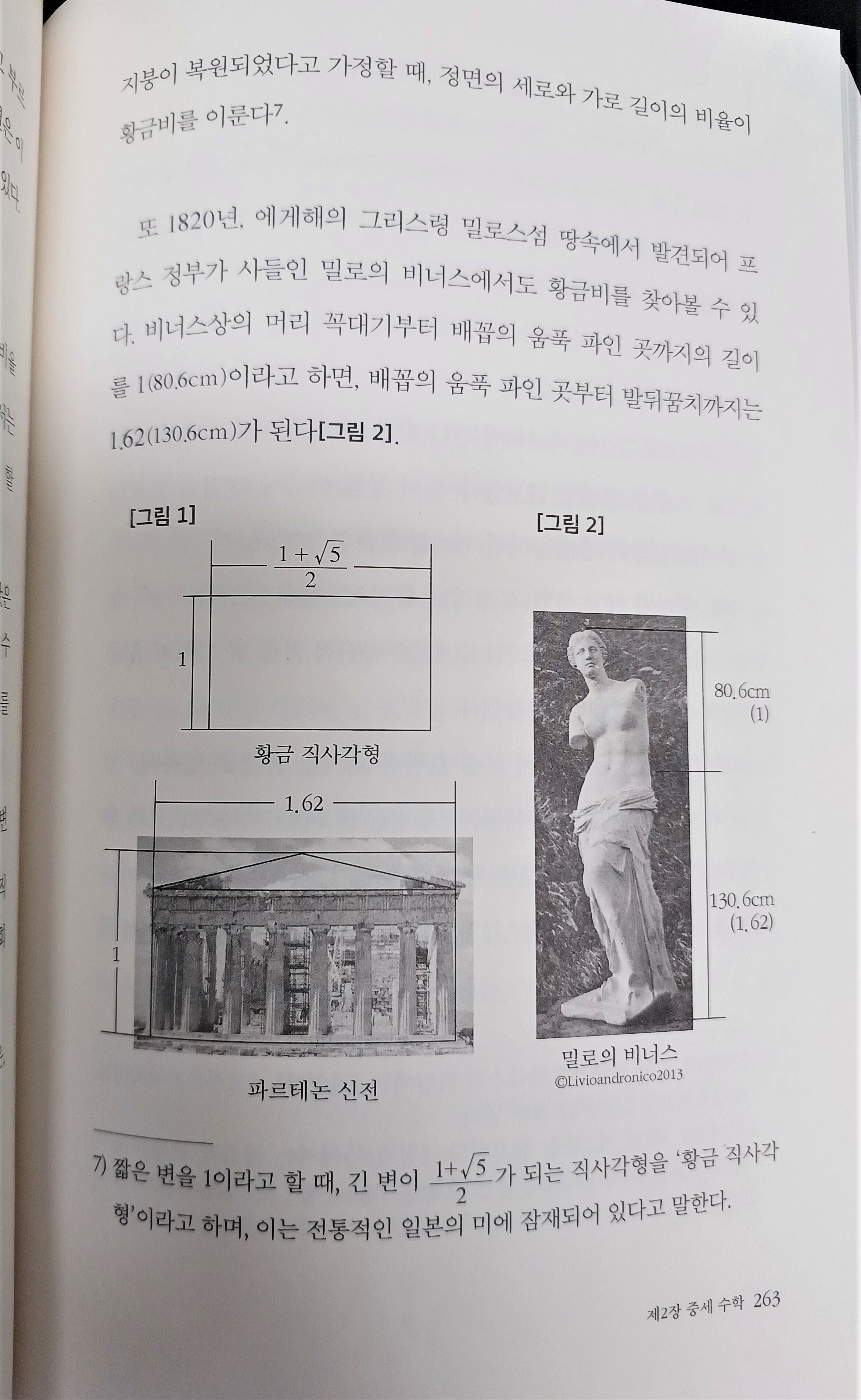
비너스에서도 황금비를 찾아볼 수 있다. 비너스상의 머리 꼭대기

부터 배꼽의 움푹파인곳까지의 길이를 1이라고 하면, 움푹 파인

곳부터 발뒤꿈치까지는 1.62가 된다.

모멘트란 운동 물체의 무게만으로 발생하는 것이 아니라, 아래를

향해 나아가는 경향을 나타내는 성질이며, 무게를 가진 여러 종류의

물체들 사이의 위치 관계에 의존한다.

오늘날 미적분법은 뉴턴과 라이프니츠, 두 사람이 각각 독립적으로

발견했다고 여겨진다. 그러나 두 사람의 접근 방법이 각각 다르다.

뉴턴이 운동학적 고찰에서 출발하여 발견에 이른 데 비해, 라이프니츠는

일반 보편학 혹은 보편적 기호법 확립을 목표로, 그 발견에 도달한 것이다.

@books._day

#처음읽는수학의세계사 #우에가키와타루

#탐나는책 #수학의세계사 #수학 #book #책리뷰 #책추천

#도서추천 #책선물 #좋은글귀 #좋은글 #북스타그램

#글스타그램 #책스타그램 #책추천 #인문학 #역사 #세계사

#2배법 #가정법 #피타고라스정리 #플라톤주의

#황금비 #모멘트 #수학 #세계사 #수학사

#책 #도서 #독서 #철부지아빠