칸토어가 들려주는 집합이야기

칸토어가 들려주는 집합 이야기 ㅣ 수학자가 들려주는 수학 이야기 2
나숙자 지음 / 자음과모음 / 2007년 11월

현대 모든 수학은 '집합에서 시작해 집합으로 흘러 들어간다'고 해도 과언이 아니란다.

그만큼 그 중요성을 콕 집어 주는 말이다.

집합의 개념을 지나 부분집합, 교집합이 나오니 또 마구 복잡해지기 시작한다.

목차를 지나서 좀 차근히 살펴보니 만화와 시로 구성된 '수업 엿보기'를 통해 흐름을 알 수 있다.

또한 원리와 개념 위주의 설명으로 쉽게 이해할 수 있다.

'칸토어와 아이들의 신나는 수학 체험'과 '수업정리' 코너는 주변의 이야기로 이루어져

흥미롭고 수학 용어에 대한 개념을 확실하게 알아갈 수 있다.

우선 칸토어에 대해 간략히 소개하는 부분이 나온다.

그는 1874년 '집합론'을 발표했으나 정신질환을 앓을만큼 스승으로부터 배척을 당하게 된다.

'수학의 본질은 자유에 있다'는 명언으로 틀에 묶이지 않아야 함을 강조한다.

집합이란 무엇일까?

집합은 어떤 주어진 조건에 따라 그 대상을 분명히 알 수 있는 것들의 모임이다.

동물 이름 중 [고양이, 강아지, 쥐, 토끼, 병아리, 고슴도치, 기린, 사자, 말]이 있다면

그 중에서 이름이 세 글자인 동물을 모두 고른다면?

바로 고양이, 강아지, 병아리라고 말할 수 있다.

이것이 집합이라는 것이다.

그리고 집합을 이루고 있는 대상 하나 하나를 집합의 원소라고 한다.

즉, '이름이 세 글자인 동물들의 모임'은 집합이고 '고양이,강아지, 병아리'는 집합의 원소가 되는 것이다.

이것을 간단히 나타낼 수 있는 방법으로

우선 '이름이 세 글자인 음식들의 모임'에 속하는 모든 원소를 집합 기호 {   }안에 넣어 본다.

그리고 '이름이 세 글자인 동물들의 집합'을 A로 나타내보면

A={고양이, 강아지, 병아리}  가 된다.

원소의 갯수가 유한한 집합을 유한집합이라고 하고

원소의 갯수가 무한한 집합을 무한집합이라고 한다.

또한 유한집합 중에서도 원소가 하나도 없는 집합을 공집합이라고 한다.

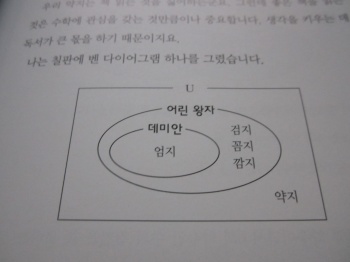
그렇다면 벤 다이어그램이란 무엇일까?

19세기 수학자 벤이 사용하기 시작한 것으로 벤은 수학자 이름을 뜻하고

다이어그램은 그림이나 표를 뜻하는 단어로서

집합을 알아보기 쉽게 여러가지 도형으로 나타내는 것을 말한다.

그림을 보면 개념이 들어서고 이해하기가 훨씬 쉽기 때문이다.

집합은 부분집합, 합집합, 여집합, 차집합, 전체집합이 있다.

일상생활에서도 이런 집합은 구분되어서 사용되기도 한다.

또한 칸토어처럼 고정관념을 버리고 생각의 폭을 넓게 사용할 수 있도록 해야한다.

그러기 위해서는 사물에 관심이 있어야 하고 끊임없이 질문이 수반되어야 하지 않을까 싶다.

갈릴레이가 들려주는 낙하이론 이야기

갈릴레이가 들려주는 낙하이론 이야기 ㅣ 과학자가 들려주는 과학 이야기 8
정완상 지음 / 자음과모음 / 2010년 9월

무거운 물체와 가벼운 물체가 같은 높이에서 떨어지는 데 같은 시간이 걸린다는 낙하이론을 책으로 만나볼 수 있다니 참 반가운 일이다.

갈릴레이의 낙하이론을 우리 주위에서 볼 수 있는 물건들을 이용해 직접 실험을 해 보면서 알아갈 수 있으니 흥미로움을 느끼게 한다.

이 책은 낙하이론과 속도의 개념을 느낄 수 있게 하는 것으로 설정되었다고 한다.

간단한 일상 속 실험을 통해 질문도 하면서 여러가지 운동과 낙하이론을 쉽게 설명한다니

목차를 쭈욱 훑어보면서 어떤 내용일지 궁금해진다.

그렇다면 먼저 속력이 무엇인지에 대해 알아볼 필요가 있을 것 같다.

즉 속력은 물체가 얼마나 빠른가를 나타내는 것으로 두루마리 종이에 봉을 끼운 후

일정한 속력으로 잡아당기게 한 후 비트 박스를 도입해서 일정한 울림에 따라

두루마리 종이에 신발을 올리게 한 실험을 하게 했다.

결국 속력의 개념과 일정한 속도의 운동 그리고 속도가 변하는 것을 알게 되었다.

또한 일정한 간격으로 움직이는 것을 평균 속력의 개념과 함께 연결지었다.

속도는 물체의 이동하는 속력과 방향을 말하는 것으로 좌표를 사용했다고 한다.

즉 물체의 빠르기 뿐 아니라 물체가 움직이는 방향까지 나타내는 양으로

변위를 나눈 값으로 정의를 한다고 한다.

이 부분에서는 공식이 적용되어 살짝 이해하기가 어려웠다.

물체의 속도가 변하는 경우 일정한 시간동안 속도가 얼마나 변하는가를 나타내는 것을

가속도라고 하는데 속도가 달라지는 것을 나타낼 때는 무엇을 이용해야 하는지 궁금하다.

속도가 더 증가하는 것이 아닌 속도의 변화를 말하는 가속도는

만약 속도가 변하지 않는다면 가속도는 0이라고 말할 수 있다는 것을 이해할 수 있었다.

정지해 있던 물체가 아래로 떨어지는 운동을 자유 낙하라고 한다.

갈릴레이는 물체의 질량과는 아무 관계없잎 같은 높이에서 떨어뜨리면 같은 시간에 바닥으로 떨어진다고 했다.

피사의 사탑의 실험에서 보았듯이 말이다.

또한 그네 운동에서처럼 경사면을 따라 내려오는 것을 그림으로 쉽게 설명해서

그네의 속력에 대해 쉽게 이해할 수 있었다.

관성과  관성계와 비관성에 대해서도 언급을 하면서 지구가 태양 주위를 도는 이유를 궁금해했다.

지구가 태양 주위를 돈다는 지동성을 천동성과 함께 비교하여 설명했다.

마지막 부분에서는 '아이가 줄었어요'라는 창작동화를 수록하여 갈릴레이의 이론에 대해

아주 재미있게 다뤄서 좀더 쉽게 접근할 수 있었다.

멘델이 들려주는 유전이야기

멘델이 들려주는 유전 이야기 ㅣ 과학자가 들려주는 과학 이야기 2
황신영 지음 / 자음과모음 / 2010년 9월

생물학에서 많은 과학자들이 어떤 식으로 유전이 되는지 명확히 밝히지 못할 때

멘델이 유전의 법칙을 발견함으로써 결국 유전학이라는 학문이 생기게 되었다고 한다.

몇해 전 한참 화제가 되었던 복제양 돌리나 배아 복제, 줄기 세포, 유전자 조작 등의 연구 결과는

멘델의 유전 법칙을 바탕으로 이루어진 하나의 사례가 아닌가?

목차를 보면 옛날 사람들은 어떤 유전적인 현상이 이루어졌는지를 궁금해 하면서 실험을 하고

결국 멘델의 가장 중요한 세가지 법칙을 발견하고

또한 계속되는 질문으로 답을 얻었다는 것을 알 수 있다.

유전이란 부모의 형질이 자손에게 전해지는 것을 말하는데

옛날 사람들은 자식들의 모습이 부모와 닮는다는 사실을 알고 있었기 때문에

동물과 식물의 유전에도 관심을 가지면서 자손은 어버이를 닮는다는 것을 알게 되었다.

그래서 우수한 품종을 얻기 위해 곡식의 씨앗 중 튼튼한 것만 골라 뿌리기도 했다.

완두콩 실험으로 유전에 대한 열성과 우성을 알려주며 식물이 어떻게 수정해서 유전되는지

식물의 생식기관을 통해 대립형질을 알아내었다.

이렇게 해서 멘델의 중요한 우열의 법칙, 분리의 법칙, 독립의 법칙을 알아볼 수 있다.

그렇다면 모든 유전현상에는 멘델의 법칙이 성립될지에 대한 의문이 든다.

사람의 유전 형질을 연구하는 데는 한 세대가 길기 때문에 시간이 오래 걸리고

자손의 수가 적어 통계를 내기도 어렵고 마음대로 교배할 수 없으며 환경에 차이가 날 수 있고

다른 생물보다 많은 유전 형질 때문에 어려움이 있다고 한다.

하지만, 현대과학에서는 멘델의 법칙을 바탕으로 유전병이나 알비노병, 혈우병 등의

어떤 형질이 유전되어 나타나는지에 대해 알려준다고 한다.

유전학에 어려움을 느꼈지만 이 책을 통해 유전 법칙을 이해하는데 도움이 된 것 같다.

플라톤이 들려주는 이데아 이야기

플라톤이 들려주는 이데아 이야기 ㅣ 철학자가 들려주는 철학 이야기 1
서정욱 지음 / 자음과모음 / 2005년 10월

철학은 학창시절 뿐 아니라 성인이 된 지금도 따분하고 지루하다고 느껴지는 한 분야인데요.

좀 쉽게 읽기 위해 한번 쭈욱 훑어봤어요.

머릿말에도 나와있지만 본문이 대화로 되어 있어 우선 지루하지 않게 볼 수 있었어요.

철학은 우리가 어떻게 살아야 하는지 무엇을 우선으로 해야 하는지

행복한 삶이 무엇인지를 알려주는 학문이라고 간단하게 정의를 내면서 플라톤의 철학을 다뤘어요.

플라톤이 가장 먼저 이야기를 한 것이 도덕이였어요.

사람이 살아가는 데 가장 필요한 것이지만 플라톤이 살았던 당시의 사람들은 도덕을 잘 몰랐고

교육을 통해 도덕을 배울 수 있다는 것도 몰랐다고 하네요.

플라톤은 이 도덕을 바탕으로 법의 중요성을 강조하면서 순수한 사랑에 대해 생각하기 시작했고

자신의 순수한 생각을 갖기 위해 무엇이 필요한지를 고찰하면서 이데아를 이야기했어요.

그리고 이데아를 찾는 것이 보물찾기와 비슷하다고 하면서 철학 수사대를 결성하여 책의 이야기를 시작하죠.

그들이 하려는 일이 '정의'라는 보물을 찾는다는 것이죠.

어떤 이야기가 펼쳐질지 궁금해지네요.

모험을 하는 듯한 흥미진진한 사건의 전개를 따라 이데아의 세계에 가니 조금은 이해할 듯도 하네요.

막연했던 이데아의 세계를 들여다보니 의외로 쉬운 듯 느껴져요.

이데아의 유령은 똑똑한 류팽을 데려가려 하지만 현실의 세계로 다시 돌아오면서

또 한번의 모험을 하게 되네요.

정의찾기 대회도 열리고 하나하나 사건을 해결해 가는 철학 수사대의 활약이 기대되네요.

이데아와 정의가 무엇인지 왜 플라톤이 이것을 강조했는지 알게 되었네요.

각 단원마다 철학돋보기의 내용이 다시 한번 정리해 주니 참 유익하더라구요..

책을 다 본 후의 통합형 논술문제도 책을 본 후의 시야를 넓혀 주는 계기가 되는 것 같아요.

철학은 지루하지 않다는 것을 보여주는 흥미로움과 해결사의 역할을 하면서 보니

아이들도 좀더 쉽게 접근할 수 있는 시간이였어요.

찰리가 엄마한테 혼날 땐 - 나랑 똑같아

찰리가 엄마한테 혼날 땐? ㅣ 지구별 창작 그림책 2
해리엇 지퍼트 글, 바루 그림 / 키움 / 2012년 9월

찰리가 엄마한테 혼날 땐? 과연 어떤 일이 벌어질까요?

표지에서도 느껴지듯 혼내고 혼나는 모습이지만 어둡지 않고 의외로 밝고 개구져 보이네요.

다섯 살 개구진 우리 아이도 늘상 엄마한테 혼나는 모습이기도 하고

오빠 장난감과 크레파스를 빼앗았다가 억울하면 울면서 동생을 혼내는 아들의 모습이 보이기도 하네요.

오호~~ 첫 장면부터 사뭇 기특한 모습으로 책을 읽어주는 모습이네요..

우리 아이는 이 모습을 보고는 자기가 동생한테 책 읽어주는 것과 같다고 말하네요.

제법 진지한 모습으로 책을 보기 시작했어요. 

악기를 연주하지만 동생이랑 둘이 이렇게 토닥토닥 거리는 모습과도 비슷하네요.

이렇게 병원놀이도 하면서 말이죠..

푸힛~~ 오빠가 다쳐서 밴드를 붙이면 동생도 괜스레 발이나 팔을 내밀며

아프다고 밴드 붙여달라고 떼를 쓰는데 이 장면을 보면서 자기가 동생한테 밴드 붙여줬다고

아주 자랑스럽게 얘기를 하네요.

그렇지만 결국 찰리가 엄마한테 혼날 땐 " 네 방에 가 있어"라는 말을 듣게 되죠.

그럼 찰리도 버니에게 똑같은 행동을 하죠..

"엄마랑 화나면 똑같아" 라고 씩씩 거리는 아들..

가끔 동생 때문에 억울하게 혼날 때도 있었기 때문에 그 감정이 남았나봐요..

찰리가 엄마한테 혼날 때는 찰리도 버니에게 생각하는 시간을 주죠..

찰리가 잘하는 말도 있고 지겨울 때도 싫을 때도 있지만 무서울 때는 버니를 꼭 껴안는다고 하네요.

언제 들어도 싫지 않은 '미안해'라는 말도 말이죠.

하지만 제일 포근하고 부드러운 건 '사랑'이란 것을 느끼고 배우게 된다네요.

저 역시도 아이를 혼낼때는 단호하고 무섭게 혼내지만 화를 다스리게 되면

'미안해. 사랑해' 라는 말로 아이를 안아주는데...

혼나고 나서 그 후의 행동이 아이에게 중요한 감정을 느끼겠구나 하는 걸 느꼈어요.

아이는 이 책을 본 후에 '나랑 똑같아' 라고 말하네요...

행동을 하기 전에 아이의 입장을 다시 한번 생각해 보게 되는 시간이였어요.