많은 분들이 동의하듯이 수학은 어렵습니다. 자연과 우주가 이야기하는 언어를 인간이 추상화한 학문을 수학이라고 한다면 그 언어는 인간이 진화하면서 자연스럽게 습득한 그것과는 다르다는 것을 추정할 수 있을 것입니다. 인간의 뇌는 그렇게 진화하지 않았음에도 불구하고 수학이라는 학문을 통해 자연과 우주의 이야기를 이해하려고 하니 당연하게도 어려울 것입니다. 자연과 우주를 이야기할 때 우리는 ‘인간의 언어’를 동원하여 설명하려고 합니다. 하지만 인간의 언어는 자연과 우주를 설명하는데 적합한 언어는 아닙니다. 그렇기에 ‘수’ 혹은 ‘수학’은 자연과 우주를 이해할 수 있는 거의 유일한 커뮤니케이션 수단입니다.
모두가 수학을 잘 해야 할 필요는 없겠지만, 그래도 우리에게는 ‘수학이 필요한 순간’은 언제나 존재합니다. 과거부터 수학이라는 분야는 전문가의 영역이었습니다. 전문가가 필요한 수학에서의 영역은 학문으로써 수학이 발전하면서 점차 확장되어 왔지만 일반인들 역시 수학에 점차 익숙해지고 있습니다. 한 예로 지금은 초등학생이라면 대부분이 쉽게 계산할 수 있는 사칙연산도 예전에는 수학 전문가들의 영역이었다고 합니다. 또한 현대인이라면 확률의 개념에 대해 이야기하고 이해할 수 있지만 확률 이론이 처음 제기된 17세기에는 전문 수학자들도 이해하기 어려운 분야였습니다. 앞으로 100년 후, 200년 후의 후손들은 우리보다 수학을 훨씬 잘 이해할 지 모릅니다.

김민형 교수 (1963~,전 옥스퍼드대 교수, 현 워릭대 수학대중화 석좌교수)는 지난 2018년 “수학이 필요한 순간 (인플루엔셜)”을 통해 우리에게 수학적 사고방식이라는 수단을 통해 인간이 얼마나 깊게 생각할 수 있는지에 대해 우리에게 이야기를 들려준 바 있습니다. 이번에 새롭게 출간되는 “다시, 수학이 필요한 순간 (김민형 著, 인플루엔셜)”을 통해 김민형 교수는 ‘질문은 어떻게 세상을 움직이는가’라는 주제로 8강에 걸쳐 또다시 수학에 대해 이야기를 들려주려 하고 있습니다.
먼저 연령도 직업도 다양한 수포자들의 ‘수학’에 대한 대화가 눈에 들어옵니다. 아마 전작의 세미나 과정에 참여하였던 분들과의 대화를 책으로 엮은 내용인 것 같은데 많은 이야기들이 공감되었고 특히 ‘수학은 언어’라는 부분은 항상 제가 생각하던 부분과 딱 맞아 떨어지는지라 반갑기까지 했습니다.
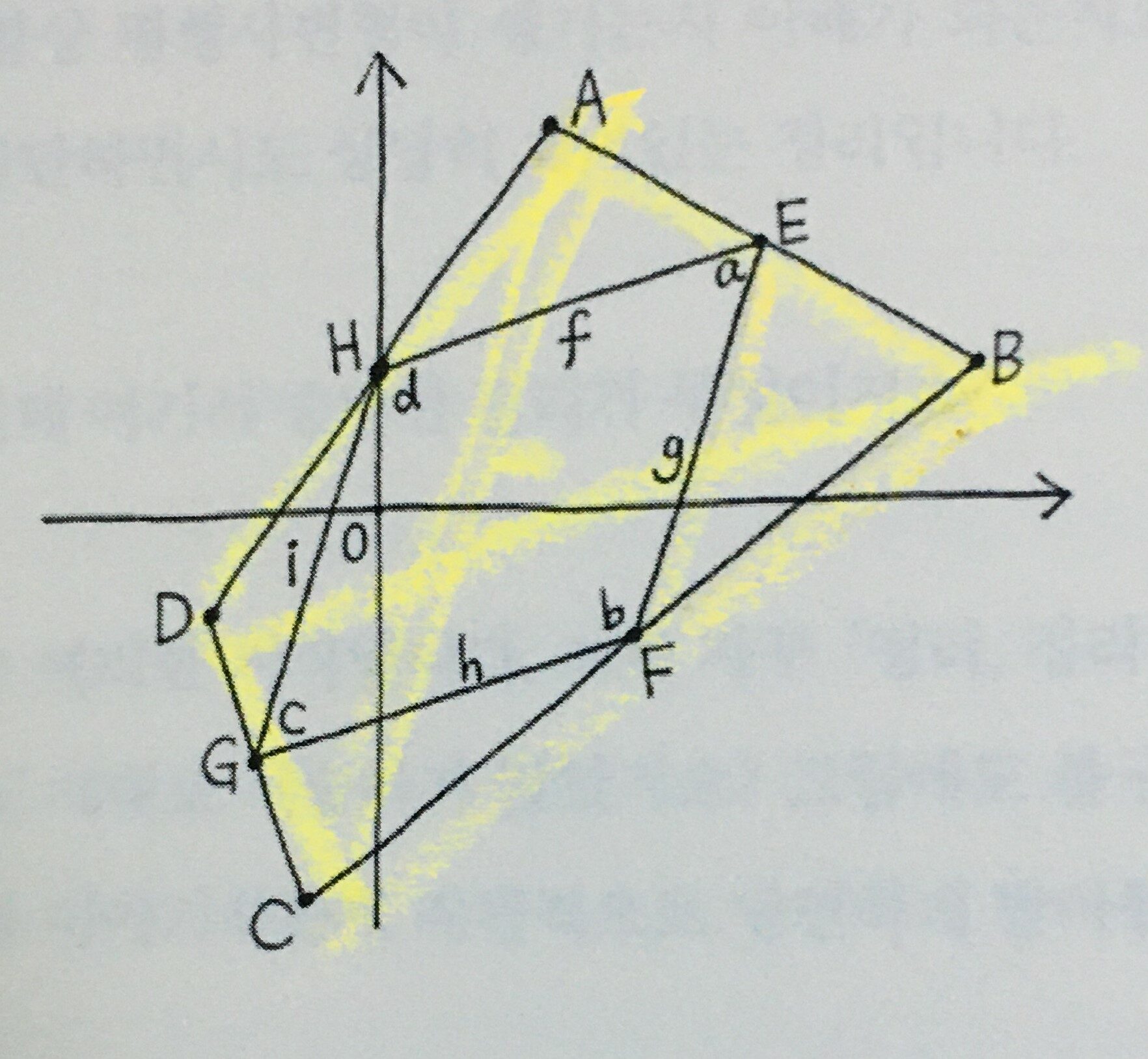
‘바리뇽의 정리’에 대해 보조선을 활용하여 증명하는 방법을 설명하면서 ‘눈에 보이지 않는 것을 떠올려 스스로 발견’하는 수학적 창의성은 간단하면서도 재미있는 예시였습니다.
공리, 정리 등의 개념을 정립하는 과정에서 ‘수학이 확실하지 않을 수’도 있다는 점에서는 다소 충격을 받았습니다. 이 부분은 공리체계에 대한 개념인데 자세한 것은 책을 통해 확인바랍니다.
‘수의 위기’에 대한 이야기도 재미있기도 하고 생각할 부분이 많았습니다. 특히 ‘모든 것은 수’라고 믿었던 피타고라스가 수가 아닌 수, 즉 무리수를 발견 혹은 재발견했을 때의 충격, 그리고 이로 인해 이어진 유럽에서 기하학에서 ‘수’가 사라져간 이야기 등은 신기하기도 하고 재미있으면서 수학의 불확실성에 대한 확실한 사례이기도 하였습니다.
‘디오판토스 방정식’은 저자에 따르면 '좀 유치하게 보이지만 수학의 모든 분야에 교묘하게 줄기와 가치를 펼치고 있는 이론'인데 이를 통해 기계적으로 판별할 수 있는 알고리즘은 없다는 것을 설명합니다. 즉, ‘수학적인 활동 속에 알고리즘이 차지하고 있는 부분이 굉장히 적다’는 사실을 보여주는 사례인데 수학적 정리의 상당 부분을 알고리즘으로 해결할 수 있다는 일반 상식 혹은 믿음에 반하는 사례라 놀라웠습니다.
수학은 수천년간의 전통과 체계적 사고가 겹겹이 쌓인 학문 체계입니다. 그러므로 그러한 학문 체계를 받아들이기 위해서는 기초를 쌓아 올리고 체계 내에 편입하려는 노력이 필요한데 저자는 이걸 기초 기술을 습득하고 반복 훈련을 하여 익숙해지면 다음 단계로 올라가다 어느 경지에 이르면 자유롭게 연주를 할 수 있는 피아노에 비유합니다. 피아노는 그런 훈련을 당연하게 생각하지만 수학은 그렇지 않아 유독 어렵다고 생각하는 것이 아닐까요?
책에는 어렵거나 이해하기 어려운 내용도 있습니다. 하지만 팟캐스트 강의에서 들었던 김민형 교수의 말투가 떠오르는 문장으로 조곤조곤 설명해주고 있어 재미있게 읽다보니 어느덧 다 읽게 되었네요. 제가 읽은 것은 총 4강까지만 묶은 가제본이라 정식 출간본을 통해 나머지 4강의 내용도 읽었으면 합니다.
#다시수학이필요한순간, #김민형, #인플루엔셜, #질문은어떻게세상을움직이는가
※ 출판사로부터 가제본을 제공받아 작성한 리뷰입니다