초재밌어서 밤새읽는 수학이야기

초 재밌어서 밤새읽는 수학 이야기 ㅣ 재밌밤 시리즈
사쿠라이 스스무 지음, 김정환 옮김, 계영희 감수 / 더숲 / 2014년 1월

수학을 전공하여 수학의 역사와 수학자의 삶을 전하는 강연을 하는 일본인이 쓴 수학에 대한 책이다.

학문적인 수학이 아닌 재미로 읽을 수 읽으면서 수학의 매력을 느낄 수 있게 기술된 책이다.

가볍게 읽을 수 있는 수학 교양 서적이다.

제목에 '초' 라는 말이 있어서 초등학생용을 의미하는 줄 알았다.

그건 나의 착각이었고, 수학에는 초공간, 초기하급수, 초월수 등 '초'가 붙는 용어가 많은데, 그 공통된 특징은 '엄청나다'라는 것이라고 저자는 말하는데, '초 재밌었어서' 라는 말은 '엄청나게 재밌어서' 라는 의미였다.

내가 읽어보니 초등학생이 읽기에는 조금 어려운 내용이 있긴 했지만, 일부 내용들은 초등학생들에게도 수학적 흥미를 줄 수 있는 내용들이었다.

책의 시작은 도박이야기로 시작한다.

도박에 관심이 별로 없는 나에게는 그다지 흥미롭지는 않았다.

그 다음에 나오는 미인각에 대한 이야기부터는 재미를 느끼기 시작했다.

마릴린 먼로, 모나리자와 같은 미인들의 얼굴은 양쪽 눈썹과 입술의 양쪽 끝을 연결한 두 선이 이루는 각도가 45도 라고 한다.(p.31)

저자는 이 45도를 미인각이라고 불렀다.

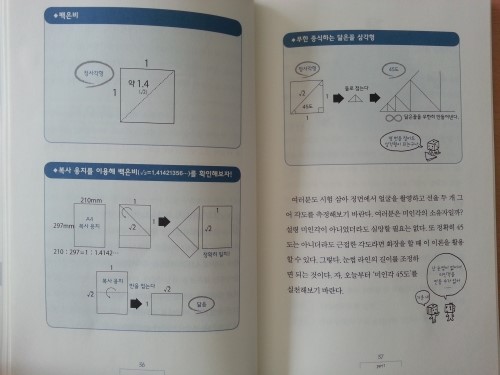
미인각은 정사각형이나 백은비(silver ratio)와 관계가 있다고 한다.

백은비는 1대 √2의 비이다.

정사각형의 한변과 대각선이 이루는 각도인 45도는 미인각, A4용지에서 발견할 수 있으며, 무한증식하는 달은꼴 삼각형을 그리는데서도 발견할 수 있다.

쉽게 생각할 수 있는 대상에 수학적 의미를 심어주는 내용을 보면서 수학에 대한 흥미와 관심이 유발되는 효과를 얻을 수 있었다. 

전자계산기를 이용한 마술트릭도 재미있었다.

실제로 아이들에게 시도해보면서 마술 흉내를 내기도 하였다.

12345679×□×9=□□□□□□□□□

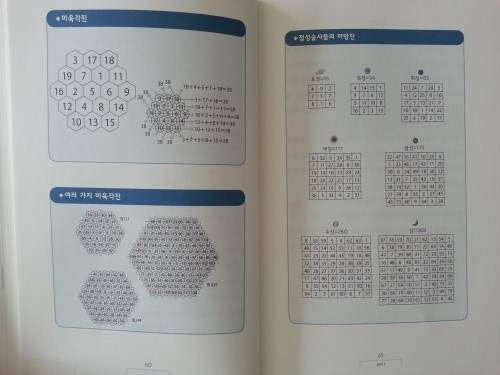
마방진 내용은 참 신기하다.

마방진은 n×n의 칸에 적힌 숫자를 가로, 세로, 대각선 등 어느 방향으로 더해도 그 합이 똑같아지는 신기한 도형이다.

많은 사람들이 마방진을 풀어냈다는 것이 참 신기하게 느껴졌다.

사람들의 관심 분야는 정말 다양하다는 생각이 들었다.

16세기에 점성술사들의 마방진을 사람들이 부적으로 삼았다고 한다. 

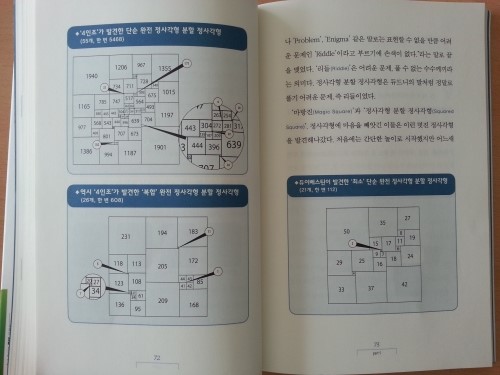
정사각형 분할 정사각형에 몰입한 수학자들의 이야기도 재미있다.

정사각형을 전부 다른 크기의 정사각형으로 겹치거나 비는 공간 없이 메울 수 있을까?

러시아의 수학자 루진이 제기한 질문으로 루진의 문제라고 불리운다고 한다.

이것을 풀기 위해서 노력한 수학자들이 정말 대단하다는 생각이 들었다.

수학자들은 정사각형에 왜 매달렸을까?

정사각형 분할 정사각형에 대한 해답 발견의 성과는 어떤 유익함이 있었을까?

이러한 나의 궁금증에 대한 답변이 이 책에 기술되어 있지는 않아서 조금 아쉬웠다.

정사각형이 피타고라스의 정리와 페르마의 최종 정리와 연관되어 있다는 설명이 나왔다.(p.74)

단순 완전 정사각형 분할 정사각형의 최소 개수는 21개로 1978년에 네덜란드의 듀이베스틴이 발견하고 증명했다고 한다.

참으로 대단하다.

윤년은 4년에 한번 2월 29일이 있는 1년이라고 말한다.(p.77)
윤년이 있는 이유는 1년이 365일이 아니고 365.2422일이기 때문에 4년마다 하루를 늘려서 0.2422일의 오차를 줄이기 위한 것이라고 한다.

이 책에서 친절하게 설명해주어서 윤년에 대한 수학적 의미를 알 수 있었다.

4의 배수인 해를 윤년으로 삼는다는 규칙만으로는 시간의 오차를 해결할 수가 없어서 100의 배수이며 400의 배수가 아닌 해는 윤년으로 삼지 않는다라는 규칙이 있다고 한다.

A와 B라는 두 사람이 카드 13장씩을 가지고 책상 위에 한 장씩 내놓으면서 짝 맞추기를 할 때 같은 숫자의 카드가 동시에 나오는 만남이 한 번도 일어나지 않을 확률은 37%라고 한다.(p.93)

n을 무한대로 늘려도 약 37%에 수렴한다는 것을 오일러 수학자가 발견했다고 한다.

반대로 만날 확률은 63%가 된다.

남녀의 만남에서도 쇼핑에서도 마음에 드는 상대를 만날 확률은 63%라고 말한다.

인생에서 행운의 확률은 50 대 50이 아니라 60 대 40이라고 생각할 것을 조언한다. 

0으로 나누면 왜 안될까에서 평소에 우리가 그냥 암기하여 알고 있던 내용을 깔끔하게 정리해준다.

3÷0=? → 0×?=3 → 이것을 만족하는 ?는 없다. 따라서 3÷0 의 답은 없다.

그리고, 0÷0 의 답은 무수히 많다는 것을 보여준다.

0÷0=? → 0×?=0 → 이것을 만족하는 ?는 무수히 많다.

0 제곱을 하면 왜 1이 될까에 대해서도 친절하게 설명해준다.

나는 그냥 0 제곱을 하면 1이 된다고 암기를 했던 것 같다.

2의 제곱 지수 부분에 주목하면 5, 4, 3, 2, 1로 지수가 1씩 작아질 때마다 우변의 값이 ½배가 작아진다.

지수법칙을 이용해서도 설명을 해준다.

미터와 킬로그램의 탄생에 대한 이야기도 재미있었다.(p.170)

1891년에 프랑스 과학자들이 파리를 통과하는 적도에서 북극까지의 길이를 측정해 그 1천만분의 1을 길이의 기준으로 삼기로 결정했고, 자오선(북극과 남극을 연결하는 선) 전체 둘레의 4천만 분의 1을 1미터로 결정했다고 한다. 
1미터는 지구의 둘레 길이를 바탕으로 결정되었고, 10cm 인 정육면체의 부피를 1리터로 결정하였고, 최대 밀도 온도 4℃인 증류수 1리터의 무게를 1KG으로 결정되었다고 한다.

한자속에 숨어있는 숫자에 관한 이야기, 수학을 찬양하는 명언들, 가장 큰수와 가장 작은수를 어떻게 표현하는지에 대한 이야기, + 와 - 와 × 와 ÷ 의 발생 기원에 대한 이야기, 푸앵카레 추측과 증명한 수학자에 대한 이야기, 커다란 숫자를 읽는 법에 대한 내용들이 기술되어서 재미를 주고 있었다.

저자는 책 맺음말에서 '계산은 여행이다'라고 말한다.

서로 다른 세계, 서로 떨어진 세계 사이에 등호라는 다리를 놓는 것이 수학자의 임무이고, 계산 여행을 계속할수록 새로운 세계를 만나게 된다고 말한다.

수학에 대한 상식과 역사, 수학의 재미와 수학자들의 위대함을 쉽게 다가서며 배우게 해주는 책이었다.

그동안 입시를 위한 도구로써 배워왔던 수학을 우리 일상 생활과 밀접한 친숙한 학문 그리고 재밌고 신기한 학문으로 다시 느끼게 해 준 책이다.