우리 나무 꽃 50가지에 숨은 비밀을 찾아 꽃 탐험에 나서다! ‘나무 꽃의 비밀‘

나무 꽃의 비밀
신영준 지음 / 지성사 / 2022년 9월

나무 꽃의 비밀

<지성사>

주위를 둘러보면 꽃들도 종류가 참 다양하게 많다는 걸 나이가 들면서

알아보게 되었답니다.

아이들과 단지에서 혹은 차를 타고 다니며 보게 되는 꽃은

인터넷으로 꽃이름을 찾아볼 정도로 관심이 생기더라고요.

아이들에게 꽃에 대해 설명을 해주면

아이들도 진지하게 듣고 곧잘 기억하기에

<나무 꽃의 비밀>도 아이들과 함께 읽었어요.

꽃 설명중 꽃이 들어간 노래들이 나오는데

엄마가 불러주며 노래 속에 나오는 꽃이 이 꽃이라고 설명을 해주니

더 잘 듣더라고요.

 

우선 꽃이름을 알기 전에 '꽃'의 구조와 관련 용어를 알아봤어요.

가루받이, 갈래꽃과 통꽃, 거, 꽃대, 꽃받침, 비늘줄기, 설상화와 통상화 등등

사진과 그림을 통해 자세히 배울 수 있었습니다.

 

모두 50가지의 꽃들이 소개되어 있어요.

 

봄이 되면 여기저기서 볼 수 있는 꽃 '매화나무'입니다.

'봄의 전령' 매실나무라고 소개되어 있는데 '봄의 전령'이라는 단어가 참 예쁘고 잘 어울린다 싶었어요.

장미과이며 2월에서 4월 사이에 볼 수 있는 꽃이에요.

본문에 <매화를 보면 누구나 시인이 되고 누구나 화가가 된답니다>라고 시작하는데

한줄 한줄 읽어나가며 '지식'만 얻는게 아니라 멋진 표현도 배울 수 있었습니다.

피로 해소의 음료수로 잘 알려진 <매실>이 바로 이 매화나무의 열매랍니다.

매화의 한자어인 梅에는 신맛이 난다는 의미도 있는데

어머니를 뜻하는 어미 母가 포함되어 있어요.

어머니들이 아이를 잉태하면 신 것이 먹고 싶고,

그 신맛을 제공하던 것이 매실이어서 매실나무라는 이름이 붙었다고 합니다.

 

그런데 이 매화와 꽃 모양이 비슷한 식물이 있어요.

살구나무와 벚나무이랍니다.

매실나무, 살구나무, 벚나무를 구별하기란 사실 쉽지 않다고해요.

이 책을 통해 서로 다른 점을 배워볼까요?

 

두번째 소개해드릴 꽃은

제가 작년에 알게된 '이팝나무'라는 거에요.

옆지기의 발령으로 대구에 2년 내려갔다 왔는데

대구에는 정말 이 꽃들이 정말 많더라고요.

흰 쌀이 다닥다닥 붙어 있는 모양이라 이팝나무라고 불리었다는 이 꽃나무는

물푸레나무과이며 4월에서 5월에 만나 볼 수가 있어요.

하늘에서 쌀이 내려오게 한다는 이팝나무.

사실 이 꽃나무는 경북 남부에서 전북을 한계선으로 남부 지방에서 주로 자랐는데

기후 변화의 영향으로 중부지방에서도 볼 수 있게 되었대요.

조선의 이씨 왕조에서 벼슬을 해야 쌀밥을 먹을 수 있다 하여

이씨가 세운 조선 왕조의 쌀밥 → 이밥 → 이팝이라는 이름이 붙었다는 이야기가 있고,

또 다른 이야기로는 24절기 중 하나로 여름이 시작된다는 입하 무렵에 꽃이 피어

입하 → 이팝이 되었다는 이야기도 있어요.

경상도에서는 쌀밥을 이밥이라고 했는데

이밥에 맺힌 한으로 죽은 며느리의 넋이 변해서 핀 꽃이라 이밥나무가 되었다는 이야기도 있는데

세가지 이야기중 어느 이야기가 가슴에 가장 와닿으시나요?

 

아까 기후 변화로 이제 중부지방에서도 만나 볼 수 있다고 했잖아요.

서울시 가로수의 6.5%로 다섯 번째로 많이 심어졌다고 해요.

우리가 이팝나무를 쌀로 볼 떄 서양에서는 하얀 '눈'으로 보았다고 해요.

같은 꽃을 서로다르게 보는 것도 참 신기하네요.

 

모든 꽃나무 이야기 끝에는

'비밀 속으로'가 있는데

<이팝나무처럼 수꽃과 암꽃의 기능에 따라 구분을 하는 것은 이팝나무에 어떤 이점이 있을까요?>

처럼 질문을 통해 좀더 꽃나무에 대해 깊이 있게 설명을 해줍니다.

비밀을 들여다 보기 위해 188쪽으로 이동해보니

이팝나무에 주는 이점은 바로 유전적인 다양성을 가지도록 도와준다고해요.

50가지의 꽃나무에 대한 '비밀의 문'을 열어 많은 걸 배워봤습니다.

고개를 돌리면 사방에서 마주치는 우리 나무 꽃 50가지의 모양과 이름,

이름의 유래, 생존 방식 등을 보면서

식물의 비밀 속으로, <나무 꽃의 비밀>을 통해 들어가봐요!

#책세상 #맘수다 #나무꽃의비밀 #신영준 #지성사 #식물이야기꾼 #이팝나무 #매화나무

˝무슨 그런, 아들 가슴 찢어 놓는 말씀 하세요!˝

[전자책] 미분과 적분 : 뉴턴의 대발명 - Newton Highlight 48 ㅣ 뉴턴 하이라이트 Newton Highlight 48
일본 뉴턴프레스 엮음 / 아이뉴턴(뉴턴코리아) / 2017년 8월

Newton

HIGHLIGHT 48

뉴턴의 대발명

미분과 적분

중2, 3인 아이들이 좋아하는 과학 잡지 <Newton highlight>이예요.

뉴턴 잡지는 <뉴턴>과 <뉴턴하이라이트>로 나누어져 있는데

<뉴턴>은 중고등학생들뿐만아니라 과학을 좋아하는 성인들에게도 추천해주고픈

수준 높은 과학잡지이고,

<뉴턴 하이라이트>는

월 잡지 <뉴턴>에서 주제별로 하이라이트를 모아 발간한 잡지랍니다.

중2, 3인 아이들이 고등 수학을 하고 있다보니 관심이 많은 미분과 적분.

고등학교에 가면 배워야 할 미적분을 저는 너무 어렵게 이해했었기때문에

미적분에 관련된 도서를 구입해 많이 읽고, 개념을 이해해보게 했었었어요.

미적분이 수학에서 배우는 개념이지만

사실 어디에 적용되는지는 잘 모르는 경우가 많잖아요?

저도 고등학교때 교과서에 있으니깐 배운거고

미분과 적분 하는 법은 알지만 어디에 이용되는지는 모르고 있었답니다.

아이들과 책을 통해 배우면서 알게 되었는데

그 미분과 적분을 완전히 쉽게 설명해주고 있는 책을 찾았어요.

바로 <Newton highlight 48 뉴턴의 대발명 미분과 적분>이랍니다.

뉴턴, 라이프니츠, 페르마 등 유명한 과학자의 이야기도 중간중간 함께 설명해주고 있어서

전혀 지루하지 않게, 오히려 재미있게 읽을 수 있었습니다.

중등이들은 벌써 3~4번 반복해서 읽었대요.

전 이제 한번 읽었는데 진짜 너무 재미있어요.

과학이나 수학을 좋아하는 중,고등학생들뿐만아니라

성인들에게도 추천해드리고픈 책이예요.

 

Newton highlight

뉴턴의 대발명 _ 미분과 적분

미적분의 탄생 전야, 뉴턴의 미분법, 미분과 적분의 통일,

미분과 적분의 발전 배경, 심화 지식편

140페이지에 재미있는 미적분이야기가 그득그득 담겨있답니다.

기말고사 준비중인 중2, 3인 아이들이 이번 겨울방학때 읽지 못했던 <뉴턴 하이라이트>를

구매해 달라고 해서 어떤 주제를 고를지 고민중이에요.

뉴턴 홈페이지에서 과월호를 쉽게 주문할 수가 있더라고요.

읽고 싶은 주제의 책들을 골라 겨울방학내내 읽을 계획을 벌써부터 세우고 있는 중이랍니다.

 

미적분이란?

간단히 말하면 사물이 어떻게 '변화'하는지를 계산하는 수학이에요.

예를 들면, 던져진 공의 속도를 알면, 그 공이 몇 초 뒤에 어디를 어떤 속도로 날아 갈지 계산 할 수가 있는거지요.

미적분을 이용하면 '미래'를 예측할수가 있는 거지요.

우리의 일상생활 속에서 미적분을 이용할 일은 없지만

우리가 누리는 물질문명의 혜택은 미적분의 도움 없이는 존재할 수가 없었어요.

지진을 견디는 강도, 비행기의 적절한 날개 크기, 경제 상황변동, 우주선의 궤도 등등을

계산하는데 바로 미적분이 필요한 것이랍니다.

 

미적분의 창시자 모습이에요.

누구인지 아시겠어요?

바로 이 잡지의 이름과 같은 '뉴턴'이랍니다.

미적분을 23세 나이에 발명한 천재이죠!

뉴턴은 미적분말고도 여러 '공식'을 정리해준 과학자이기도 하지요.

대학시절 페스트때문에 집으로 돌아온 뉴턴은 시골의 조용한 환경에서

과학사를 빛나게 하는 세 가지 커다란 발견을 해요.

미적분, 만유인력의 법칙, 빛의 이론.

과학사를 빛낸 1665년과 1666년은 나중에 '경이의 해'라고 불리운답니다.

그때, 뉴턴이 23세였다고해요.

미적분학이 영어로 calculus,

뉴턴이 방광의 결석으로 세상을 떠났는데 결석이 영어로 똑같이 calculus 라는 것도

참 신기하더라고요.

 

'1장 미적분의 탄생 전야'에서는 뉴턴에 의해 미적분이 탄생하기까지

이루어졌던 선배 과학자들의 발견을 소개해주고 있어요.

 

 

갈릴레이, 데카르트 그리고 페르마의 초상화들이에요.

우리가 모두 잘아는 과학자들의 모습이지요.

사진만 보고도 과학자 이름을 맞히는 아이들보고 놀랐어요.

사실, 페르마는 미적분하그이 창시자라고 일컬어지는 뉴턴과 라이프니츠에 앞서

미적분법의 요점을 몇 가지 밝혀 냈지만

'미적분의 기본 정리'에는 도달하지 못했기 때문에 미적분의 '창시자'라고 불리지는 않는다고해요.

페르마 입장에서는 살짝 아쉬울 것 같아요.

 

'2장 뉴턴의 미분법'에서는 뉴턴이 접선 문제를 해결하기 위해 어떤 것을 생각했는지

또 미분법이 어떻게 만들어졌는지에 대해 알아봅니다.

 

 

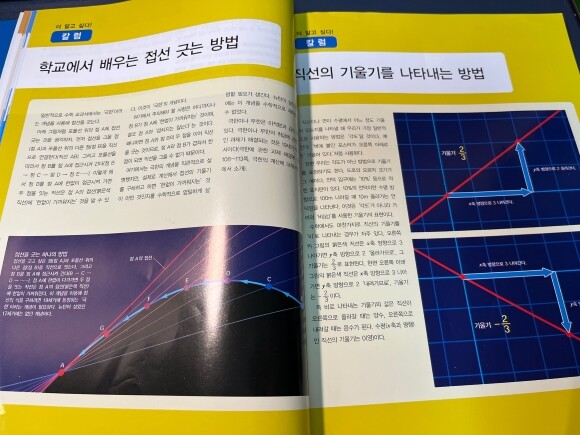
미분법에서 쓰는 기호, 읽기, 의미가 나와있어요.

저는 반가웠고, 아이들은 새로웠죠.

이렇게 개념을 접하면 고등학교에서 배우는 미적분에 대해 보다 어렵지않게 이해할 수가 있을 것 같아요.

 

'3장 미분과 적분의 통일'에서는 미적분이 하나가 되는 모습을 살펴볼 수가 있어요.

미분법이 곡선의 접선 기울기를 구하는 방법이고,

적분법은 곡선에 둘러싸인 영역의 넓이를 구하는 방법을 말해요.

고대 그리스에서 유래한 적분법과 뉴턴이 완성시킨 미분법이 뉴턴에 의해 통일되는

모습을 다루고 있습니다.

 

 

미적분에 의한 계산 그대로 찾아온 핼리 혜성 이야기는 살짝 감동이였답니다.

뉴턴이 만든 미적분이 미신이나 신비주의를 타파하고 그 정확성과 위력을 확인시킨 순간이었다고해요.

 

 

 

4, 5장에서도 미적분에 관한 재미난 그리고 깊이있는 이야기와 지식들을 배울 수가 있었습니다.

이해하기 어려운 딱딱하게만 느껴지는 과학을 그림으로 쉽게 설명해주는 '뉴턴 하이라이트'

과학에 좋아하는 중, 고등학생들에게 그리고 성인분들에게

정말 강추하고픈 과학잡지에요.

<출판사로부터 도서를 제공받아 직접 읽어보고 쓴 리뷰입니다>

곤충 탐구 추리 동화 [곤충 탐정 정브르]

곤충 탐정 정브르 2 - 장수풍뎅이 유령의 의뢰 ㅣ 곤충 탐정 정브르 2
도니패밀리 그림, 한바리 글, 샌드박스 네트워크 감수, 정브르 원작 / 서울문화사 / 2022년 10월

곤충 탐정 정브르 ②

장수풍뎅이 유령의 의뢰

<서울문화사>

여전히 곤충을 좋아하는 막내가 요즘 즐겨읽는 '정브르'의 이야기입니다.

정브르는 123만 구독자를 보유한

곤충과 파충류부터 바다생물까지 다양한 생물을 소개하는 생물 전문 크리에이터라고 해요.

브르와 고나는 장수말벌 부부가 보낸 초대장을 받고 곤충 세계로 떠나

장수말벌 부부의 실종된 막내 비비를 찾아주며

언제든지 곤충 세계에 올 수 있는 '만능 초대장'을 받게 됩니다.

그 후부터 브르와 고나는 곤충 세계에서 탐정 활동을 하고 있어요.

여기까지가 지난 1편의 내용이었고, 이제 2편 <장수풍뎅이 유형의 의뢰>를 소개해 볼게요.

 

2권에서는 두 개의 사건을 다루고 있어요.

1장. 장수풍뎅이 유형의 의뢰

2장. 폭탄 방귀 테러 사건

등장인물은 앞에서 소개해 드린 것처럼

세상의 모든 생물을 사랑하는 생물 유튜버 정브르와

만능 가방을 가지고 브르를 도와주는 강아지 고나랍니다.

 

1장 장수풍뎅이 유령의 의뢰

 

지난밤 브르의 꿈에 나타나 억울하다며 울던 장수풍뎅이 푸푸가 걱정된 브르와 고나는

'만능 초대장'으로 곤충 세계를 찾아갑니다.

 

"애들아 혹시 장수풍뎅이 푸푸를 아니? 우린 푸푸를 찾으러 곤충 세계에 왔어"

"푸푸라면.. 수액을 잘 찾는 녀석?

그런데 겁이 많아서 수액 자리를 항상 왕사슴벌레에게 뺏기지 않았어?

싸우지도 않고 말이야."

말하기가 무섭게 브로와 고나앞에 나타난 왕사슴벌레.

다른 곤충들은 왕사슴벌레가 푸푸와 앙숙관계라고 말해주었어요.

좀 더 단서를 찾으러 가다 죽어 있는 푸푸를 발견하게 되었습니다.

죽은 푸푸는 자신의 억울한 죽음을 해결해달라고 브르의 꿈속으로 찾아 간 거였어요.

책 속에 대화가 많이 이어지는데

대화 앞에 누가 한 말인지 그림으로 브로나 곤충들의 그림이 나와있어서

쉽게 이해할 수 있고, 더 재미있게 읽을 수 있었어요.

학습만화에서 자연스럽게 글밥으로 넘어가도록 도와주는 재밌는 책을 찾는다면

'서울문화사'의 <곤충 탐정 정브르>를 추천해 드리고 싶어요.

곤충 탐구 추리 동화라는 설명답게 '추리' 이야기가 궁금해

책장 넘기는 것을 멈출 수가 없었거든요.

글밥으로만 이루어진 책이 아니라 책 속에 그림이 은근히 많아요.

글밥과 학습만화가 반반 섞인 책이라

글밥을 힘들게 읽는 초등학교 중간 학년이나 책을 좋아하는 초등 저학년들도

재미있게 읽을 수 있는 책이라 생각합니다.

저희 막내는 5학년인데 워낙 '곤충'을 좋아해서인지

재미있게 그리고 아주 빠르게 읽어나가더라고요.

곤충을 좋아하는 초등 친구들에게도 추천해 주고픈 책이에요.

다시 이야기로 돌아와서

죽은 푸푸의 시체에서 브로가 단서를 찾았어요.

단서 1. 휘어진 뿔

단서 2. 가슴에 난 자국

단서 3. 뒤집힌 몸

정작 푸푸는 자신이 어떻게 죽었는지 전혀 기억을 못 하고 있어요.

그래서 브로와 고나 그리고 푸푸는 용의자들을 찾으러 곤충들에게 다시 가보았어요.

 

용의자는 셋!

다람쥐 포리와 왕사슴벌레 그리고 수컷 장수풍뎅이 차차

이렇게 셋으로 좁혀졌습니다.

 

이야기 중간에 이렇게 재미난 '다른 그림 찾기'도 있어요.

글을 읽다가 깜짝 놀랐네요.

그래도 찾아봐야겠죠?

도토리 수가 다르고, 꽃의 색깔이 다르네요.

브로가 머리에 무언가가 있고 없고... 누워있는 장수풍뎅이의 다리 수가 달라요.

자.. 이제 남은 두 곳은 여러분이 찾아보세요.

 

푸푸는 수액 냄새가 나는 곳을 찾아가다 먹는데 정신이 팔려

실수로 발을 헛디뎌 나무에서 떨어져 뒤집혔는데..

그 상태로 며칠간 배고픔에 허덕이다 죽었다는 거예요.

그런데 배고픔보다 더 괴로웠던 것은 그리운 친구, 토토를 못 보고 죽는다는 거였대요.

그럼 토토와 푸푸 사이에는 무슨 일이 있었던 것일까요?

흑.. 너무 감동적인 이야기였어요..

 

1장의 이야기 끝에는 '브르의 곤충 탐구 파일'로

곤충들에 대해 좀 더 자세히 배울 수가 있었답니다.

딱정벌레와 곤충의 더듬이에 대해

그림을 더해 설명을 해주고 있어서 어렵지 않게 이해했답니다.

 

2장은 폭탄 방귀 테러 사건인데 과연 어떤 내용일까요~

곤충 세계의 사건을 해결하는 브르와 고나의 이야기!

아이도 저도 무척 재미나게 읽었습니다.

<출판사로부터 교재를 제공받아 직접 읽어보고 쓴 리뷰입니다>

[100자평] 루이스 헤이의 365일 긍정 확언 일력

루이스 헤이의 365일 긍정 확언 일력
루이스 L. 헤이 지음 / 센시오 / 2022년 10월

매일 ‘오늘‘ 나에게 선물하는 ‘루이스 헤이‘의 가장 좋은 한마디. 그 말에 힘을 얻고, 위로를 받을 수가 있어요. 화려하지 않은 그림이 눈길이 더 가고, 여백에는 나의 말을 써봐도 좋을 것 같아요.

​

오늘 나에게 선물하는 가장 좋은 한마디 ‘루이스 헤이의 365일 긍정 확언 일력‘

루이스 헤이의 365일 긍정 확언 일력
루이스 L. 헤이 지음 / 센시오 / 2022년 10월

 

오늘 나에게 선물하는

가장 좋은 한마디

루이스 헤이의

365일

긍정 확언

일력

<센시오>

신비로운 느낌의 보라색 상자를 열면

며칠 동안 기다렸던 <루이스 헤이의 365일 긍정 확언 일력>이 들어있어요.

 

두꺼운 지지대가 있어서 쉽게 쓰러질 것 같지 않아 보이더라고요.

단단함이 참 마음에 들었어요.

내년에 고등학생이 되는 큰아이의 책상에 두고

아이가 매일 한 장 한 장 넘기며 '긍정 마음'을 받기를 바라는 마음에

아이에게 선물해 주었습니다.

글 읽는 걸 좋아하고 살짝 감성적인 아이가

열어보더니 마음에 쏙 들어 하더라고요.

뜯는 일력을 책상에 두고

매일 하루가 다 갈 무렵 뜯어서 뒷장에 일기를 써서 모아놓는 아이라

<루이스 헤이의 365일 긍정 확언 일력> 또한 마음에 들어 할 것 같았어요.

작가 '루이스 헤이'는 미국의 대표적인 심리치료사이자

베스트 셀러 작가, 헤이하우스 설림자이자 회장으로 상담가,

강연자, 교사로 활동했으며

불우한 삶 속에서 자기 자신을 사랑하고 인정하는 심리치료법인

'미러 위크'를 실천하여

자신의 삶을 치유로 이끌었다고해요.

전 세계 수많은 사람의 내적 성장과 치유를 도운 '루이스 헤이'가 해주는

한 마디 한 마디에 귀 기울여 봅니다.

 

나를 사랑하고 위로하는 열두 달.

각각의 달마다 주제가 있네요.

고등학생이 되는 저희 아이가 매일 일력에 쓰여있는 글귀를 보고

스스로를 '사랑'하며 공부에 지치는 날은 '위로'받을 수 있기를 바라봅니다.

 

JANUARY

나에게 사랑한다고 말하기

우리가 하는 모든 말과 생각은 하나의 암시입니다.

그중에서도 가장 강력한 암시는 거울 앞에서

내 눈을 바라보고 말하는 것입니다.

거울 앞에 서서 나와 만나는 것으로

하루를 시작해 보세요.

하루 한 번 나에게 건네는 한마디를 통해

나를 다시 사랑하게 될 거예요.

살면서 어떤 문제를 겪게 되더라도,

최선의 해결책은

언제나 나 자신을 사랑하는 것입니다.

루이스 헤이의 365일 긍정 확언 일력

 

한 장 한 장 넘겨보니

화려하지 않은 소박함이 느껴지는 그림들이 눈길을 끕니다.

"엄마, 명언이 매일 적혀 있는 줄 알았는데 작가의 말들이네요.

매일 학교 가기 전에 읽으면 좋을 것 같아요."

'글'읽는 걸 좋아하고 '글'의 힘을 알고 있는 아이라

작가가 써준 짧은 글들에서 긍정의 힘을 느끼나 봅니다.

이 여백에 아이가 또 어떤 글들을 써 내려갈지 내심 기대도 해봅니다.

 

6월이 끝나면 7월부터는 뒤집에서 반대쪽을 펴는 거예요.

따로 요일이 표시되어 있지 않아서 2023년만 볼 수 있는 일력도 아니고요.

좋은 말 한마디 한마디가 쌓여 나를 계발시키고

나를 변화시킬 수 있다고 생각해요.

수년 전에 "칭찬은 고래도 춤추게 한다."라는 제목의 책이 있었는데

누구보다 소중한 스스로에게 매일 '좋은 말', '칭찬' 한마디를 해준다면

정말 좋겠죠?

"그동안 내가 좀 불친절했지.

이제 너를 평가하는 건 그만할 거야.

너를 다시 사랑하려 해. JANUARY 2"

"두려움은 실재가 아니다.

내가 품지 않는다면 나를 지나쳐 사라질 것이다. MARCH.6"

"오늘 삶이 내게 허락한 모든 것에 감사한다. AUGUST 23"

"내가 행복한 사람이 될 때

새로운 좋은 사람들이 내 삶으로 들어온다. DECEMBER 12"

매일 '오늘' 나에게 선물하는 '루이스 헤이'의 가장 좋은 한마디.

그 말에 힘을 얻고, 위로를 받기를 바라봅니다.

그렇게 한 번 더, 하루 더 나를 위로하고 사랑하는 날들이 되기를 바랍니다.

<리뷰어스클럽으로부터 제품을 제공받아 쓴 리뷰입니다>

#자기계발 #루이스헤이의365일긍정확언일력 #센시오 #가장좋은한마디

#선물한마디 #루이스헤이 #하루를시작하는말