-

-
숨마쿰라우데 수학 기본서 수학 2 (2026년 고3용) - 2015 개정 교육과정 ㅣ 고등 숨마 수학 (2026년)
권오재 외 지음 / 이룸이앤비 / 2018년 10월
평점 :




고등수학...개념을 잘 알아야 개념을 확장하면서
연계된 개념들이 들어있는 문제를 풀 수 있어요.
수능수학은 개념과 개념간의 연결...
그리고 확장된 개념을 토대로 문제가 나오기 때문에
중등 때 보다 더 개념을 확실하게 알아야
수학을 잘할 수 있어요.
그래서 처음 고등수학을 공부하는 학생들은
개념을 잘 공부해야하는데요.

수학기본서로 고등 수학2의 개념이 잘 나와 있는
숨마쿰라우데 수학2로 공부합니다.
개념학습과 소단원에서 공부한 개념을
바로 확인할 수 있는 Example문제등을
풀면서 기본 개념을 익히구요.
기본예제와 발전예제를 통해서
개념을 심화해 나갈 수 있어요.

중단원별 문제를 풀고 심화 연계학습으로
상위 단계와 연계된 내용을 학습할 수 있구요.
내신 모의고사 테스트가 있어서
수능 수학 유형을 분석해볼 수 있네요.
수학 2 목차를 보면
함수의 극한과 연속이 나오구요.

다항함수의 미분법과
다항함수의 적분법이 나와요.
미분 적분을 공부하는 법
미분과 적분은 서로 연관성이 높죠.

하나의 함수를 보더라도 미분으로 바라보는 동시에
적분으로 바라보는 시각을 키우면서 공부하는 것도 중요하죠.
미분은 접선의 기울기로
정적분은 넓이를 의미하는데
대수적 문제를 가장하고서 기하적 의미를
적용하는 문제들도 수능 수학에 많이 출제되기에
기하에 대한 이해도 있어야 합니다.
함수의 극한과 연속 단원에서는
고등수학(하)에 나오는 함수를 잘 알아야하구요.

다항항수의 미분법과 적분법에서는
고등 수학 상, 하에 나오는 방정식과 함수를
잘 알아야 함수의 개형을 그리면서
문제를 수월하게 풀 수 있어요.
원리를 알고나면 문제로 확인해서
확실하게 그 개념을 알 수 있도록 정리하는 것도 중요합니다.
해설집을 활용해서 이 문제에 필요한 이론이나
어떠한 것을 활용해서 문제를 정확하게 풀 수 있는지를
다시한번 정리해놓는 것도 중요합니다.
문제에 제시된 조건이나 상황을 표시해보고
어떻게 해법으로 연결되는지 체크해보는 것도
문제를 분석하는 중요한 방법이네요.
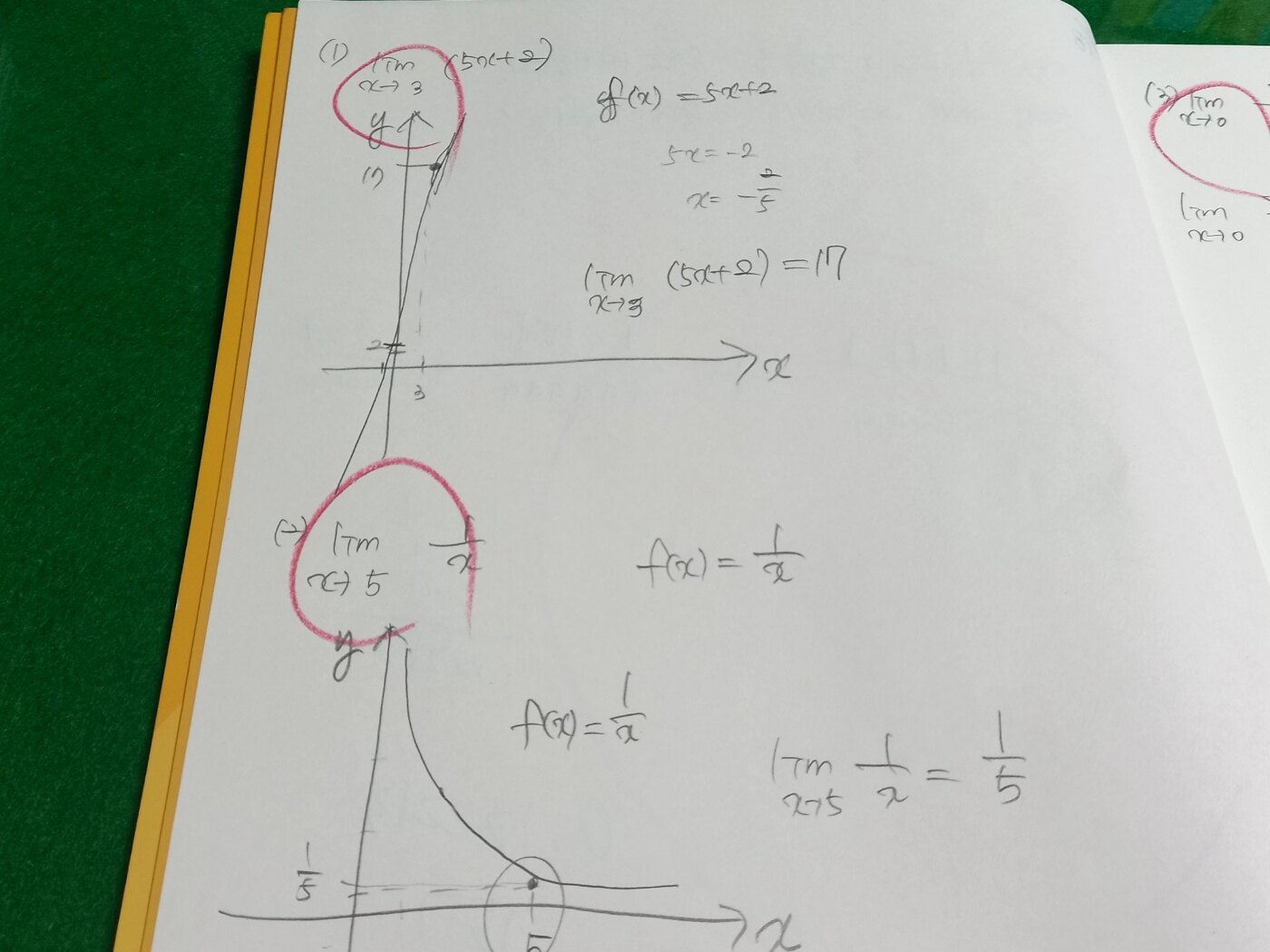
함수의 극한에 대한 개념을 알아보고
예제를 풀어보았습니다.

함수의 그래프를 이용하여 극한을 조사하는
부분이라 함수의 개형을 잘 그려서
극한값을 알아봅니다.
만일 학습하다가 익숙하지 않은 함수가
나온다면 다시 고등수학 상, 하로 가서
함수에 대해서 다시 공부해보는 것도
필요할 것 같습니다.
리뷰퀴즈로 개념을 정리하고
연습문제 A,B로 내용을 확실하게
정리해봅니다. ㅎㅎ
고등수학 기본서로 개념이 교과서처럼
자세히 설명이 되어 있고 문제도 다양하게
나와 있어서 처음 보는 개념서로도
수학 2를 잘 풀어볼 수 있는 수학문제집이네요.
함수의 그래프를 그려서
극한 값을 잘 알아봤어요.

직접 문제를 풀어보면서 확인해가면서
개념을 훑어가는 것도 중요합니다.
확실하게 개념을 학습하고 원리를 알 수 있는
고등수학문제집이라 함수의 극한부터
미적분 까지 개념을 확실하게
익힐 수 있을 것 같네요. ㅎㅎ