수학좀 한다면 최상위수학

최상위 초등 수학 6-2 (2016년용) ㅣ 초등 최상위 수학 (2016년)
궁재범.김명자.천병수 외 지음 / 디딤돌 / 2015년 5월

3% 도전 프로젝트~

와~ 뭔가 대단해 보이지 않나요?

3%라니... 정말?

뭐~ 일단 풀어보죠 뭐~

 

초등 6학년 2학기의 1단원은 쌓기나무예요.

쌓기나무에 대한 심화유형이 8가지로 구성되어 있네요.

 

단원에 들어가기 전 배경지식을 위한

스토리텔링 형식의 이야기로 단원에 대한

관련지식도 습득하고 학습의욕도 높여봅니다.

 

최상위수학의 구성을 한눈에 살펴보자면

바로 이 정도가 되겠군요.

 

1. Math Top

핵심개념과 심화개념, 상위학습 개념 그리고

배경지식도 익힐 수 있으며 Basic Test로

확인도 해봅니다.

 

2. Math Topic

심화 유형문제를 집중 학습할 수 있는데요.

문제해결능력과 사고력을 향상시킬 수 있답니다.

 

STEAM형 유형학습

단원마다 심화유형 마지막에 교과통합유형이

수록되어 있어 융합형 인재를 위한 밑거름을

마련해준답니다.

융합형 인재로의 도약~ 한번 도전해보자구요.
 

3. Level up Test

단원에서 배운 심화개념과 유형을

평가하고 정리해볼 수 있는 단계예요.

 

흠~ 틀리는 문제들이 나타나기 시작하는군요.

뭐~ 틀리는 비율을 보니 그래도 도전해보며 풀어볼

만한 의욕이 꺾이는 정도는 아닌것 같지요?

 

4. High Level

교외 경시대회에서 출제되는 수준높은

문제 단계라고 하는데 아예 풀어보지도 못하고

모른다고 표시한 문제가 6문제 중 2문제나 되네요.

문제 한번 읽어보고 모른다고 포기할 것이 아니라

2번이고 10번이고 읽고 또 읽어보며 풀기위한

다각도의 노력을 해봤으면 하는게 엄마의 바램이기도 하네요.

그렇게 하면서 한문제를 풀어냈을 때의 그 성취감을

느낀다면 도전하는 즐거움도 있는게 바로 수학이니까요.

 

정답지를 보며 스스로 채점~

최상위 팁과 다른풀이도 제공하고 있어서

정답과 풀이보며 또다른 공부가 될것 같아요.

 

특별부록으로 교내경시문제가 단원별 20문항씩

8절 형태로 수록되어 있어요.

 

상위권이 되기 위한 필수문제

사고력을 키우는 고난도 문제

실생활 연계, 교과 통합 문제 수록~

상위권교재 베스트셀러가 그냥 된건 아니겠죠?

수학 좀 한다면 최상위수학~이예요.

엄마표첫종이접기

엄마표 첫 종이접기 - 엄마와 함께 하는 뇌 균형 발달 놀이 교육
뇌 균형 발달 연구회 지음, 이인화 그림 / 로그인 / 2015년 8월

"아~ 못하겠다" 하던 아이가

"내가 했지~ 나도 할수있어~"하며

종이접기에 자신감을 갖게 된 계기!

바로 로그인의 엄마표 첫종이접기가 있어서 가능했어요.

41개월 아이와 종이접기 놀이를 하려면

아무래도 아이보다는 엄마가 다 접어줘야 하는데

이 책은 한번만 접어도 만들기가 되는 수준부터

시작되니 정말 제목 그대로 첫 종이접기책이 맞네요.

생생한 사진 도감식 구성이라는 설명에 맞게

정말 도감을 보는 듯한 생각이 들 정도로

동식물의 생태를 보여주는 사진들이 있구요.

거기에 몇번 접지 않아도 실감나게 할

색종이와 스티커가 들어있답니다.

 

차례부터 그림이 있으니 하나하나 짚어보며

관심을 보이는 4호군이예요.

 

종이접기의 기본기호도 익혀야겠지요?

그러나 너무 쉬워서 그림만 보고도 글을

읽지 못하는 4호군도 이해하는 것 같았어요.

 

뒤에는 스티커와 일반 색종이와는 다른 작품에

사용될 색종이가 들어있어요.

 

먼저 첫페이지를 여니 탄성이 터져나왔어요.

"우와~ 나 수박좋아하는데.... 수박 맛있겠다."

실사가 있으니 더 생생하지요?

수박접기는 1~2번만 접어도 되는 초간단 접기예요.

원형색종이 1장이 필요하지요.

 

원형색종이는 책의 뒤 부록에 있으니 그냥

오려서 사용하면 되겠지요?

 

4호군의 도전~

과연 혼자 접을 수 있을까요?

엄마가 접어주는 걸로 놀이만 즐기는 수준이

아니라 이젠 혼자 접어서 즐길 수 있는 종이접기가 되었답니다.

원래는 절반접고 또 접어 씨를 그려넣으면

끝이지만 밑단을 조금 접어올리니 초록색이

나와서 진짜 수박처럼 되었네요.

 

맛있게 냠냠~ 먹기도 하고....^^

씨도 퉤~ 뱉어내기도 하구요.

 

그 다음은 뛰뛰빵빵 스쿨버스 만들기~

이건 일반 색종이로도 가능해서 집에 있는

색종이를 사용했어요.

엄마표 첫 종이접기에는 아이와 나누기 좋은

대화 주제도 제시되어 있어서 아이와 함께

이야기를 이끌어가기도 좋답니다.

 

네모 색종이를 한번만 네모접기하면 끝~

완전 쉽지요?

거기에 창문과 바퀴 스티커를 붙이면 되니

스티커 붙이는 재미와 조금 더 사실감 있게

완성되는 작품을 보는 재미~ 모두 굿~이예요.

 

다음은 뾰족뾰족 피라미드 만들기예요.

네~ 이번엔 세모접기 두번만 하면 끝이지만

갑자기 4호군은 보드게임으로 즐기던 보물찾기를

가져와서 뭔가를 찾고 있어요.

"피라미드가 어디 있었는데..." 하며 피라미드

그림을 본 기억에 뒤적거리더니 드디어 찾았네요.

바로 이집트였지요.

날마다 보물찾기 하자고 괴롭혀대서 엄마는

진심 피곤했는데 이렇게 또 효과가 나타나는군요.

더 열심히 보물찾기 놀이도 해줘야겠어요. ㅎ

 

세모 꼭지점끼리 맞추느라 초 집중모드~

아직 완벽하게 선을 접어내지는 못하지만

고사리손으로 꾹꾹~ 눌러대는 모습이

귀엽기만 합니다.

 

엄마 눈높이에선 정말 아무것도 아닌데

한두번 접는 시도만으로도 성취감을 느끼게 하니

정말 만족스러운 종이접기 책이네요.

 

아까 만들어두었던 버스를 타고 피라미드를

찾아가는 길~

이렇게 만들기 후 놀이로도 연결되니

좌뇌, 우뇌가 쑥쑥~ 재미도 쑥쑥~

이라는 말에 공감이지요?

 

조류세계에서 살아남기

조류 세계에서 살아남기 1 ㅣ 서바이벌 만화 과학상식 48
곰돌이 co. 글, 한현동 그림, 김성현 감수 / 미래엔아이세움 / 2015년 9월

마블역사상 가장 작고 가장 강한 히어로가 온다~

바로 앤트맨의 이야기이다.

슈트와 헬멧을 착용하고 버튼하나 누르면

개미처럼 작아져 눈에 띄지 않게 적진에 침투해

임무를 완수하는 앤트맨~

그런데 조류세계에서 살아남기에서

특수탐조복을 입고 작아진 지오를 보니

영화를 보는 듯한 착각이 들기도 한다.

물론 앤트맨은 날개가 없긴하지만...

▶ 새들은 어떻게?

조류에 대한 여러가지 정보들로 흥미로웠던

조류세계에서 살아남기~

척추동물 중 하늘을 날 수 있는 동물을 조류~

흔히 새라고 하는데 이 새들은 어떻게 하늘을

날 수 있는것일까?

새가 하늘을 날 수 있는 것은 날개때문이지만

그 외에도 무거운 이빨과 턱뼈대신 가벼운 부리,

오줌을 저장하는 방광도 없고 뼈속도 비어있고

게다가 몸속엔 공기주머니도 있다.

우리가 갖지 못한 날개를 갖고 우리가 다니지 

못하는 하늘을 날기에 동경의 대상이 되기도 하지만

하늘도 우리 생각처럼 낭만적이지만은 않은것 같다.

 

텃새가 아닌 이상 철새들은 계절마다 먼 거리를

이동해야 하니 그다지 쉬운 생은 아니지 않은가~

새에 관한 정보를 보며 마치 새가 된다면?

하는 생각이 먼저 드는걸 보니 요즘 판타지를

너무 많이 봤나보다. ㅎㅎ

 

▶ 매의 눈~

새 중에 매의 눈이 이렇게 좋은지 몰랐다.

우리가 사과나무를 본다면 매는 사과나무

열매에 있는 애벌레를 볼 수 있다니...

인간보다 여덟배까지 시력이 좋다고 하니

정말 '매의 눈'이라고 하는 말이 괜한 말이 아닌것이 신기하다.

 

친절하게 사람눈과 매의 눈 구조까지 대조해주니

조류사전이라 해도 괜찮겠다.

 

▶ 조류세계에서 살아남기

새에 푹 빠져사는 조류박사인 구구박사~

뇌박사는 친구인 구구박사를 위해 하늘을

날면서 새를 관찰할 수 있는 특수탐조복을

개발하고 지오와 케이에게 심부름을 시킨다.

특수탐조복, 새들의 섬, 지오...

왠지 서바이벌 상황과 어울리는 단어들?

새에 대해 공부하며 지오가 빠지게 된 서바이벌

상황까지 흥미진진하게 즐길 수 있는

조류세계에서 살아남기~

과연 지오와 일행은 까마귀와 참매로부터의

봉변에서 어떻게 살아남을지 2권이 기대된다.

스토리텔링 수학 6-2

디딤돌 스토리텔링 수학 초등 6-2 (2017년용) ㅣ 디딤돌 스토리텔링 수학 (2017년)
디딤돌 초등 편집부 엮음 / 디딤돌 / 2015년 5월

아직 초등 시절엔 평소에 공부하는 걸로

시험기간 따로 없이도 상위권 점수를 받고

있어서 시험에 대한 부담감은 조금 덜합니다.

그 비결은 역시 수업시간 집중과 평소

꾸준히 공부하는 것이겠지요?

오늘은 모든 스토리텔링 유형을 다루고 있는

디딤돌 스토리텔링 수학을 소개해볼까 합니다.

 

▶ 스토리텔링 수학의 수준은?

저희는 수학문제집으로 주로 디딤돌 교재를

사용하고 있는데요~

방학동안 가장 쉬운 난이도의 초등수학 원리를

한학기 예습으로 풀고 학기중엔 기본으로

진도를 나가고 있는 중입니다.

거기에 한단원을 마치고 나면 스토리텔링 수학으로

다시 한번 복습을 하곤 하지요.

둘다 중간 난이도의 수준이라 그리 어렵지

않게 마무리 할 수 있는 정도입니다.

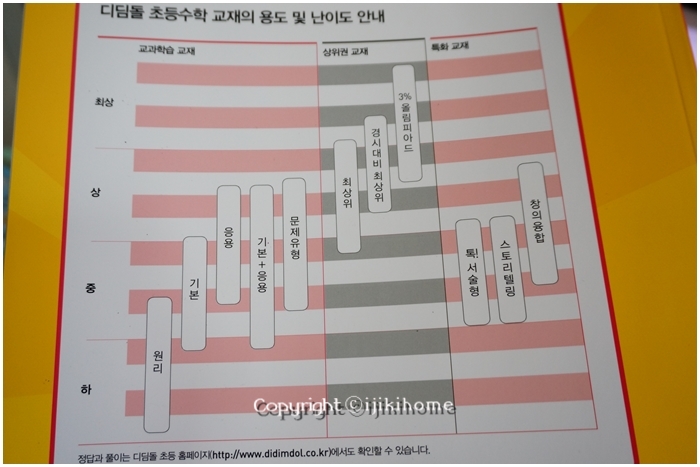
조금 더 수준을 높이고 싶다하시면 아래 표를

보시고 참고하시면 되겠습니다.

학교에선 6학년 2학기 수학 2단원 마무리가

얼마남지 않았다고 하는데 뒤늦게 1단원

마무리로 스토리텔링 수학을 잡았네요.

조만간 2단원 마무리로 다시 스토리텔링수학

2단원을 풀게 생겼어요.

 

그래도 한단원 푸는데 30~40분이면 충분하니

그리 부담스럽지는 않답니다.

 

▶ 스토리텔링 수학의 유형~

문장이 긴 스토리텔링 문제의 해결방법을

배울 수 있다는게 가장 큰 장점인 스토리텔링

수학에는 동화연계형, 실생활연계형, 자료제시형,

교과연계형의 스토리텔링 유형을 만나볼 수 있습니다.

 

▶ 스토리텔링 수학의 해결방법?

긴 문장의 해결방법을 어떻게 익히냐구요?

바로 3단계만 따라하면 되지요.

1 구하려는 것에 밑줄긋기

2 해결단서를 찾아 표시하기

3 찾은 단서로 답 구하기

에이~ 그게 무슨 해결방법이냐구요?

의심스럽다면 일단 한번 따라해보세요.

 

각 문제마다 3단계 학습법을 자꾸 상기시키니

일단 따라서 밑줄도 그어보고 표시도 해봅니다.

그래도 아직 부족한게 문제를 꼼꼼히 읽는거예요.

문제가 길어지면 특히나 더 필요한 부분인것 같아요.

그 이유는 뒤에서 한번 더 이야기해볼께요.

 

▶ 배경지식도 OK~

이 문제는 자료제시형 문제네요.

수학 문제 풀면서 다양한 배경지식들을

접할 수 있어서 수학이라기보다 책을 보는

그런 착각이 들기도 한다지요.

 

2호양이 수학문제 풀다가 "우와~ 진짜 이런게 있어?"

하며 신기해 했거든요.

 

▶ 스토리텔링 수학 실전다지기~

자~ 유형익히기를 마치면 실전다지기가 나옵니다.

 

총 12문제의 실전다지기 문제 속에는

각 해당 유형도 체크가 되어 있지요.

이제 마무리 문제가 다가오네요.

한단원을 다 풀자고 하니 헉~했던 2호양이

막상 풀어보니 그리 많지 않은 양이라

별거아니네~ 하는 반응이었답니다.

 

▶ 정답및 풀이집도 특별해~

문제를 풀었다면 채점도 해야겠지요?

스토리텔링 수학의 정답및 풀이집은 좀 특별해요.

바로 문제집과 같은 구성이거든요.

 

문제집과 똑같은 구성의 해답지~

답 찾기도 편하고 그리고 앞서 말했던

3단계 학습법을 구별하기도 좋답니다.

물론 해설부분도 있는건 당연하구요.

 

▶ 그래도 틀린 이유?

앗~ 아까 이런 건물이 진짜 있느냐며 신기해

하던 문제를 틀렸네요. ㅜㅜ

틀린 이유를 보니 문제를 꼼꼼히 읽지 않은 탓이네요.

맨아래에 1층을 더 만들려고 할때 1층에 놓이게 될

연결큐브가 몇개인지 구하는 문제인데 현재 맨

아래에 있는 큐브의 갯수를 적어놓았어요.

구하려는 것에 밑줄 긋기해야하는 3단계

학습법도 건너뛰고 그냥 풀었군요.

이런 이런~ 맞아요.

읽어야 할 것이 많아지면 대충 대충 읽고

대충 생각해서 푸는 경향이 있는데 다시 한번

기억해야겠어요.

 

긴 문장도 꼼꼼히 읽으며 3단계 학습법으로

이제 스토리텔링 문제 정복하기도 가능하겠지요?

 

▶ 오답봉투로 단원 마무리~

여기서 생각나는것 한가지~

1단원 마무리 복습까지 마치고 나니 방학동안

문제집 풀면서 틀린문제 모아두었던 오답봉투~

 

네~ 그래서 오답봉투에 넣어두었던 1단원

문제를 다시 풀어보았답니다.

총 6문제중에 4문제는 맞췄으니 오답봉투에서

탈출할 수 있는 기회를 주고 또다시 틀린

2문제는 다시 오답봉투로...

 

지금 풀고있는 기본과 스토리텔링 수학의

오답봉투도 만들어서 완벽 단원마무리 해야겠어요.

이제 긴문장의 문제풀이도 문제없다~

스토리텔링 수학이 함께합니다.

내가 나인게 감사하게 되는 책

고양이가 되다 ㅣ 매트 헤이그 걸작선
매트 헤이그 지음, 피트 윌리엄슨 그림 / 미래엔아이세움 / 2015년 7월

부모님의 이혼, 어느날 갑자기 사라진 아빠,

친구들로부터 괴롭힘을 당하고 매사에 소극적인

그래서 더더욱 자기 자신이 싫어졌던 소년 바니~

어느 날 아침 눈을 뜨니 고양이가 되다~

 

"불가능한 일에도 마음을 열어 두어야 진실을

발견할 수 있단다~" - 본문중에서

생일인데도 여전히 아빠에게선 연락이 없다.

개빈 니들은 여전히 바니를 괴롭히고

비상식적인 교장선생님은 주변의 잘못을

모두 바니에게 뒤집어씌우며 잔소리를 한다.

내 아이가 정말로 이런 선생님을 만나면

어쩌나 싶은 아찔한 마음이 들기까지 한다.

세상에는 비상식적인 사람이 너무 많으니까

심지어 선생이라는 탈을 쓴 그 무엇도 있을테니까...

그럴 경우에도 난 끝까지 내 아이를 믿고

응원해 줄 수 있는 엄마인가? 라는 생각이 들었다.

그런 엄마가 되어야 겠다는 생각까지...

힘든 하루를 보낸 바니는 우연히 고양이를 보고

고양이를 부러워한다. 진심으로 고양이가 되고 싶어한다.

그런데 다음날 눈을 뜨니 고양이가 되어 있었다.

그러나 평온해 보이고 아무 걱정없이 살 것 같았던

고양이의 삶도 그리 녹녹치 않다.

죽을 고비를 넘고 넘으며 바니는 비로소

내가 나로 있을 수 있다는 것이 얼마나 행복한지를 깨닫는다.

 

고양이~ 그리고 동물

고양이에겐 신비한 힘이 있다.

고양이는 마법사이다.

고양이가 부릴 수 있는 마법 중 최고는

'사람과 몸을 바꿀 수 있는 능력'???

황당하지만 작가의 상상력은 왠지모를 비밀을

갖고 있는 것 같은 고양이로부터 출발한다.

이 세상 고양이들이 내 삶을 노리고 있다면?

역시나 고양이의 그 눈빛엔 뭔가가 있는 듯하다.

특히나 동물을 학대한 경험이 있다면 조심하시길...

이 책에서 사람과 몸을 바꾼 그 고양이들의 결심도

인간에게 학대받은 경험으로부터 시작되기 때문이다.

내가 나로 있는건 행복한 것~

교장선생님이 바니를 유독 싫어했던 이유가

밝혀지는 순간, 그리고 바니와 몸을 바꾼 고양이의

정체, 사라진 아빠와 공포고양이의 비밀~

이야기속의 치밀한 구성에 감탄하며

마지막 페이지까지 책을 놓지 못하며 읽다가

결국에는 내가 나로 있는 것이 얼마나 행복한지를

느끼며 책장을 덮게 된다.

작가의 귀여운 유머에 미소지으면서...