설민석의 무도 한국사특강

설민석의 무도 한국사 특강 ㅣ 휴먼 특강 2
설민석 지음 / 휴먼큐브 / 2014년 1월

올 9월 영화 암살을 보고 와서 찾아 보게 된

유투브속 암살을 통한 역사이야기를 들려주시던

설민석 선생님의 강의가 참 인상적이어서

그 후로도 역사관련 영화를 보게 되면 꼭 찾아보게 되는데요.

그래서 설민석의 무도 한국사특강이란 책도

보자마자 고민없이 바로 신청하게 되었답니다.

그런데 책을 받고 보니 2014년 1월에 1판

인쇄가 되었던 책이더군요.

이런 책을 왜 이제야 알게 된건지...ㅜㅜ

게다가 무한도전 TV특강에 출연하신 건

2013년 5월 11일 329회~

저 무한도전도 다시보기 했답니다.

설민석 선생님 보기위해서요~ ㅋ

무한도전에서도 인물편과 사건편 문화유산편으로

나뉘어 진행이 되었었는데 설민석 선생님은

인물편에 나오셨었지요.

책을 읽다보면 입체감있는 선생님의 말투가

스테레오로 들려오는 듯 해요.

그만큼 책속에서도 살아숨쉬는 선생님의

음성을 들을 수 있답니다.

 

역사적으로 왕권을 강화하기 위한 왕들을

살펴보면 세가지의 방법안에 있다고 하는데요.

조선시대 태종 이방원처럼 칼을 들어

반대파를 한번에 척결하는 방법과

일본의 도요토미 히데요시처럼 머리를 써서

반대세력을 교묘하게 제거하는 방법,

그리고 고려 태조 왕건처럼 사랑과 덕으로

반대파들을 내편으로 끌어들이는 법이 그것입니다.

도요토미 히데요시는 임진왜란이란 방법으로

반대세력을 교묘히 제거하면서 본인의

힘은 강화할 수 있었지만 그 여파로

희생된 우리민족을 생각하면 마음이 아려옵니다.

 

요즘 육룡이 나르샤를 재미나게 보고 있는터라

이방원이나 이성계 이야기에 더 흥미를 보이게 되는데요.

역사는 그것을 바라보는 시선에 따라

달라보인다는 것도 참 흥미롭지요.

위화도 회군이 혁명이냐 쿠테타냐를 두고도

보는 시선에 따라 판단이 달라지겠지만

육룡이 나르샤 이번주 방송 부분에서

그 위화도 회군 이야기가 그려진터라

더 입체적으로 다가왔습니다.

결론은 이미 알고 있는 역사이야기라도 말이지요.

 

무한도전에서도 타고난 천재 세종과

후천적으로 천재가 될수밖에 없었던 정조이야기도

흥미로웠습니다.

바로 영화 사도에서도 등장했던 영조, 사도세자,

정조로 이어지는 이야기속에서 정조를

이해하고 죽음의 위협속에서 밤에는 잠을

이루지 못했던 정조에 대해 들었기 때문이지요.

이렇게 퍼즐조각들이 맞춰지듯 역사를

이해할 수 있다는 것도 참 재미있습니다.

 

역사속의 인물과 위화도회군, 임진왜란,

3·1운동, 6·25전쟁 등과 같은 사건,

그리고 건축, 예술등의 문화유산에 걸친

역사속 이야기와 그 속에 숨은 이야기까지

역사가 이렇게 재미있는 거였나 싶은 정도로

재미나게 읽을 수 있었습니다.

잃어버린 땅 간도, 잃어서는 안 되는 땅 독도~

우리 것을 지키는 힘이 바로 역사에서

찾을 수 있다는 말씀도 마음에 와닿습니다.

 

역사는 사람들에게 과거를 알려줌으로써

미래를 판단할 수 있게 한다 - 토머스 제퍼슨

미생물에 대해 알려주마

브리태니커 만화 백과 : 미생물 ㅣ 브리태니커 만화 백과 19
봄봄 스토리 글, 김덕영 그림, 신동훈 외 감수 / 미래엔아이세움 / 2015년 11월

미국 시카고의 엔사이클로피디어 브리태니커사의

브리태니커 러닝 라이브러리를 바탕으로

초등학생이 꼭 알아야 하는 교과내용을

체계적으로 구성한 만화백과가 나왔다.

지식의 10가지 갈래를 내용 분류의 기준으로 삼아

총 50권으로 출간될 브리태니커 만화백과 중

10권이 1차 출간을 마쳤다.

빛과 소리, 미생물, 날씨, 지구, 곤충과 거미,

물질과 변화, 양서류와 파충류, 힘과 에너지,

갯벌, 우주가 그 10권에 해당된다.

오늘 읽어본 책은 눈에 보이지는 않지만

알수록 놀라운 미생물에 대한 책이다.

 

시각적 이미지가 많은 덕분에 흥미유발은 물론

비주얼 만으로도 이해가 쉬워진다.

그렇다고 비주얼만으로 끝이 아니니 걱정없다.

정보페이지는 물론 심화학습까지 가능한

백과사전이니 말이다.

 

사람들이 미생물을 처음 발견한 건 언제였을까?

눈에 보이지 않는 미생물이기에 그것을

눈으로 확인할 수 있는 현미경이 발명되고서 부터이다.

현미경은 1608년 네덜란드의 안경제작자인

자카리아스 얀센이 발명한 것으로 우연히

두 개의 렌즈를 겹치면 사물이 크게 보인다는

사실을 발견하고, 이 원리를 이용해

현미경을 만들었다고 한다.

 

식물처럼 광합성을 하지 않고, 동물처럼

스스로 영양분을 구할수도 없어 주로

다른 생물에 붙어사는 버섯이나 곰팡이,

효모같은 미생물을 진균류라고 한다.

이런 진균류는 해로운 것도 많지만

이로운 진균류도 있다는 사실~

바로 미생물로 미생물을 잡는 항생제

페니실린이 대표적인 것이다.

푸른곰팡이가 포도상 구균의 세포벽 합성을

방해하여 죽게 하는 원리를 이용한

페니실린으로 현대의학이 본격적으로

발달하면서 인류의 수명도 크게 늘었다.

 

빵반죽을 부풀리는데도 진균류의 힘이

필요한데 바로 포도나 사과처럼 달콤한

과일에 붙어사는 미생물 효모가 그것이다.

효모는 빵이나 맥주를 발효시키는데 꼭

필요한 진균류이다.

여기서 발효란 미생물이 유기물을 분해해서

알코올이나 이산화탄소등을 생기게 하는 과정이다.

유기물을 분해한다는 점은 부패와 비슷하지만

이로운 물질을 만들어내면 발효,

해로운 물질을 만들어내면 부패라고 한다.

 

겨울이 시작되기 전 가장 큰 일거리인

김장을 앞두고 있는 요즘~

바로 이 김치도 우리나라의 대표적인

전통 발효식품 중 하나이다.

배추를 소금물에 절여 해로운 세균을 없애고

김치 내부조차 호기성 세균으로 인해

산소가 살 수 없는 환경이 되는데

이런 환경때문에 젖산균이 살아남는다.

젖산균은 장 건강은 물론 면역력도 높여주고

배변활동 뿐 아니라 알레르기, 충치, 비만,

노화 억제와 간 보호까지 돕는 고마운

세균이란 말씀~

이렇게 보니 미생물도 참 고맙게 여겨진다.

 

김치 외에도 젖산균은 요구르트, 치즈등에서도

얻을 수 있다.

그렇다면 요구르트와 치즈를 한번 만들어볼까?

직접 만들어볼 수 있는 활동으로 발효에 대해

젖산균에 대해 확실히 이해할 수 있겠다.

 

미생물이 무엇인지부터 시작해서

여러가지 미생물의 종류와 인간과 미생물의

관계, 그리고 미생물의 쓰임새까지 알아본

브리태니커 만화백과 미생물~

뒷장에서 만나는 브리태니커 세계 대박과사전으로

읽는 미생물로 심화학습까지도 가능한

브리태니커 만화백과이다.

 

언제봐도 신비로운 우주

브리태니커 만화 백과 : 우주 ㅣ 브리태니커 만화 백과 1
봄봄 스토리 글, 이정태 그림, 한국초등과학교육학회 외 감수 / 미래엔아이세움 / 2015년 11월

학창시절엔 참 어렵게만 느껴졌던 것들이

그 시절의 몇배의 나이를 먹고난 후 보니

새삼 이렇게 재미있는거였나? 싶다.

그만큼 생각의 깊이와 폭이 넓어진 덕분일까?

같은 책을 읽어도 읽는 이에 따라 깨달음과

감동이 달라지는건 어쩔 수 없지만 아이들도

도전과 감동이 남달랐으면 좋겠다는 생각을 해본다.

 

호기심과 관찰력 덕분에 아무런 장비도 없던

시절 지구의 모양을 궁금해하고 뛰어난

관찰력으로 사실을 밝혀냈던 사람들~

그 호기심과 관찰력은 지금도 진행형~이렸다.

옛날에 비해 과학적으로 밝혀진 사실도 많지만

그럼에도 여전히 밝혀지지 않은 것들이 많으니 말이다.

 

지구가 평평하다고 굳게 믿었던 시절~

그러나 지구가 둥글다는 것을 알았을때 사람들은

어떤 생각이 들었을까?

지금 우리가 굳게 믿고 있는 것들조차

사실은 뒤바뀌어야 할 것들은 또 얼마나 있을까?

그렇기에 내가 알고 있는게 다가 아니라는

생각에 밝혀진 것들조차 의심하게 되기도 한다.

 

지구의 자전과 공전, 낮과 밤이 생기는 이유~

 

그리고 지구뿐 아니라 행성별 자전축도 신기하다.

참, 여기서 행성이란?

태양처럼 스스로 빛을 내는 천체는 항성

반면, 스스로 빛을 내지 못하고 항성의 주위를

도는 천체는 행성이라고 한다.

또 지구 주위를 도는 달처럼 행성의 주위를

도는 천체는 위성이라 부른다.

 

태양의 행성인 수성, 금성, 지구, 화성,

목성, 토성, 천왕성, 해왕성의 여덟개가

태양 주위를 공전하고 있다.

내가 학창시절에 배울땐 여기에 명왕성까지

포함되었었는데 지금 명왕성은 행성의

자격을 잃었다.

그 이야기는 뒤에서 다시 하기로 하고...

여덟개의 행성은 지구형 행성과

목성형행성으로 나뉘는데 먼저 수, 금, 지, 화는

지구와 성격이 비슷한 행성으로 지구형행성이라 불린다.

지구형 행성은 단단한 땅을 가지고 있고

위성의 수가 적거나 없기도 하다.

 

반면 단단한 땅이 없는 기체덩어리 행성도

있으니 바로 목성형 행성인 목성, 토성,

천왕성, 해왕성이다.

 

그리고 원래 태양계의 아홉번째 행성이었다가

2006년 행성의 자격을 잃은 명왕성이야기~

명왕성보다 더 큰 '에리스'같은 천체들이

추가로 발견되면서 혼란에 빠진 과학자들은

2006년 세계의 천문학자들이 모여 회의를 했다.

결과적으로 행성의 새로운 기준을 정하고

명왕성은 '134340 플루토'로 이름을 바꾸고

'왜행성'이라는 새분류에 속하게 되었다.

명왕성은 행성의 3가지 기준 중 세번째 기준을

만족하지 못하는데 명왕성의 위성인 카론은

일반적인 위성과 달리 크기가 명왕성과 비슷하고

카론이 명왕성을 도는 것이 아니라 서로

바라보며 돌고 있다는 사실이 밝혀졌기 때문이다.

 

지구형 행성과 목성형 행성~ 헷갈리다고?

브리태니커 만화백과는 이렇게 그림으로

사진으로 표로 정리가 잘 되어 있어서

마지막 이해까지 깔끔하게 돕는다.

 

태양계와 별, 그리고 우주를 향한 도전까지

이어지는 브리태니커 만화백과 우주 편~

심화학습도 가능하니 더 만족스러운

브리태니커 만화백과다.

진짜 앎의 재미를 주는 책~

브리태니커 만화 백과 : 양서류와 파충류 ㅣ 브리태니커 만화 백과 9
봄봄 스토리 글, 최우빈 그림, 한국초등과학교육학회 외 감수 / 미래엔아이세움 / 2015년 11월

그저 흔한 백과사전의 한 종류려니 했다.

백과사전의 지존이라 불리는 브리태니커사의

'지식의 10가지 갈래' 체계를 기준 삼아

모든 영역에 관한 지식을 균형있게 만들어낸

것이라고 해도 그저 백과사전이려니 했다.

초등학생 수준에 맞춘 브리태니커 만화백과~

그런데 양서류와 파충류를 읽다보니 어? 하게 된다.

관심분야도 아니거니와 그저 징그럽기만 한

양서류나 파충류 뭐~ 그런 지식 정보들이,

아니 그럴거라 여겼던 분야를 이렇게 재미있게 엮어놓다니...

 

▶ 인포그래픽~

책의 첫머리의 인포그래픽에는 책 한권의

핵심 내용이 들어있다.

양서류의 한자 뜻이 '두 곳에 사는 무리'라는

뜻으로 물과, 육지를 오가며 사는 무리란다.

양서류의 특징, 도롱뇽, 무족영원, 개구리vs두꺼비~

그리고 뒷장엔 파충류에 대한 인포그래픽도 있다.

책을 읽기 전 살펴본 첫장의 인포그래픽은

책을 다 읽고 난 후 한번 더 살펴보니

더 쉽게 이해가 된다.

 

▶ 양서류~

양서류를 좋아하는 로운이가 우리나라

최고의 생물박사인 아버지를 둔 친구 슬기

덕분에 다큐멘터리 촬영에 따라가게 되면서

이야기가 시작된다.

양서류는 개구리처럼 물속과 땅위에서 사는 동물~

파충류는 뱀이나 도마뱀 같은 동물로

양서류와 달리 주로 땅위에서 사는 동물~

정도로만 구분하던 로운이도 이번 다큐

촬영을 통해 많은 것을 배우게 된다.

새끼인 올챙이가 개구리가 된 후보다 더

큰 패러독스 개구리나 부화 과정이 특이한

피파개구리 같은 특별한 개구리들 이야기도 흥미롭다.

 

들어도 들어도 여전히 헷갈리기만 한

개구리와 두꺼비의 구분~

이번 기회에 확실하게 구분해보자.

 

지금까지 배운 내용을 그림으로 정리해 둔 로운이~

이렇게 정리하니 정말 이해가 쏙쏙된다.

양서류 중 발이 없는 특이한 종류인 무족영원~

무족영원은 몸통이 길고 다리가 없는 것이

지렁이랑 비슷하지만 뼈가 없는 지렁이와

다르게 머리뼈와 척추를 가지고 있다고 한다.

영원이나 도롱뇽은 무족영원과 다르게

네개의 다리를 가지고 있고 다 자란뒤에도

꼬리를 가지고 있는게 특징이다.

물속에서만 사는 도롱뇽 우파루파도 있는데

우파루파는 멕시코에 사는 도롱뇽의 한 종류이다.

원래 이름은 '아홀로틀'로 '물속에서 노는 개'

라는 뜻을 가지고 있다.

이름처럼 평생을 물속에서 지내기 때문에

다 자란 후에도 어린 도롱뇽이 가지고 있는

깃털 모양의 겉아가미를 가지고 있다.

 

▶ 파충류~

그렇다면 파충류에 대해서도 알아볼까?

파충류는 '기어 다니는 동물'이란 뜻이다.

몸이 비늘이나 등딱지로 덮여있고 주변의

온도에 따라 체온이 달라지는 특징이 있다.

폐로 호흡하고 피부의 비늘이 몸속 수분이

빠져나가지 않게 막아줘서, 양서류와 달리

사막과 같은 건조한 지역에서도 살 수 있다.

대부분의 파충류는 네개의 다리를 가지고 있지만

뱀처럼 다리가 없는 종도 있다.

 

도마뱀과 이구아나, 도롱뇽을 세쌍둥이처럼

닮았다고 생각했던 슬기~

그러나 도마뱀과 이구아나는 파충류,

도롱뇽은 양서류로 구분된다.

얼핏 보기엔 비슷해 보이지만 피부부터

다르고 생김새도 다르다고 하니 이번 기회에

확실히 구분해두자.

 

뱀들의 천국 코스타리카에 간 다큐 촬영팀~

중앙아메리카 남부에 있는 작은 나라

코스타리카에는 지구에서 가장 많은 종류의

뱀이 서식하는 곳으로 유명하다는데 이곳에

사는 뱀의 종류만도 무려 130여종~

이중에는 사람에게 아주 위험한 독을 가진 독사들도 있다.

 

▶ 양서류와 파충류~

여기서 다시 정리해보는 양서류와 파충류의 차이점~ (p158)

	양서류	파충류
숨쉬기	피부호흡, 폐호흡	폐호흡
피부	매끈하고 촉촉한 피부	단단하고 건조한 비늘이 덮인 피부
사는 곳	물과 땅을 오가며 물가나 주로 습한 곳에서 산다.	열대지방에서부터 사막지역까지 다양한 지역에 분포되어 있다.
새끼	변태의 과정을 거쳐 유생과 성체의 생김새가 다르다.	변태하지 않아 새끼와 어미의 생김새가 같다.

환경에 적응하며 살아가는 양서류와 파충류~

그런 양서류와 파충류가 환경오염과

사람들의 마구잡이 사냥으로 멸종위기에

처한 동물들도 늘어나고 있다고 하니

다시 한번 돌아봐야할 문제가 아닐 수 없다.

더 자세히 알고 싶은 내용을 간추려놓은

브리태니커 세계 대백과사전으로 읽는

양서류와 파충류에 대한 심화내용도 책

후반부에 있으니 깊이 있는 지식정보까지

모두 섭취해야겠다.

정다면체 만들기 그리고 큐브

내일은 수학왕 10 - 입체도형의 성질 ㅣ 본격 스토리텔링 수학 만화 10
곰돌이 co. 글, 박강호 그림, 이경희 감수 / 미래엔아이세움 / 2015년 10월

수학왕 캠프의 우승이 달린 마지막 대결~

그 대결상대는 다름아닌 제1회 수학왕 캠프

수상자들로 구성된 골든팀~

강무한이 속한 8반을 제외한 모든 반이

골든팀과의 대결에서 패배한 가운데

모든 눈과 귀가 8반에게 집중됩니다.

 

골든팀과 8반의 대결주제인 입체도형은

5, 6학년 수학교과와도 연계된 주제인데요.

2양의 지난 중간고사 범위이기도 했기에

이번 주제 입체도형은 왠지 친근하게 느껴지기도 합니다.

특히나 강무한의 입체도형에 대한 접근방식에

대해 알고 나면 이제 더이상 입체도형이 낯설게

느껴지진 않을것 같습니다.

 

▶ 플라톤의 입체 vs 공간도형

수학왕 캠프의 우승자들로 구성된 골든팀은

역시나 브레인답게 플라톤의 입체를 이용해

입체도형을 완성한 모습입니다.

반면 8반의 입체도형은 왠지 친근해 보이지요?

 

그렇다면 골든반이 이용한 플라톤의 입체란?

바로 정다면체 다섯종류로 우주의 기본요소를

설명한 것입니다.

정삼각형으로 만들 수 있는 정다면체는

정사면체, 정팔면체, 정십이면체~

그리고 정사각형으로는 정육면체~

정오각형으로는 정십이면체를 만들 수 있는 것이지요.

반면 8반이 만들어낸 공간도형은 우주의

기본요소?같은 거창함은 없지만 이미 우리가

만지고 보아왔던 일상생활속에서의

입체도형이기에 수학을 바라보는 시각을 넓혀주었지요.

개정된 수학의 목표이기도 하구요.

참~ 강무한이 만들어내었던 종이컵을 이용한

구 만들기가 다시 자세히 설명되어 있네요.

종이컵은 아래로 갈수록 좁아지는 모양이므로

옆면을 이어붙이면 중심이 안쪽으로 모이게 되고

입체인 종이컵의 위, 아래, 옆 방향으로 계속 붙이다보면

속이 빈 구의 형태가 만들어진다는 것인데요.

이런 기발한 생각 자체가 참 신기하기만 합니다.

이건 꼭 직접 만들어봐야겠습니다.

 

▶ 27개의 정육면체~ 큐브~

참 이번 책에서는 비몽사몽중에도 큐브를

맞추던 수학천재 함수영의 모습이 보이기도 했는데요.

큐브는 정사각형 모양의 면 6개로 둘러싸인 도형

정육면체가 27개 모여 큰 정육면체를 이룬것이지요.

이런 큐브를 맞추는 방법엔 규칙이 있는데

이 규칙을 외워 반복해서 연습하면 맞출 수 있다지요.

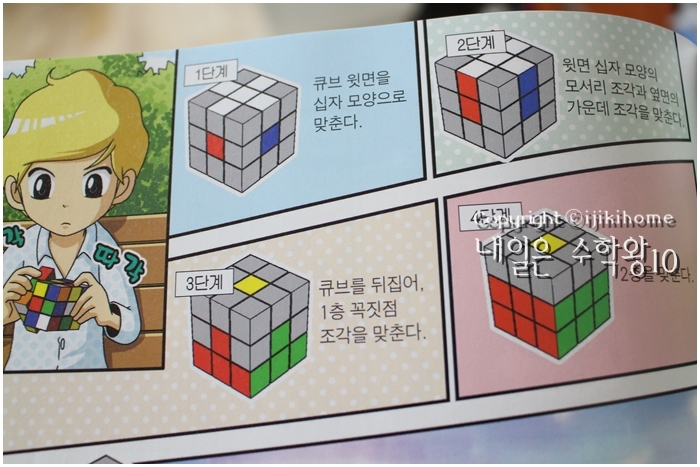
그런데 큐브를 통해서 깨달은 사실 하나,

큐브를 처음 맞출때는 무조건 한면을 먼저

맞추려고 하면서 처음 맞춰놓은 면에 집착할수록

이미 맞춰놓은 면까지 엉망이 되어가는

큐브를 볼 수 있는데요.

전체를 완성하기 위해서는 작은 부분에 집착

하면 안 된다는 깨달음을 통해 수학천재 함수영의

앞으로의 계획이 세워지는 것 같습니다.

그렇다면 큐브 맞추는 방법, 아니 큐브맞추는

공식 한번 알아보고 갈까요?

http://ijikihome.blog.me/220165266073

 

 

▶ 내일은 수학왕 체험키트

이번 내일은 수학왕10의 체험키트는

전개도를 접어 만드는 신비한 정다면체입니다.

입체도형을 구성하는 면, 모서리, 꼭짓점을 알고

입체도형의 전개도를 이해할 수 있지요.

전개도는 이미 준비되어 있으니 선대로

접어 붙이기만 하면 된다는 사실~

참~ 쉽죠 잉~^^

빨간색 정육면체 종이 전개도의 접는 선을

따라 접어 정육면체 모양을 만듭니다.

초록색 띠가 있는 정십이면체 전개도를 접어

정십이면체 모양을 만드는데요.

이때 앞에서 만든 정육면체의 모서리와

정십이면체의 면이 만나도록 정육면체를

넣고 정십이면체를 완성합니다.

파란색 띠가 있는 정이십면체 전개도를 접어

완성하기 전 앞에서 만들었던 정십이면체의

꼭짓점이 정이십면체 면의 중심과 만나도록

넣고 정이십면체를 완성합니다.

노란색 띠가 있는 정팔면체 전개도를 접어

완성하기 전 정이십면체의 면이 정팔면체의

면과 만나도록 넣고 정팔면체를 완성하구요.

보라색 띠가 있는 정사면체 전개도를 접어

완성하면서 안에 정팔면체의 꼭짓점과

정사면체 모서리의 중점이 만나도록 넣어

완성합니다.

마지막으로 빨간색 띠가 있는 정육면체

전개도를 접어 완성하면서 정사면체의

모서리가 정육면체 면과 맞닿게 넣어

완성하면 된답니다.

완성된 정다면체를 통해 끝없이 순환하는

정육면체, 정사면체, 정팔면체, 정이십면체,

정십이면체의 관계를 생각해 볼 수 있습니다.

체험키트뿐 아니라 체험활동지도 있으니

정리하며 오일러의 다면체 정리도 알아볼 수 있답니다.

체험키트를 통해서 그리고 강무한의 입체도형을

바라보는 시각을 통해서 우리 주변에 널린

많은 입체도형들의 핵심원리도 알아볼 수 있었던

재미난 시간이었습니다.

수학이 이렇게 재미있을 수도 있네요.