
Math on Trial: How Numbers Get Used and Abused in the Courtroom
by Leila Schneps, Coralie Colmez (Basic Books 2013.3.)
우리 말로 하면 <법정에 선 수학>이라고 할까, 재판에서 수학이 증거로 사용된 사례에서 수학이 어떻게 오용되었는가 하는 이야기를 들려 주는 책이다.
사법과 수학이라니 평소에 만날 일이 별로 없을 것 같은 어울리지 않는 짝이다. 그런데 뭔가 싶어 별 기대 없이 펼쳐본 책이 빨려들 정도로 재미 있었다. (아무래도 알 수 없는 수학이지만 나의 삶과는 큰 관련이 없을 것 같아 안심하고 있었는데 그게 일상에 파고들어 파괴적인 위력을 발휘하고 있으니 웬만한 스릴러 저리 가라;;; 옛날에는 성직자들만 성서를 읽고 해석할 수 있어서 거기에서 무한권위가 나왔다던데 오늘날에는 수학을 몰라서 억울한 꼴을 당할 수도 있는 건가!)
주로 사용된 수학은 일상생활과 관련이 많은 확률과 통계다. 수학교과서 가장 뒤쪽에 실려 있어 국민적으로 경시되지만 (내가 수능 볼 때는 확률과 통계가 아예 시험 범위에 없었다. 사과벌레씨한테 어제 들었는데 집합이 수학교과서 가장 앞에 나오는 것이 우선순위상 적당하지 않다고 하여 개정 교과서에서는 뒤로 밀렸다고 한다. 이참에 확률통계를 1장으로?) 직관적 세계와 밀접한 관련이 있는 분야. 그런데 이 책을 읽으면서 확률과 통계에 대해 우리가 직관적으로 생각하는 것과 수학적 결과는 다른 경우들을 보고 깜짝 놀랐다.
이 책에 실린 영국, 미국, 이탈리아, 네덜란드 등 여러 나라에서 있었던 열 가지 사건 가운데에는 몇 년 전 세계적으로 떠들썩했고 아직도 재판 중인 어맨더 녹스 사건, 폰지 사기의 원조 찰스 폰지 사건, 19세기로 거슬러 올라가 전설적인 수전노 헤티 그린의 유언장 위조 사건, 드레퓌스 사건(지문 감별법 이전에 범죄자 식별 시스템으로 널리 쓰였던 베르티용 시스템의 베르티용 씨가 부정확한 증언으로 드레퓌스의 유죄 판결을 유도했다는 사실을 이 책에서 알게 되었다)처럼 잘 알려진 사건도 있고, 나머지 사건들도 증거가 부족해 판결을 내리기 어려운 상황에서 '수학'이 결정적 역할을 했다는 점에서 법률사적으로 중대한 사건들이다. 현대에 해당하는 앞부분은 답답한 사법 시스템, 억울한 누명, 편견에 물든 수학이 등장하는 재판 과정 이야기가 지금 겪는 것처럼 생생했는데, 폰지-헤티 그린-드레퓌스가 나오는 뒤쪽 이야기는 (흥미로운 이야기이기는 하나) 옛날 이야기 같아서 역사책 읽듯 조금 다른 기분으로 읽었다.
사건의 발단과 전개, 결과를 세세히 전달하여 법정 드라마처럼 흥미진진하게 펼치지만 사건의 진상을 밝히는 책은 아니다. 단지 재판에 쓰인 수학이 잘못되었기 때문에 그에 따라 내려진 판결은 정당하지 않다는 것을 입증할 뿐이다. 나중에 다른 의학적 증거나 증언 들이 추가되면서 진상이 좀 더 명확해진 사건도 있지만, 몇몇 사건에서는 수학적 증거 때문에 유죄 혹은 무죄 판결을 받은 사람이 실제 범인인지 아닌지, 곧 판결 자체가 결과적으로 옳았는지 옳지 않았는지에 대해서 말할 수는 없고 단지 과정이 잘못되었다는 것을 지적하고 정확한 계산을 보여준다. (그렇기 때문에 좀 맥 빠지는 감은 어쩔 수가 없다.) 결론이 나온 사건도 물론 있다. 소아병동 간호사였다가 환아들을 무더기 살해한 혐의로 기소된 루시아 데 베르크 사건(7장)에서는 재판이 잘못되었다는 것을 알아차린 사람들이 수년에 거친 조사와 재계산 끝에 판결을 반박하는 연구서를 발표했고 그 덕분에 무죄판결을 받게 되어 '수학적 정의'가 실현되기도 했다(재판이 끝나기까지 데 베르크가 이미 수년 복역했고 그 와중에 뇌졸중을 일으켰으니 해피엔딩이라고 할 수 있을지는 모르겠다).
책 중에서 다이애너 실베스터 사건(5장)을 조금 옮겨 본다.
1972년에 다이애나 실베스터라는 여자가 강간 살해 당한 채로 발견된다. 피해자의 몸에서 정액의 흔적이 발견되었으나 당시에는 DNA 감식법이 없었기 때문에 범인을 찾을 수 없었고 결국 미해결로 남았다. 2003년에 샌프란시스코 경찰은 과거의 미제 사건을 DNA 감식이라는 새로운 기술로 해결해 보기로 한다. 30년 전에 보관해 두었던 다이애너 실베스터 살인범의 정액 샘플이 있었던 것이다. 그런데 샘플이 변질되어, 변별에 사용하는 13쌍의 유전자좌 가운데 다섯 쌍을 확인하고 다른 두어 쌍에서는 일부만을 확인할 수 있었다. 아무튼 이 DNA 프로필과 일치하는 DNA를 가진 72세의 존 퍼킷 노인을 체포한다. (존 퍼킷은 성폭행 전과가 있으며, 나이, 당시 거주 지역, 당시 목격자의 증언 등과 외양도 일치했다.)
그런데 재판 중 변호인측에서 FBI가 사용하는 RMP(랜덤 매치 확률. 증거물과 임의의 사람의 DNA 프로필이 일치할 확률)에 의문을 제기한다.
일단 유전자좌 일치 확률을 대략적으로 한번 계산해 보자. 13쌍의 유전자좌 각각이 특정 위치에 나타날 확률은, 통계적으로 밝혀진 바에 따르면 유전자마다 조금씩 다르기는 하나 평균적으로 1/13(약 0.075) 정도 된다고 한다. 유전자좌 각각은 서로 독립적 요인으로 알려져 있으므로, N개의 유전자좌가 일치할 확률은 0.075의 N승이다. 따라서 9개 유전자좌가 일치할 확률은 POWER(0.075,9)이다. 계산해 보면, 9개 일치 RMP가 130억분의 1로 명시되어 있는데 이것과 아주 비슷한 수치가 나온다.
그런데 문제는, 변호인 측에서 최근 연구 결과를 들어 RMP의 신빙성을 문제 삼은 것이다. 트로이어라는 연구자가 2001년 DNA 데이터베이스를 가지고 조사한 바에 따르면, 65000명의 DNA 가운데에서 혈연관계가 없는데 9개 유전자좌가 일치하는 경우를 122쌍, 10개가 일치하는 경우를 10쌍이나 발견한 것이다.
65000명 가운데 122쌍이라는 결과는 130억분의 1의 확률이라는 RMP와 차이가 나도 너무 많이 난다. 직관적으로 생각하기에 둘 중 하나는 잘못된 것일 수밖에 없었다. 어떻게 이런 일이 일어났고 둘 중에 어떤 게 옳은 것일까?
결론부터 말하자면 두 가지 다 옳을 수 있고 모순을 일으키지 않는다.
왜 그런가 하면, 우선 13개 유전자좌 중에서 9개를 뽑는 경우의 수는 715개이다. (13C5)
또, N명을 가지고 만들 수 있는 커플의 수는
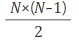
이므로, 65000명이 만들 수 있는 커플의 수에, 9개 유전자 추출 경우의 수 715를 곱한 것이 서로 일치하는지 검증할 샘플의 개수가 된다. 계산해 보니
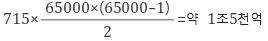
이나 된다.
시료 개수 1조5천억에 일치 확률 130억분의 1을 곱하면 116이 나온다. 데이터베이스 연구에서 발견된 122쌍하고 큰 차이가 없는 수치다!
이건 사실 생일 문제라고 하는 어디에선가 한두 번은 들어 봤을 패러독스다. 사람이 임의로 모였을 때 생일이 같은 두 사람이 있을 확률과 특정한 사람과 생일이 같은 사람이 있을 확률을 계산해 보았을 때 얼핏 비슷해 보이는 두 가지 경우의 확률이 크게 다른 것과 마찬가지다. 그리고 이 두 가지 모두 존 퍼킷이 유/무죄일 확률은 아니다. (이 확률 계산은 뒤에 자세히 이어진다.)
이 책에서는 엄밀하고 객관적이라고 하는 수학이 엉뚱하게도 편견이나 직관적 오해를 강화하고 뒷받침하는 도구로 쓰인 사례들을 볼 수 있었다. 얼마 전에 통계청에서 정권에 유리하게 보이도록 통계의 발표 시기를 조절하거나 내용을 조정했다는 기사를 봤다. 한겨레 기사와 오마이뉴스에 실린 선대인의 글에 링크를 걸어 놓는다. 통계 자료의 항목이나 구간, 대상 기간 등을 조절해 전혀 다르게 보이는 통계 결과를 만들어낼 수 있으나 보통 사람들이 그걸 알아차리기는 힘들어서 (국정원은 본분이 정권의 개 노릇인지는 모르겠으나 적어도) 통계청은 중립적으로 일해야 할 절대적 필요가 있다고 한다. "심슨의 패러독스"(6장)에도 그런 통계의 맹점이 나온다. 통계나 확률의 오용을 막기 위해서라도 눈을 똑바로 뜨고 있어야 하는데... 솔직히 책을 옮겨 적긴 했는데 맞게 베꼈는지도 확실히 모르겠다;;;;