수학

수학을 배워서 어디에 쓰지?
이규영 지음 / 이지북 / 2021년 7월

놀라운 책입니다. 

저는 아이의 수학에 힘주게 되면서 새로나오는 수학 교양서를 많이 훑어보려 합니다. 이 책은 알라딘의 책소개 덕에 관심을 가지게 되었어요. 

 역사적으로 보면 수는 우리를 ‘귀찮게 하기 위해’ 태어난 것이 아니라, 철저히 ‘생존’과 ‘필요’, ‘쓸모’에 의해 만들어졌다. 『수학을 배워서 어디에 쓰지?』는 이런 수의 역사에 집중하여 사람들에게 필요한 것이 무엇인지 설명해 준다. 자연수, 허수, 무리수, 지수, 로그 등 수의 탄생 배경을 소개하면서 각각의 수가 필요한 이유를 보여 주고, 발전 과정을 소개하면서 그 수가 어떤 의미를 갖는지 알려 준다.

(알라딘 책소개)

 처음에는 그저 수학사 정도의 책으로 생각하고 읽기 시작했습니다. 그런데 저자의 해박한 지식과 수학적 해설, 맥락이 있는 전개가 정말 훌륭합니다. 올해 참 좋은 수학책을 많이 읽었다고 생각했는데, 이 책은 단연 탑이네요.^^

 바로 지인들에게 권하고 초등 고학년인 저희 아이와 여름방학 온책읽기 도서로 정했습니다.ㅎㅎ 아이가 저에게 귀찮게 물었던 의문들에 대한 답이 담겨 있거든요. 예를 들자면, 0은 왜 자연수가 아닌가, 1은 왜 소수가 아닌가, 1과 0.999...는 같은 수인가 다른 수인가 하는 질문들이요.

이 책의 저자 이규영님은 경영학을 전공하고 여러 권의 중,고등수학 교재를 집필하셨습니다. 이제까지 '중학수학 총정리 한 권에 끝내기', '고1 수학 한 권에 끝내기' 같은 수학 교재를 집필하셨는데, 유발 하라리의 '사피엔스'를 읽고 이 책의 아이디어 얻게 되었다고 합니다. 미래 기술에서 요구되는 수학 지식을 준비하기 위해서 '수'의 역사를 제대로 아는 것이 중요하다고 생각되어 이 책을 집필하셨다고 합니다.

저자는 이 책을 대수, 기하, 미적분, 통계, 이산수학 총 5권의 시리즈로 기획했다고 합니다. 벌써부터 다음 권이 기다려집니다.^^

이 책은 시리즈의 1권으로 '대수'를 다루고 있습니다.

수의 역사에 관한 방대한 내용이지만 골자만 적어본다면 이렇습니다.

1. 셀 수 없는 '양'에 단위를 도입하여 '수'로 인식하게 됨.

2. 수를 적기 위한 문자인 숫자를 만들고 숫자 체계를 정립하게 됨.

3. 수를 셈하게 됨 - 수를 자르고, 비교하고, 소수의 특성을 연구함.

4. 0과 음수라는 개념을 생각해냄. 

5. 사칙연산을 기호화하고 숫자를 문자로 일반화함.

6. 무리수와 허수를 수로 편입시켜 수의 차원을 넓힘.

7. 소수의 사용으로 무한의 개념을 가지게 됨.

8. 로그, 지수 등 큰 수를 생각케 됨. 

주욱 적으니 참 재미없게 느껴지네요.^^;

그러나 책 안에서 저자는 풍부한 역사적 자료와 이야기로 내용을 재미있게 이어가고 있습니다.

제가 이 책에서 얻은 정보 중 특히 흥미롭게 읽었던 부분을 몇 가지 소개해 보겠습니다.

1. 수의 발생

1-1. 양이 수로 편입됨

p. 158~159

셀 수 없는 것을 세는 기본 원리는 단위를 이용하여 단위의 몇 배로 나타내는 것이다, 문제는 주어진 단위보다 더 작은 대상을 세야 할 때다. 두 가지 방법이 있다. 하나는 더 작은 단위를 만드는 것이고 다른 하나는 새로운 표식을 만드는 것이다. 즉, 전자는 센티미터(cm)보다 작은 단위인 밀리미터(mm)  같은 단위를 만드는 것이고, 후자는 1/10과 같은 새로운 표식을 만드는 것이다, 여기서 후자의 방법은 분수이다.

(중략)

분수는 새로운 단위를 만들지 않고 기존의 단위를 계속 사용하기 위해서 '하나'를 자르는 표시법이라고 할 수 있다.

(중략)

상등을 이용하여 2개 이상의 분수의 분모를 같게 변신시키면서 분수의 덧셈과 뺄셈을 할 수 있게 되었다. 이로써 분수는 비로소 1보다 작은 양의 표식을 넘어서 온전한 '수' 취급을 받게 되었다.

저자는 셀 수 없는 양 (예를 들면 팔 길이, 땅의 넓이 등)을 세기 위해 단위가 고안되었고, 단위로 표현된 '양'을 연산할 수 있게 되면 비로소 '수'로 편입되게 됨을 설명합니다.

1-2. 비도 수였구나..

p. 214 

두 양 또는 두 수의 관계를 나타내던 비는 사칙연산이 가능한 분수를 만나 비율을 의미하게 되었고, 수로 인정받았다. 

2. 현대 수학의 약속들

2-1 셈 

저는 아이들이 학교에서 세로셈을 배우고 나면 더 이상 다른 방법은 생각해보지 않고 이 셈법만을 사용하는 게 참 아쉽습니다. 이 식을 보고 나니 현대수학이 세로셈을 발명한 이유가 있었네요. 한 자리 자연수만으로 곱셈이 가능하니 그랬던 거군요. 

2-2. 1의 소수성

p. 234~236

사실 1은 소수가 맞다. 더 정확히 말하면 소수로서의 성질, 즉 소수성을 가지고 있다. 현대수학에서 1을 굳이 소수에서 제외한 이유는 1이 가진 다음 특성 때문이다.

(중략)

이런 성질로 인해 1을 소수로 간주하면, 소인수분해의 결과가 여러 개 나올 수 있다.이렇듯 1은 한때는 소수였다가 지금은 필요에 의해서 소수의 지위를 빼앗겼다.

저의 아이가 항상 의문을 갖던 부분인데, 저는 그냥 '약속'이라고 하고 지나갔거든요. 이 책에서는 약속으로 정한 이유를 제시해서 제 가려운 곳을 긁어주네요.^^

2-3. 1/0의 해석

p. 249~251

수학에서는 1/0을 수로 인정하는 순간 1/0 *0은 1이 될 수도 0이 될 수도 있다. 이런 모순을 양자역학에서는 다르게 해석한다. 입자가 0 또는 1의 상태를 가진다고 할 때, 그 입자를 관찰하기 전까지는 0인지 1인지 정해진 것이 아니라고 주장한다.

이제까지는 불능이라고 배웠는데 양자역학이 더욱 연구되면, 이 부분이 새롭게 정의될 지 궁금합니다.^^ 직관적으로는 도저히 이해가 되지 않겠어요!

3. 교과서에서 배웠던 증명

3-1. 면적을 이용한 이차방정식의 해법

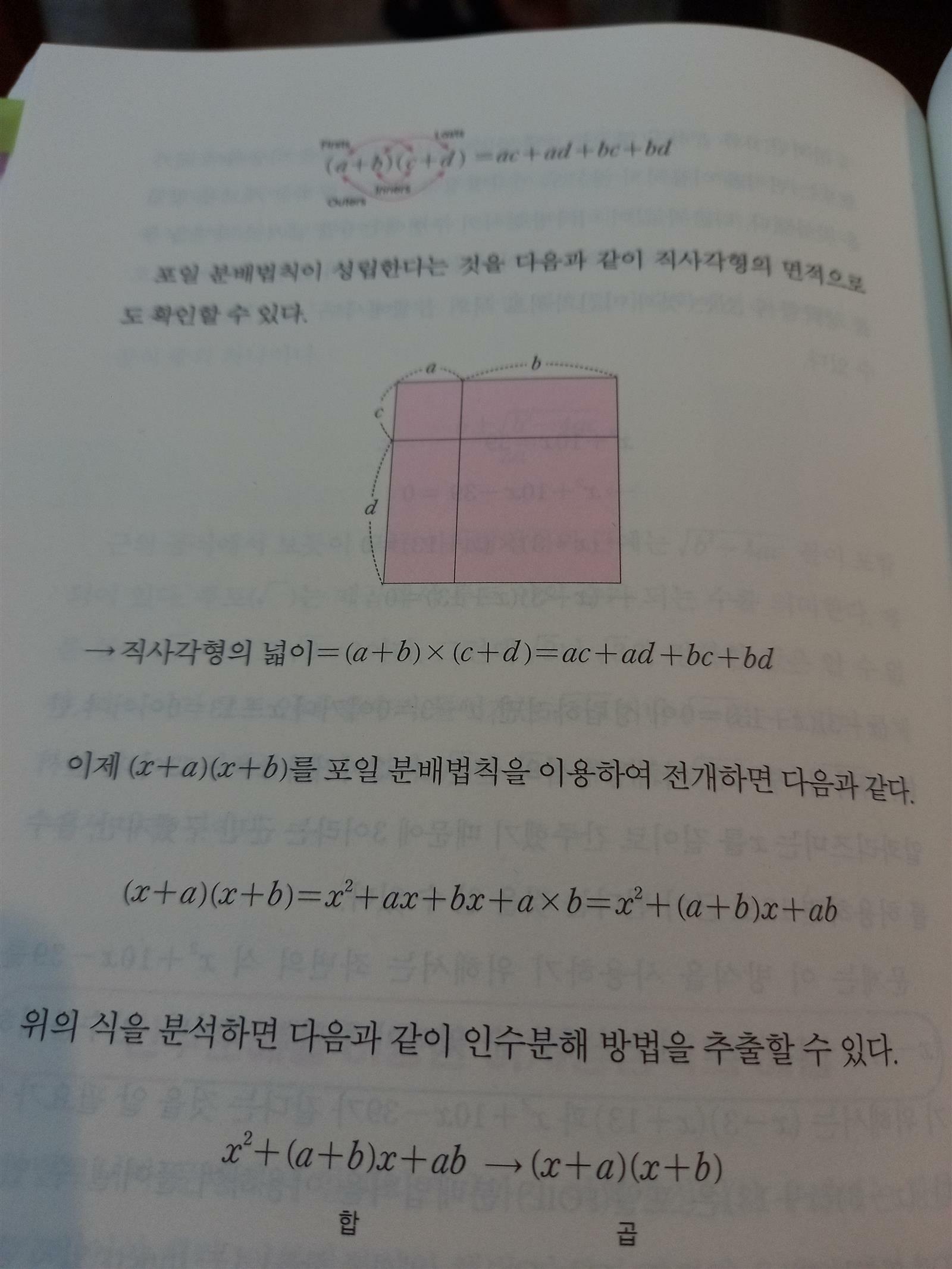
와, 이 방법은 천 년 전 아랍의 수학자가 쓴 책에 남겨진 방법이라고 합니다. 수식이 발달하기 전의 수학자들은 주로 기하를 이용해서 문제를 해결하곤 했나 봅니다.

3-2. 베셀의 기하적 해석

옛날 옛날에 교과서에서 쓱 보고 지나쳤던 거 같은 이 그림은, 놀랍게도 좌표 상에서 허수의 위치를 표현하는 데 사용되었습니다. 그저 두 닮은꼴 이야기였던 거 같은데.

고등수학을 공부하기 전의 학생들이 한 번씩 읽어보면 좋겠습니다. 수학에 대한 관심을 가지고 있는 일반인과 학부모께서도 읽어보면 좋겠고요. 제가 중고등학교 수학 선생님이라면 수업이 부교재로 사용하고 싶을 만큼 매력적인 책입니다.