겨울방학 선행학습은 개!념!탄!탄! 개념 해결의 법칙!! 초등수학문제집추천

개념 해결의 법칙 기초 수학 6-1 (2022년용) - 2015 개정 교육과정 ㅣ 초등 해결의 법칙 (2022년)
최용준.해법수학연구회 지음 / 천재교육 / 2018년 11월

겨울방학 선행학습은

개!념!탄!탄! 개념 해결의 법칙!!

초등수학문제집추천

겨울방학이 딱 3주 남았습니다

이번엔 봄방학 없이 쭈욱 겨울방학만 두 달하고

바로 신학기 시작이라 부담이 크네요..

이번 겨울방학은 자칫 어영부영하다간 폭망이다..

이런 생각이 자꾸 들고 조바심만 나네요.. ㅠ_ㅜ

특히 만두군은 예비 6학년이라 6학년 대비도 해야 하고,

코앞으로 다가온 중등 대비도 해야 하고.. ㅡ.,ㅡ

둘을 같이 해야 한다는 부담감은 넘쳐나는데

정작 아들은 아~~무 생각이 없어요

아무 생각이 없기 때문이죠.. 핫핫하.. ㅠ_ㅜ

겨울방학 시작하면 다음 학기 수학 선행 / 예습에 들어갔는데

그래서 이번엔 12월 초부터 조금 일찍 시작했습니다

만두군은 학원을 안 다니고 엄마표 홈스쿨을 하기 때문에

일정 조절이 쉽다는 장점이 있네요 ^^*

그동안 쭈욱 사용해왔던 천재교육 <개념 해결의 법칙> 으로

겨울방학 대비 선행학습 시작했어요 :)

개념 해결의 법칙 6-1

- 천재교육 -

내년 2019년에 2015 개정 교육과정에 의해

5, 6학년 교과서 개정이 이루어져요

2019년 <개념 해결의 법칙> 이 나오자마자 겟-!!! 해서

내년 6학년 과정을 살펴보았는데..

5학년 때 배웠던 것과 겹치는 것이 많네요

1단원 분수의 나눗셈, 3단원 소수의 나눗셈은

5학년 때 이미 배워서 개념 확인 위주로 학습 진행하고,

나머지 2단원 각기둥과 각뿔, 4단원 비와 비율,

5단원 여러 가지 그래프, 6단원 직육면체의 부피와 겉넓이는

아이들이 많이 어려워하고, 실수도 많은 부분이므로

교과서 개념 확실히 잡고 넘어가면 되겠네요 :D

<개념 해결의 법칙>

교과서 차시에 맞추어 쉽게 익히는

개념 중심 해결서

다음 학년을 위한 수학 선행학습을 시작한다?

그럼 저흰 제일 처음 시작하는 교재가

바로 <개념 해결의 법칙> 입니다 ^^*

#쉽고 #재미있게 #개념학습 #동영상강의제공

수학의 개념을 확실히 익히는 데에는

이만한 것이 없어요 ㅎㅎ

"학습만화는 훌륭한 수학 개념 공급원이죠"

만두군이 제일 좋아하는 학습만화 ㅎㅎㅎ

교재 받자마자 휘리릭 읽고 또 읽고..

​그렇게 읽다 보면 개념도 스르륵 머릿속에 들어와요

가끔 만두군이 아직 배우지도 않은 부분 알고 있어서

그걸 어디서 알았느냐고 깜짝 놀라 물어보면

학습만화 보다가 뭔지 궁금해서

개념까지 찾아보았다고 하더라고요 ^^*

학습만화는 봐도 봐도 질리지 않는다니 ㅋ

아이가 좋아하니 다음에도 꾸준히

<개념 해결의 법칙> 선택하게 됩니다 ㅎㅎ  

아이가 좋아하는 것이 학습만화라면!!

엄마가 좋아하는 것은 바로 동영상 강의!!

교재 내 QR코드를 찍기만 하면

동영상 강의, 유사문제 제공, 학습게임 등

천재교육의 다양한 콘텐츠를 만날 수 있어요  

<개념 해결의 법칙> 은 30일차 학습으로 구성되어 있어서

매일 꾸준히 학습하면 겨울방학 한달 동안

한 학기 수학 선행학습이 가능합니다 ^^*

저희는 <개념 해결의 법칙> 을 방학 동안 빡세게 풀고

방학숙제 선택 과제로 제출하고 그랬어요 ㅎㅎ

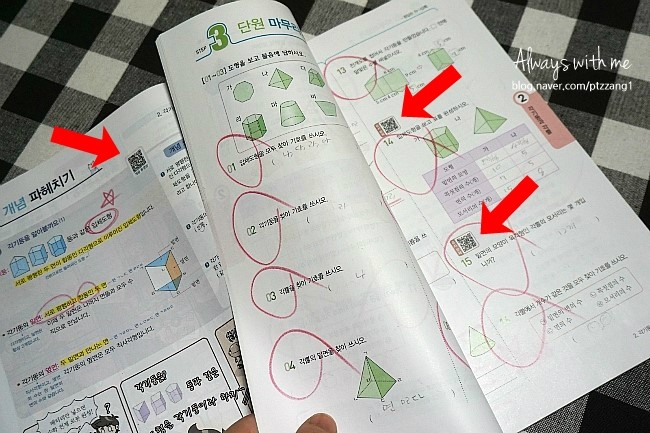
'개념 파헤치기' 로 교과서 개념 익히고~!!

'개념 확인하기' 로 개념을 내 것으로 만들고~!!

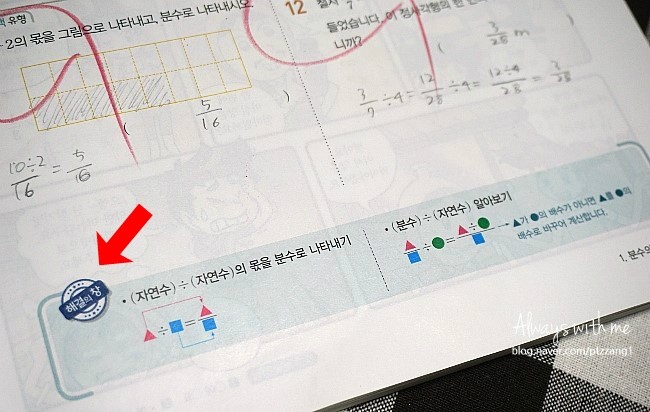
'해결의 창' 으로 꼭 알고 넘어가야 하는 개념 챙기고~!!!

꼭 알아야 하는 교과서 개념과

문제 풀이에 도움을 주는 개념들이 가득해서

<개념 해결의 법칙> 으로 학습하면

아이들 학업 성취에 도움이 됩니다 ^^*

<개념 해결의 법칙> 의 개념 설명은

딱딱한 글이 아닌 이미지를 통한 개념 설명이라서

아이들이 직관적으로 쉽게 받아들일 수 있고

보기 쉬우니~ 이해하기도 쉽고~

개념 이해는 덤으로 따라오는 거죠 ^^*  

개념 이해를 돕는 단계적 문제 풀이 이외에도

아이들의 창의사고력을 위한 창의 융합형 문제도 있어서

아이들이 다양한 유형의 문제에 어렵지 않게 접근할 수 있다는 것도

<개념 해결의 법칙> 교재의 큰 장점 중 하나입니다

1단원 분수의 나눗셈, 3단원 소수의 나눗셈은

5학년 2학기 때 이미 배웠지만

배웠다고 방심 말자~ 안다고 안 틀리냐~

틀린 문제 또 풀어보며 왜 틀렸는지

확실히 체크하고 넘어가요

<개념 해결의 법칙> 책 속 부록으로

'연산의 법칙' 이 들어 있어요

문제 풀 때 개념을 몰라서 틀린다기보다는

계산 실수, 연산 실수가 보일 때는

본책에 해당되는 부분 찾아서

관련된 연산 문제 풀어보며

연산 실수, 계산 실수를 줄일 수 있어요

단순히 교재에 나온 문제만 푸는 것이 아니라

이 문제는 왜 틀린 것인지 이유를 써보고

문제에 나온 개념의 뜻은 무엇인지

확실히 개념을 짚고 넘어가는 것이 중요합니다

개념 학습하고 확실하게 내 것으로 만드는 것..

엄마표 홈스쿨이니 가능한 것이죠 음홧홧하~~

틀린 문제는 답을 서술형으로 적어보아요

왜 그런 실수를 했는지 찾아내고

정확한 답을 구하기 위해서는

어떤 개념과 풀이 과정이 필요한지

적어보는 것이 제일 공부가 되거든요 ㅎㅎㅎ

3단원 소수의 나눗셈에 '몫을 어림하기' 가 나오는데

6학년 수학에서는 나누어지는 수를 어림한 다음에 계산하기 때문에

이건 5학년 때 배울 때보다 훨씬 쉬워졌다고 좋아하네요 ^^;;; 

5학년 때보다 쉬워진 6학년 소수의 나눗셈 ^^;;

단원 마무리 평가는 실수 없이 깨끗하게 백점 ㅎㅎ

그 어렵다는 4단원 비와 비율..

쉽게 개념 설명이 나와 있어도

자주 접하던 용어들이 아니라서 헷갈립니다

저도 봐도 잘 모르겠더라고요 ^^;;

비와 비율은 역시 어려워..

개념이 헷갈리고 실수하고..

그래서 와장창 틀리기도 했지만..

<개념 해결의 법칙> 의 교과서 개념을

다시 읽어보면서 절치부심!! 와신상담!!

헷갈리는 부분의 개념을 확실하게 짚고 넘어가요  

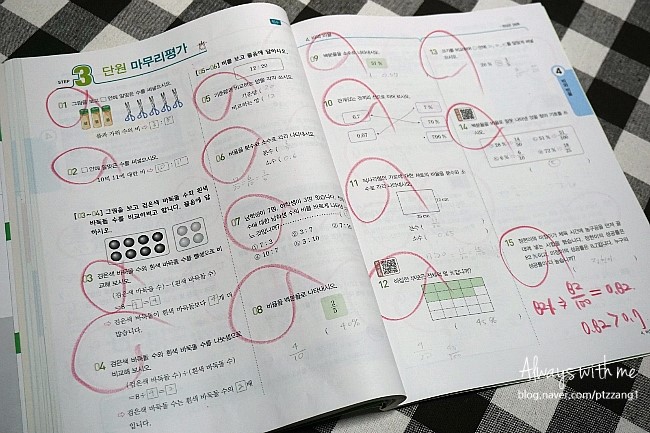
그 결과!!! 4단원 비와 비율 단원 마무리 평가도

올백으로 아름답게 마무~~으리!!!!

<개념 해결의 법칙> 학습을 12월부터 미리 시작해서

겨울방학까지 이어가려고 했는데

1단원 분수의 나눗셈, 3단원 소수의 나눗셈은

선행학습이라기보다는 복습이라 (5학년 때 배워서 ^^;;)

벌써 4단원 비와 비율까지 진도가 확확 나가버렸네요

이후로는 <개념 해결의 법칙> 마지막 단원까지 진도 나가고..

제일 헷갈렸던 부분은 동영상 강의 반복해서 보고

우등생 해법수학으로 다양한 유형의 문제 풀어보며

문제해결력 키워보려고 합니다 ^^*

음.. 이렇게 착착 계획 세워서 진도 빼니

이제 불안한 마음은 좀 가시네요 ㅎㅎㅎ

겨울방학 학습 계획은 안 세우셨다면

수학 선행학습은 필수이고요

<개념 해결의 법칙> 은 선택입니다 ^^*