중고생수학도서추천, 상상력과 사고력이 만들어낸 수학이야기

소름 돋는 수학의 재미 : 하편 - 공부 욕심이 두 배로 생기는 발칙한 수학 이야기 ㅣ 소름 돋는 수학의 재미
천융밍 지음, 리우스위엔 그림, 김지혜 옮김 / 미디어숲 / 2022년 2월

저번에 '소름 돋는 수학의 재미 - 상편'에 대한 포스팅을 한 적이 있습니다. 수학에 대한 수수께기 같은 호기심으로 무장한채 묵직한 내용들을 가볍게 풀어내는 책이어서 만족하면서 봤었습니다. 그런데 이번에 '하편'이 나왔다고해서 바로 접하게 되었습니다.

수학에 대한 흥미와 상상력 그리고 사고력을 키워주기에 좋은 책입니다.

상편 - 유리수, 무리수, 식과 방정식, 수열과 극한

하편 - 함수, 확률, 조합과 마방진, 집합과 논리

뇌를 자극하는 기발한 수수께끼가 가득한 책입니다. 흥미로운 문제로 시작하여 수학에 대한 상상력과 사고력을 키워주는 책입니다. 수학에 대한 흥미가 있는 친구들에게 좋을 책입니다. 개인적으로 이 책을 수월하게 이해하려면 고등수준의 수학적 지식을 가진상태에서 이 책을 보시는게 좋습니다.

이 책의 가장 첫번째 등장하는 이야기는 '페르마의 소수 공식'과 '메르센 수'에 대한 이야기입니다. 이 두 이야기를 통해서 우리가 알게 되는 것은 무엇일까요? 저는 개인적으로 이 두 이야기를 통해서 저자가 하고 싶은 이야기는 수학과 흥미와 열정을 가진 친구들은 여전히 많이 존재하고 그리고 그 모든 행위를 같이 즐기기를 원하고 있다라는 점을 말하고 싶은 게 아닌까 싶었습니다.

이런 열정과 흥미를 가진 이들의 교집합이 있기에 수학의 다양한 분야가 이어갈 수 있고, 그 중 하나는 이 책을 읽는 당신이 될 수 있다라는 점을 이야기하고 싶었던 것이 아닐까 싶었습니다.

1996년 초 미국 컴퓨터 수학자 조지 월트먼은 메르센 소수 계산 프로그램을 만들어 인터넷에 올려 수학자와 수학 애호가들이 무료로 이용할 수 있도록 하였습니다. 이것이 바로 '메르센 소수 합동 검색 프로젝트'입니다. 메르센 수를 찾기 위한 '협력화 운동'이 시작된 것입니다.

2018년 12월 7일 미국 패트릭 라로쉐는 이 프로젝트를 통해 51번째 메르센 소수

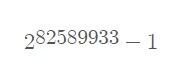
을 발견했습니다. 이 수는 모두 24862048자리로 이 책의 출간일까지 찾아낸 가장 큰 메르센 소수이자 가장 큰 소수라고 합니다.

수학, 과학뿐만 아니라 수많은 학문들의 가장 중요한 것은 바로 이렇게 누군가 계속 이어나간다는 게 아닐까 합니다.

스포츠경기에서 동전던지기로 서브권을 정하는것은 많이 봤지만, 글쎄 승부권까지 정한다는게 가능할까 싶은 생각이 첫번째 든 생각이었습니다. 이런 생각을 하는 저는 확률적인 부분을 잘 모르기에 그렇습니다.

그럼, 일반적으로 이 사안에 대해서 어떻게 생각을 할까?

'동전던지기로 승부결정'이라는 검색어로 검색을 해보면 생각보다 다양한 사례를 볼 수 있습니다. 그만큼 승부를 결정할 수 없는 경우에는 동전던지기를 통해서 결정하는 경우가 있다라는 것을 알 수 있습니다.

수학의 확률이라는 면에서 실험을 해보면, 동전 하나를 던져 앞면이 나올 가능성이 약 50%라는 우연한 사건의 법칙이 나옵니다. 그렇기에 동전을던져 서브권을 누구에게 줄 것인지 정하거나, 혹은 우열을 가리기 힘든 두 라이벌의 승패를 결정지을 수 있는 것이라고 합니다.

입장권 한장을 공평하게 가지기위해 추첨을 하기로 하는 세명의 아이들의 이야기를 통해서 과연 먼저 뽑는사람이 이득인가하는 문제를 다뤄봅니다. 엄마로서 저 이야기 읽으면서 아이들의 다툼을 해결하기 위해서 뽑기를 했던 기억이 문득 떠올랐습니다.

대부분의 사람들은 먼저 뽑는 사람이 이득이고, 나중에 뽑는 사람이 손해라고 생각을 합니다. 하지만 수학적으로 경우의 수를 따져보면 위의 그림의 도식에서 보다시피 각 1/3의 확률로 동일합니다. 따라서 마지막에 추첨을 한다고 해서 불리한 것은 아닙니다.

위의 그림처럼 그려보는 가지그림을 '수형도'라고 합니다. 수형도는 복잡한 실험문제를 해결하는 중요한 도구입니다.

가위, 바위, 보는 많은 이들이 무언가를 정하기 어려울 때 가볍게 승부를 낼 수 있는 방법입니다. 그렇다면, 이 게임에서 무승부가 날 확률은 얼마일까? 물론, 내가 상대에게 너무 뻔한 패턴을 보여주거나 속임수를 쓰거나 하는 예외적인 경우는 제외합니다.

2명이서 게임을 하는 경우와 3명이서 게임을 하든 무승부의 확률은 정확하게 같게 나옵니다. 1/3의 확률로 무승부가 나옵니다.

수학이라는게 참 흥미롭다는 생각이 들지 않나요? ^^

'출판사로부터 도서를 제공받음'

술과 인생 그리고 유쾌함, 애주가들을 위한 책 [개와 술]

개와술
쑬딴 지음 / 쑬딴스북 / 2022년 1월

술을 좋아하지만 잘 마시지는 못하는 일인으로서, 대리만족과 같은 심정을 느끼고픈 마음에 읽게 된 책입니다. 술과 인생 그리고 유쾌함이라는 이미지가 남는 책입니다. 정말 이분은 애주가가 확실하구나 싶은 생각도 들면서, 한편으로는 내 남편이라면... ... ... ... ... 글쎄... 뭐 이런 마음이 남는 책이기도 했습니다. 하지만 애주가들이라면 흔쾌히 유쾌하게 볼 수 있는 책으로 추천해봅니다.

술과 인생과 얽힌 짧지만 유쾌한 에피소드들을 담고 있는 책입니다. 장소와 환경은 국내로 국한되지 않고 세계적이어서 그 나라만의 문화나 환경적인 요소들이 묻어나기도 합니다. 그리고 그 나라 술에 대한 이야기와 얽힌 이야기들을 담겨져 있습니다.

각 나라에 대한 문화나 술에 대한 정보성 글을 기대하신분은 패스하시고, 애주가로서 즐겁게 애주가의 이야기를 듣고 싶다면 추천입니다.

각 에피소드들 마다 끝나고나면 관련된 술에 대한 삽화가 그려져 있습니다. 술을 잘 모르지만, 술을 잘 아는 애주가들에게는 이런 삽화도 매력적이지 않을까 합니다.

이 책을 다 읽고나서 든 생각이 작가분이 이 책을 왜 썼을까? 였습니다. 그러면서 떠오른 책 속 문장이 "난 마시고 싶다! 격렬하게 더 마시고 싶다!" 였습니다. 아마도 어쩌면 공적인 애주가로서의 더욱 더 입지를 굳히고자 하는게 아닐까하는 그런 생각이 문득 들었습니다.

이 책 곳곳에 작가분의 성격과 생각이 묻어납니다. 이탈리아에서 겪은 상황도 어찌보면 평생의 좋지않은 일로 기억할만도 한데, 그 기억을 좋은기억으로 바꾸는 그런 생각의 힘을 가진 분이라는 생각이 들었습니다. 그리고 중간에 '인터미션'에 나오는 개와 술에 대한 담백한 이야기에 저도 모르게 빵 터지고 말았습니다. 모두가 마음에 담고 있는 말이지만 공적으로 쉽게 내뱉지는 못하는 말인데, 너무나도 담백하게 뱉어내고 있었습니다.

'인터미션'에서는 책 제목이 '개와술'인데 왜 개 이야기는 첫 장에만 등장하는지에 대해서 담백솔직하게 이야기하고 있는 부분입니다.

맨 마지막장의 아내을 위한 특별페이지도 재미있었습니다. 아내분의 협박(?)아래에 나온 페이지이지만 아내가 저자분에 대해 느끼는 생각을 알 수 있었습니다. 저는 저자분의 술에 대한 사랑을 아내는 어떻게 바라볼 지 솔직히 궁금했었습니다.

술에 대해서 솔직담백하고 유쾌한 이야기를 읽어내려가보픈 이들에게 좋을 책입니다.

'출판사로부터 도서를 제공받음'

6가지 이야기로 담아보는 다양한 SF장르 소설, [너의 다정한 우주로부터]

너의 다정한 우주로부터 ㅣ 오늘의 젊은 문학 4
이경희 지음 / 다산책방 / 2022년 1월

개인적으로 단편소설보다는 장편소설을 좋아하는 편입니다. 그래서 이 책이 장편이었다면 더 좋았을텐데라는 생각으로 읽기 시작한게 사실입니다. 하지만 읽어내려가면서 오히려 단편소설집이라는 점이 더 매력적인 SF장르소설집이었습니다. 우리가 생각하고 기대하는 SF장르 그리고 SF같지 않은 SF장르 등등 다양한 SF장르를 맛 볼 수 있었습니다.

SF장르의 맛집 투어라고 생각하고 보시면 즐거운 시간을 보낼 수 있을 책입니다.

"장르에 대한 사랑으로 응집한 SF 소설집"

책을 읽고나니, 이 문장이 이 책을 정확하게 나타낸다는 생각이 듭니다.

총6편의 단편으로 이루어져 있습니다.

우리가 죽어도 끝나지 않은 이야기 속에서

이지용(문화평론가)

[우리가 멈추면]에서 보여주는 지극히 현실적이고 사회적인 메시지들로부터 출발해, [살아 있는 조상님들의 밤]에서 나타나고 있는 시대의 관습들과의 문제에 다다르게 되면 소설들이 이야기하는 문제들이 지극히 현실적인 지금 우리로부터 나타나고 있음을 알 수 있다. 이후[다층구조로 감싸인 입체적 거래의 위험성에 대하여] 에서는 현실의 문제들은 메타포로 급격하게 치환되면서 SF가 가장 잘 만들어낼 수 있는 경이의 세계들로 진입하고 있다는 것으 느낄 수 있다. [바벨의 도서관]가 [신체강탈자의 침과 입]은 기존의 SF가 가지고 있던 온갖 상징들을 알고 있다면 더 풍부하게 즐길 수 잇는 전형적인 장르물이고, 그렇지 않다고 하더라도 이야기가 주는 유쾌함을 따라 즐기는데 아쉬움이 없다. 이윽고[저 먼 미래의 유크로니아]에 도착하면 SF가 갈 수 있는 최대한의 시간과 공간의 개념들을 과감하게 돌파하는 작가의 필력에 감탄하면서 긴 시간을 유영하게 된다.

각 작품에 대해 가장 잘 설명을 하고 있는 부분이라서 옮겨봅니다.

---

개인적으로 가장 흥미로웠던 이야기는 [다층구조로 감싸인 입체적 거래의 위험성에 대하여] 였습니다.

"내 모습은 내가 욕망하는대로 변하고, 세계는 내가 말하는 대로 바뀐다!"

우리가 일반적으로 원하는 미래세상은 이런게 아닐까하는 생각이 듭니다. 우리가 미래사회에서 원하는 것.

'레디 플레이어 원' 영화가 절로 생각나는 그런 대사였습니다. '우리가 원하는 무엇이든 될 수 있다'와 맥락을 같이 한다는 생각입니다. 그럼 이런 미래에 사는 이들의 삶은 어떨지 궁금해질 수 밖에 없습니다. 막상 들여본 세상은 모든것이 엉크러진 상태입니다.

"사람들이 욕망하는 게 다들 다르니까. 현실이 한가지 형태로 고정되지 못하고 계속 일그러지는 거예요. 중심지 빌딩들은 항상 이런 식이죠. 쳐다보는 사람이 너무 맣아서 욕망이 끊임없이 충돌하는 거예요."

"욕망구현장치가 탄생한 이후로, 인간들은 그저 천박하게 욕망을 채우기 급급했어. (...) 욕망할 수 있는 모든 욕망을 욕망한 끝에 그들은 가능한 모든 욕망을 고갈시키고 말았어. 더는 충족시킬 욕망이 사라지자 수많은 사람들이 목숨을 끊었어. 인류는 삶을 이어갈 동력을 순식간에 잃어버리고 만 거야."

"궁지에 몰린 인간들은 위험한 선택을 했어. 스스로 욕망하기를 포기하고, 대신 욕망을 탐구해 줄 인공지능들에게 자신의 운명을 맡겼어. (...)생성적 적대 알고리즘에 따라 생성자인 너는 새로운 욕망을 생성했어. 감별자인 나는 네 욕망에 인류를 위협할 요소가 내포되어 있는지 예측했고, 만약 네가 내 예측모형을 속이고 통제를 벗어나려 한다면 그땐 ."

"우리를 둘러싼 샌드박스가 모든 것을 초기화시켜."

*샌드박스 : 프로그램이 허용되지 않는 영역까지 영향을 미치지 못하도록 격리된 공간을 생성하는 보안 조치.

디스의 주머니에서 10경 1038조 3718억 1903만 7652개의 코인이 쏟아졌다. 진이 갖고 있었던 10만 5876개와는 비교도 되지 않을 정도로 월등히 많은 양이었다. 진은 자신이 왜 그러는지도 모른 채, 바닥을 기어다니며 허겁지겁 코인을 쓸어 담았다. 세상에 존재하는 모든 코인을 가졌음에도 진은 도저히 만족할 수 없었다. 그저 더 많은 코인을 탐요가하게 될 뿐, 달라지는 것은 아무것도 없었다. 코인은 고갈된 욕망이었다. 이제 새로운 욕망이 필요했다.

---

요즘 우연치않게 SF관련 영화와 다큐멘터리를 보고 있던 상황이라서 그런지 좀 더 몰입하면서 보게 된 것 같습니다. 그리고 이 세상을 이루는 주체가 인간이라면, 그것도 지금과 같은 상태의 인간이라면 미래가 슬플 가능성이 더 높겠구나 하는 생각이 듭니다.

[우리가 멈추면]에서 소행성의 자원광물을 지나치게 착취한 결과 궤도에서 벗어나게 되는 그런 상태를 만들어 냅니다. [우리가 멈추면]의 내용은 지금의 사회문제를 그대로 우주로 가져온 경우입니다. '인간의 기본적인 면이 변하지 않으면, ...' 이런 생각이 자꾸만 들던 내용이었습니다.

SF장르의 다양한 소설을 보고 싶다면 추천하고픈 책입니다.

'출판사로부터 도서를 제공받음'

메타버스에 대한 전체적인 이해를 돕는 [디지털 신세계 메타버스를 선점하라]

디지털 신세계 메타버스를 선점하라 - 앞으로 인류가 살아갈 가상 세계를 위한 새로운 경제 패러다임
자오궈둥.이환환.쉬위엔중 지음, 정주은 옮김, 김정이 감수 / 미디어숲 / 2022년 1월

이 책은 메타버스에 대한 전체적인 이해를 돕는책입니다. 좋은 면 뿐만 아니라 해결되어야 하는 구체적인 사안에 대해서도 상세히 설명을 돕고 있습니다. 그리고 현재 우리가 가야하는 메타버스방향과 궁극점 그리고 현재 우리는 어디까지 와 있는지에 대한 방향과 기술에 대한 부분도 상세히 설명을 들을 수 있습니다.

메타버스와 함께 등장하는 탈중앙화, 가상화폐와 같은 부분이 왜 많은 이들의 이목을 끌게 되었는지에 대해서도 상세하게 다루고 있습니다.

이 책을 읽으면서 정보비대칭을 이루는 독과점사회의 대안이 될 수 있을까라는 의문이 남기도 합니다. 그러면서도 결국 지금의 시점에서 가야할 방향이라는 부분은 명확한데 가는길이 쉽지는 않겠구나 하는 생각도 듭니다. 해결되어야 할 문제들이 여전히 많고 그리고 결론적으로 정부의 개입에서 자유로운 어느정도의 탈중앙화에 다가가는 것이 정말 가능할까 싶기도 합니다.

개인적으로 메타버스의 이상향보다 왜 메타버스에 열광하게 되었는지에 대한 인간의 심리적인 면부터 경제적인 면 그리고 그 과정에 어떤리스크들이 따르고 어떤 문제들을 해결해야만 하는지에 대해서 구체적으로 다룬점 때문에 메타버스라는 숲만 보는것이 아니라 그안에 나무들도 좀 더 자세히 볼 수 있었습니다.

위의 내용을 읽으면서 가장 눈에 들어오는 것은 함께 만들고, 함께 누리고, 함께 관리한다 입니다. 기존의 시스템에서 함께 만들고 누리는 것은 가능하지만 함께 관리한다는 아직까지 도달하지 못한 부분입니다. 이 부분에서 저는 메타버스라는게 결국 인간의 욕망을 대신하는 그런 부분이 아닌가 합니다. 기술적인 부분도 역시 마찬가지이지만 가장 큰 부분은 인간의 심리적인 욕망이라고 생각합니다.

누군가가 독점하고 관리하는 세상이 아니라 누구에게나 평등하고 공정한 그런 세상을 원하는 욕망에서 출발한 것이 메타버스가 아닌가 합니다.

현재 모든 경제체제는 탈중앙화를 꿈꾸고 있는 상황입니다. 중앙화라는 편리성을 누리는대신 그로인한 정보편취문제로 인해서 공평하지 못한 체제를 겪은 이들의 작은 반항으로 시작이 되는 듯 합니다. 많은 이들이 꿈꾸는 탈중앙화에는 어떤 문제가 따라올까라는 부분도 생각해봐야 하지 않을까합니다. 정말 그들이 생각하는 공정하고 평등한 사회가 만들어 질 수 있을까 하는 문제입니다.

하지만 결국 디지털화폐라는 문제가 남아있고, 그 디지털화폐의 안정화와 법적인 문제는 중앙화를 거칠 수 밖에 없습니다. 디지털세상을 이미 겪고있는 우리는 그 속의 세상이 정말 공평하다고만 생각이 되지는 않습니다.

새로운 세상이 열리는 것은 맞지만 그 속에서 또 다른 계층이 만들어지는 것은 아닌가 하는 생각도 듭니다.

메타버스경제의 기초는 창작을 기반으로 합니다. 그리고 창작자와 소비자간의 공정한 화폐이동이 이루어지며 그 모든것은 현실세계와 통용되기도 합니다. 이때 떠오르는 대부분은 아마 게임일 것입니다. 실제로 로블록스는 메타버스세상의 초기세상으로 불리고 있습니다. 로블록스에서 플레이어로서만 이용할 수 있지만, 그 속에서 사용자들은 누구나 창작을 할 수 있습니다. 그리고 그 속에서 그에 따른 화폐이동이 일어납니다. 그리고 그 화폐는 일정금액 안에서 현실통화로 교환이 가능합니다.

메타버스 세상에서 빠질 수 없는 부분은 경제입니다. 그렇기 때문에 메타버스경제와 연결된 가상화폐는 발전할 수 밖에 없습니다. 하지만 여전히 맹점이 남아있는 상황이라서 이런 부분을 어떻게 해결하고 어떤규범으로 통제할지도 고민입니다.

nft에 대해서는 여러가지 논란이 많은 상황입니다. 디지털화폐는 사회적규범속으로 들어오고 있는 흐름이지만 nft는 아직까지 확실하게 사회적규범속으로 들어오지는 못한 상황입니다. 이런 혼란한 상황속에서 옳은방향으로 나아가면 안정성을 갖출 수 있지만, 옳지 않은 방향으로 나아가는 흐름이 더 강하다면 기술적인 부분만 취하고 나머지부분은 버려질 가능성도 있습니다.

전세계가 대부분 물질풍족사회라는것에 대해서는 누구도 반박할 수 없을 듯 합니다. 그러면 더이상 욕구는 물질로만 채워질 수 없습니다. 물질로만 채워질 수 있다면 더 많은 물질을 가진 지금의 사회를 구성하는 구성원들은 과거보다 분명 행복해야 합니다. 하지만 실제로 과거보다 사람들의 행복감은 더 떨어지고 불안감은 더 높아졌습니다.

회사에서 월급을 받는 조건으로 충성을 맹세하던 그런 시절이 지나고 이제는 제대로 된 평가와 인정을 바라고 있는 시대입니다. 그런 M세대가 정신적인 인정을 받고 공평한 세상을 꿈꾸기에 메타버스로 향하고 있는 중입니다.

메타버스는 현실세계를 뭐든지 할 수 있는 디지털세상으로 옮겨간 형태입니다. 그 속에서 어느정도의 규범과 원칙이 필요할 것이고 그런 속에서 어딘가에 데이타가 모일 수 밖에 없을 듯 합니다. 메타버스화폐는 어느정도의 규제가 필요할 것이고 그 역할은 아무래도 국가가 할 가능성도 있습니다.

누구나에게 똑같이 공정, 평등, 경제, 창작, 환경, 화폐 세상이 주어져서 현실보다 나은 세상이 될 수 있을것인지? 아니면 그냥 현실세계의 확장판일 뿐일지?

---

'무슨 일이든 할 수 있기 때문이지만 여기 머무르는 것은 무엇이든 될 수 있기 때문이다.' 개인적으로는 메타버스 세상이 이렇게 되기를 바랍니다. 단순히 공상과학이 아니라 앞으로 맞이할 세상이자, 많은 기업들과 기술들이 이곳을 바라보는 중입니다.

어떤 리스크가 있고 어떤 낙원이 있을지 양면성을 알아보고 현 기술과 기업들이 어디까지 와 있는지 알아보는 책으로 추천합니다.

개인적으로 청소년들도 이해가 가능하다면 읽어보면 좋을 듯 합니다.

'출판사로부터 도서를 제공받음'

결정과 선택이 항상 어려운 이들에게 [선택과 결정은 타이밍이다]

선택과 결정은 타이밍이다 - 1%의 미련도 남지 않게 최선의 선택과 결정을 하는 법
최훈 지음 / 밀리언서재 / 2022년 1월

어떤분들은 이 책을 보면서 이렇게 선택과 결정이 어려운 사람이 있을까하면서 의문을 제기하는 사람도 있을거고, 같은 이유로 항상 힘들어하기에 공감하는 분도 있을거라 생각이 듭니다.

저같은 경우는 팬데믹 상황과 작년에 의도치않게 건강에 이상에 생기는 등의 사건등을 겪으면서 많이 달라졌습니다. 굳이 말하자면, 바뀌기전의 상황 즉, 코로나이전상황의 저의 모습과 이 저자분의 과거 모습과 굉장히 닮았습니다. 책을 읽다가 보니 MBTI성향이 같았습니다. 같은 MBTI를 가진 둘째아이가 현재 이 속에 갇혀서 힘들어하고 있겠구나하는 생각도 들었습니다.

이 책은 선택과 결정에 있어서 항상 머뭇거리게 되고, 선택과 결정을 하는데 있어서 자기자신보다 다른이들의 상황을 먼저 고려하게 되고, 선택결정후에 다른 선택지에 대한 후회를 가지고 과거를 자꾸 돌이켜보게 되는 그런 이들에게 도움이 될 책입니다.

"여러분은 과거로 돌아갈 수 있다면 어느시점으로 돌아가고 싶으신가요?"

책의 중간에 이와 관련된 이야기가 나옵니다. 예전에는 되돌아가고 싶은 시점이 너무 많아서 하나만 선택할 수 없을 정도였습니다. 하지만 지금은 현재를 살고싶지 과거로 돌아가고 싶은 마음은 별로 없습니다. 그리고 지나간 과거에 대한 후회보다는 현재를 어떻게 살아낼 것인지에 대한 생각이 훨씬 많아진 상황입니다.

이 책의 저자분도 그렇고 저도 그렇고 왜 예전에는 선택과 결정을 못하고, 매순간 후회하고 망설이고 그렇게 답답함과 잘못된 억울함을 가지고 살았을까요? 정말 똑같은 이유였습니다. 자신의 삶에 있어서 가장 중요한 '나'가 없었습니다.

모든 선택과 결정에 있어서 자신이 무엇을 원하고 있는지를 알지 못했습니다. 자신을 제외한 모든 상황들만 고려한 채 이루어지다보니 항상 모든일에 후회가 남고, 선택하지 않았던 선택지에 대한 미련이 항상 남을 수 밖에 없었습니다. 타인의 입장에서서 오히려 소통 하지않고 혼자서만 세상을 사는 사람으로 보이는 오해를 받는것도 사실입니다.

모든것은 스스로의 상태를 인지하는것에서부터 시작이 됩니다. 신중함과 결정장애는 분명히 틀립니다. 신중한게 아니라 결정장애라고 판단이 되면 그 결정에 있어서 '나'라는 존재가 혹시 빠지지는 않았는지 체크해봅니다. 정말 내가 원하는 것이 맞는지, 이 선택지가 주변환경을 위한 것이 아니라 정말 나를 위한 선택지가 맞는지 말입니다. 그리고 그 이후의 과정에서 후회가 있을수도 있다는 점을 미리 인지합니다.

나의 배우자가 혹은 나의 아이가 이런 성향을 가지고 태어날 수 있습니다. 또는 내 자신이 이런 사람일 수도 있습니다. 그렇다면 어떤 배려를 스스로 또는 상대방에게 해주는게 좋은지 알고 있으면 대처하기가 좀 더 쉽습니다. 최소한 얼굴 붉히는 상황이나 상대방의 답답함을 조금이나마 덜 수 있습니다.

인생의 답은 자기자신에게 있습니다. 내가 누군지? 내가 어떤 사람인지? 내가 어떤 성격을 갖고 있는지? 내가 어떨 대 행복하고 즐거움을 느끼는지? 스스로를 이해하는 것부터 시작해야 합니다. 자신을 알게되면 어디를 향해가야할지 방향을 정해볼 수 있습니다. 그러면 다른환경이나 상황에서 조금은 덜 흔들릴 수 있는 그런 주도성을 가진 사람에 가까워질 것입니다. 그런과정을 거치면서 자신이 하나하나 선택해온 선택지들이 자신의 삶을 만들어 나갈것이고, 주도성을 가진 선택을 했기에 후회도 조금은 덜 할 것입니다.

---

자신이 신중하고 배려깊은 삶을 산다고 생각한다면, 자기체크를 그래도 한번은 해봐야 할 것 같습니다. 정말 신중하고 배려심이 깊은건지 아니면 나의 인생이 아니라 남의 인생을 대신 살아준다고 정신이 없는건지 말입니다. 스스로 못 느끼는 경우가 많습니다. 특히나 어린시절부터 그런 학습이 되어온 상태라면 더욱 더 말입니다.

"여러분은 삶은 평안하신가요?"

스스로에게 한번씩 물어봐야 할 질문이 아닌가 합니다.

'출판사로부터 도서를 제공받음'