사춘기 소녀의 설레는 이야기

열두 살이란 말로는 어려워 ㅣ 라임 향기 도서관 7
이성 지음, 김정미 그림 / 가람어린이 / 2013년 7월

세번째 만나는 가람어린이의 라임향기 도서관시리즈..

7번째 책인듯 한데.. 3권을 만나보았다.

딸냄의 나이가 12살..

딱 맞는 시기의 소녀들의 풋풋한 첫사랑과 사춘기를 다루는지라 

엄마는 호기심으로 아이 엿보기를 할 수 있고..

딸냄에겐 설레임으로 다가갈 수 있는 시리즈다.

요즘 엄마나, 친구와 여러가지 트러블로 부딪히기 시작한 딸냄..

아무래도 사춘기가 시작될 징조가 아닌가 싶다.

열두살이란 말로는 어려워..란 제목으로 그래서

딸냄에게도 엄마인 내게도 다가왔다.

사춘기 중에서 요 책은 설레는 첫사랑과 이성에 대한 관심을 더 다루고 있지만..

아직 딸냄은 까칠함에 주를 두고 이성은 덜 관심을 보여서

앞으로 주인공 나리처럼 딸냄에게 찾아올 이성친구들에 대한 예습도 되었던 책이다.

멋쟁이 한새가 좋아하는 아이가 반에서 이쁘고 공부도 잘하고

착하진 않지만 부자인 유진..이라는 소식에 좌절하는 아이의 모습이

사춘기면 누구나 겪는 이야기로 보여서 눈이 갔다.

이쁘게 보이기 위해 다이어트도 하고..

남친이 있으면서도 맘을 몰라주는 단짝 친구에 대한 미움으로 답답해도 하고....

전학간 영규와 메일친구가 되었다가

두 남자 친구 사이에서 방황하는 원치않던 삼각관계에 빠지기도 하고,

마냥 이쁜 대학생 언니를 부러워도 하고..

딸냄과 책을 읽고 작은 다툼을 벌이기도 했다.

핸폰을 사준지도 얼마되지 않았지만,

처음 약속을 잊고, 카톡을 깔겠다고 해서 투닥거리는 중이었고...

이젠 반 아이들이 밴드란걸 가입했다고하여

메일도 만들고 싶다고 하던 중이라서..

요 책 속의 메일 친구와 주고받은 메시지에 마냥 부러워하면서

모든 아이들이 하는 걸 못하게 한다고 투덜대는 딸냄에게

안되는 이유를 대느라 고생했다. ㅋㅋ

울 딸과 비슷한 아이 나리의 이야기..

사춘기 딸냄의 설레이는 다양한 상황이 궁금하다면..

재밋게 만나보면 좋을 시리즈다.

올림포스 12신을 찾아라-그리스신화 게임북

올림포스 12신을 찾아라 - 한눈에 쏙쏙! 그리스신화 게임북
장지선 지음, 임성훈 그림 / 케이론북스 / 2012년 10월

그리스로마신화를 좋아하는 아이들..

어렸을때도 장난감보다는 게임북으로 놀았던지라..

월리를 찾아라..처럼 숨겨진 그림찾기도, 틀린그림 비교하기도 넘넘 사랑한다..

책이 오자마자 게임북인데다 그리스로마신화 내용이니

 얼른 집어든 딸냄..

덕분에.. 삐진 동생과 잠시 실랑이를 하고...

같이 숨겨진 켄과 아이템 찾기에 골몰..

미술관에 놀러왔다가 그리스 신화 속 12신의

그림을 만나 신화 세계에 갖힌 책이 탈출하려면..

숨어있는 그림들을 모두 찾아야한단다..

사이좋아진 남매는.. 중간중간의 그리스로마신화에도 관심가득..

신화속의 다양한 신들의 이야기.. 계보..

그리고 인간과의 에피소드..

미술관 속 이야기이기에..

각종 유명한 조각상과 신들의 이야기를 담은 세계의 명화들도 나와있다.

제우스가 신의 시작인줄 아는 아들냄과 달리..

그리스로마신화를 자주 읽어서.. 가이아와 우라노스, 크로노스의

신들의 계보부터 아는 딸냄의 잘난척이 이어진다.. ㅋㅋ

신화속의 신들은 잔인한 면이 상당하다.. 사실 그 내용엔

숨겨진 의미가 있지만..

책을 통해..숨겨진 의미를 파악하면 신화라 불리는 이야기를

더 잘 알 수 있다.

아이들이 한참을 놀았던.. 주사위놀이..

여러 보드게임을 가지고 있어서 많은 주사위가 도움이 된다..ㅋㅋ

요 책 하나로 아이들은 한참을 행복한 시간을 보냈다.

사이에 숨겨진 그림 찾기 만이 아니라 틀린 그림 비교하기도 있었고..

다양한 즐거움이 있다.

아이들끼리 정해진 그림을 설명하고 찾아보기 게임도 가능..

책으로도 읽고.. 이젠 놀이도 할 수 있는 책..

올림포스 12신을 찾아라..

곧 휴가철인데.. 그곳에 들고 간다고 해도

아이들을 즐겁게 해줄 책이다.  

신통방통 전통의례

신통방통 플러스 전통 의례 ㅣ 신통방통 사회 5
김진섭 지음, 강윤정 그림 / 좋은책어린이 / 2013년 5월

꼬맹이가 좋아하는 신통방통 시리즈.. 특별히 엄마의 맘에 들었던

우리나라 시리즈에 이어서 나오고 있는 신통방통 플러스는..

아이에게 다양한 지식을 재밌게 전달한다..

오자마자.. 손에 들고 읽어대는 아이들을 보면 흐뭇하기만 하다.

이번에 만난건 신통방통 플러스 전통의례..

전통의례란 말조차 낯선 아이가 어떻게 받아들일지.. 설명없이 책을 건넸다.^^

책 사이사이에 있는 지식전달로 아이는 전통의례가 무엇인지, 제례,관례,상례,혼례의 의미를

설명해 줄 필요없이 스스로 알아가면서 읽어나갔다..

세 분의 할아버지의 이야기를 통해 하나씩 배워가는 의례들..

사실 제례는 제사려니..하던 엄마의 짧은 지식과 달리..

 제사 자체가 아닌 제사를 지내는 예법이란 뜻이란다..

홍동백서등등의 제사때 할머니가 중얼거리는 말들의 뜻도 아이는 하나씩 알아나갔다.. ^^

돌찬치도 하나의 예법.. 아이가 잘 자라 훌륭한 사람이 되라고 하는 것인데..

삼신상도 차린다고 재밌어했다.

자기가 어릴적 돌잡이에 쌀을 잡았다면서 한참을 누나에게 이야기했고..ㅎㅎ

하나하나 삼촌의 혼례와 세 할아버지중 한분 수염 할아버지의

상을 치르게 되면서 안타깝지만... 상례까지 배웠다..

책의 이야기 사이 사이 이런 지식전달 부분의 정리가 있어서 오늘날과 원래 과거의

전통의례도 비교하면서 알 수 있었다.

재밌다면서 두번을 읽은 아들냄.. 마인드 맵으로 오늘 배운 것을 정리.. ^^

쉽지 않은 전통의례.. 다양한 예절을 아이는 재밌게 쉽게 알게 되었던

즐거운 신통방통 플러스 전통의례이야기 였다. 

알콰리즈미가 들려주는 이차 방정식 이야기

알콰리즈미가 들려주는 이차방정식 이야기 ㅣ 수학자가 들려주는 수학 이야기 14
김승태 지음 / 자음과모음 / 2008년 3월

디오판토스가 들려주는 일차 방정식 이야기 http://blog.naver.com/han3995/50172421234 를 만나고

저학년부터 해온 모르는 수를 네모로 둔 각 종 연산들이 일차 방정식으로 이어진다는 것과 아이들이 어렴풋이 이미

배웠지만 활용이 힘들었다는 것을 알고.. 신선한 수학의 재미에 빠졌었기에..

이번엔 이차방정식을 만나봤다..

학창시절 정말.. ㅋㅋ 많이 욕했던 "누가 만든거야? 근의 공식" 의 주인공 알콰리즈미가 들려주는 이차방정식 이야기..

스스로 뿌듯해하는 알콰리즈미가 들려주는 이차방정식은 생각보다 쉽게 풀어져 있어서..

중고등 수학을 접한지 한참임에도 이차방정식의 의미와 그 풀이 과정이 새록새록 떠오르는 즐거움이 있었다.

물론 사이사이 문제에선.. 그에게 수업을 듣는 정식이 처럼 헉.. 하기도 했지만..ㅎㅎ

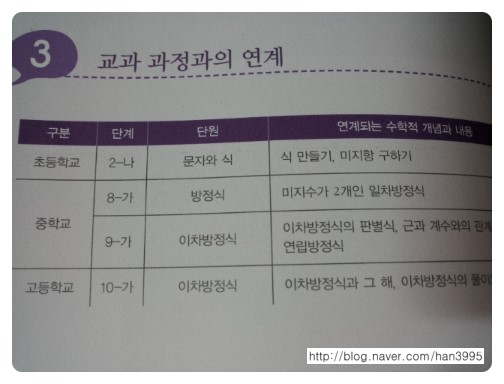
초등학교때의 문자와 식이 중학교때의 방정식과 이차방정식으로..

그리고 고등학교때의 이차방정식으로 연결된다.

중학교 때까지의 이차방정식과 고등의 차이는 허수를 인정한다는것.. 근과 해가

없다라고 한 것이 생겨서 어려워진 것이 기억이난다..ㅎㅎ

알콰리즈미..사실 낯선 인물이었는데.. 요것을 보니 알겠다. 피타고라스의 정리도 책 속에서

나오긴 하지만.. 일단 답은 5번..

책의 사이사이..이차방정식의 의미, 등식, 방정식, 항등식, 이항, 동류항,

해, 근, 정수, 인수분해, 판별식, 실근, 허근, 완전제곱식, 제곱수, 차수, 무리수, 황금비,

계수, 차수, 중근, 피타고라스의 정리, 루트, 제곱근, 유리수, 연립이차방정식, 대입법, 가감법, 이원, 소거..

등의 용어를 다시 만나면서 머리도 아팠지만..ㅋㅋ 일차방정식서 다시 확인한 수학의 연산법과

잊고 있던 계산법을 다시 떠올릴 수 있었다.

각단원별로 학습목표와 미리 알고 있어야할 지식..그리고 마무리에 수업의 정리를

통해서 한 단원에서 다룬것을 정리해보는 것이 아주 깔끔해서 맘에 쏘옥 .. ^^

신기했던 중국산 수학.. ㅎㅎ

구장산술에서 만난 이차방정식의 문제는 정말 신선했고, 다시 만난 그리스의 수학자

디오판토스의 묘비 문제도 등장..

무리수의 정의를 만화로 만나니 기호의 의미와 만들어진 이유를 알기 쉬웠네요.

요런 만화가 참 깔끔하게 정리해주고 있는 요 책..맘에 든다..

 

초등학생이 이해할만한 내용에서 시작해서 고등수학까지 살짝 맛본 책 이차방정식..

마무리의 알콰리즈미의 말처럼.. 처음부터 쉽진 않지만 자주 접하고

많이 풀어서 익숙해진다면 편리하게 사용할 수 있는 이차방정식..^^

다음엔 또 수학자가 들려주는 어떤 수학이야기를 만나볼지.. 벌써부터 두근두근하다. 

탈레스가 들려주는 닮음 이야기 - 수학자가 들려주는 수학이야기 09

탈레스가 들려주는 닮음 이야기 ㅣ 수학자가 들려주는 수학 이야기 9
나소연 지음 / 자음과모음 / 2008년 2월

5학년 딸냄의 수학 1학기 5단원은 도형의 합동..

도형을 유난히 어려워하는 딸냄에게 흥미도 높이고, 도형의 합동에서 더 나아가 닮음을 통해 2학기의

비율까지 만나볼 수 있도록 탈레스가 들려주는 닮음 이야기를 만나봤다.

기본적으로 합동외에도 다양한 도형의 지식을 기본으로 깔고 있어야하기에 초등 고학년에서부터

읽으면 적당할 듯 보이지만.. 수학을 좋아하는 아이들이라면 사이사이 설명이 잘 되어 있어서

배우지 않은 단원이라도 기본개념을 만나볼 기회도 될 듯하다.

탈레스가 들려주는 닮음의 이야기는 부천의 명소.. 아인스월드를 배경으로 하고 있다.

1/25로 축소한 세계의 다양한 건물들을 만나볼 수 있는 아인스월드..

런닝맨에서 나온적도 있고.. 사실 어릴적엔 가본적도 있는 공간이라 몰입도도 높았다.^^

아는 곳에 대한 이야기라 호기심이 더한듯..

http://terms.naver.com/entry.nhn?cid=247&docId=947784&mobile&categoryId=247 

일상생활에서의 닮음과 수학의 닮음은 조금 다르다는 것부터 시작해서

확대와 축소를 통해서 변화되었을때 똑같이 겹치는 것이 수학의 닮음이란

이야기를 축소 에펠탑으로 풀어주었다.

합동에서 배운 대응각, 대응변을 이용해..합동처럼 같은 각과 같은 비율을 가져야

닮음이 된다는 것도 알았고. ^^

닮음의 중심이 되는 중심점으로 부터 일정 비율 떨어진 닮은 도형을 통해

알고 있는 변의 길이와 닮은 모르는 변의 길이도 구했고,

중학교에 배울 SSS, SAS, AA합동과 닮음이란 용어도 만났다.

같은 위치의 각, 등으로 4학년때 만났던 평행 수직을 통한 각의 크기는

역시 동위각, 엇각, 맞꼭지각이란 용어를 통해 만나면서 다시 한번

정리해볼 수 있었다.

모르는 단어 닮음비도.. ^^

중점을 연결해서 닮은 삼각형을 그리면  모르는 변의 길이를 구할 수 있다는 것..

그리고 지금 학교서 배우는 도형의 넓이와 연결되어진 닮은 도형의

둘레의 길이이의 비, 넓이비, 부피비 까지..

사실.. 아직 아이가 정확히 모르는 비와 비율을 알면.. 더 많은 계산까지 쉽게 이해했겠지만..

비와 비율을 배우지 않은 딸냄도, 이런식으로 비교하는 구나..란 비의 개념까지

알게 해준 닮음 도형이었다고나 할까..

넓이비로 피자주문시  미디엄 두판과 라지 한판중에서 선택하는 걸 보고

재밌어하는 딸냄..

현실에서 이용되는 닮음비의 활용에 요즘 실생활에 연관되어진 수학문제가

많아진 만큼 더 관심이 가는 예시였다..

수학자가 들려준다고 해서.. 어려울지 모른다는 오해는 풀자.. 수학자가 설명해서

개념부터 더 쉽고 재밌게 다가가지는 깊이있고, 넓은 시야를 가지게 되는

수학도서..  왜 권하는 사람이 많은지 새삼 생각할 수 있던 책이었다.. ^^