수학실험을 통한 흥미로운 수학이야기

수학, 풀지 말고 실험해 봐 - 신기한 실험으로 수학과 친해지기 ㅣ 수학, 풀지 말고 실험해 봐 1
라이이웨이 지음, 김지혜 옮김 / 미디어숲 / 2021년 7월

수학이 재미없고 어렵기만 하다면 흥미를 느끼는 것이 먼저!

수학의 재미를 알게 하는 수학실험이 담긴 '수학, 풀지 말고 실험해 봐' _ 신기한 실험으로 수학과 친해지기

수학은 어렵습니다. 사실은 어려운 것이 아니라 어렵다는 인식 때문에 흥미가 떨어지고 떨어진 흥미로 수학을 접근하다 보니 어렵지 않아도 마치 어려운 것처럼 여겨지며 싫어하는 순서를 밟아가는 것이 아닐까 생각됩니다. 적어도 지금까지의 수학은 말입니다. 하지만 이제 산수에서 수학으로 넘어가는 시기에 자녀들을 둔 분들이라면 더 이상 수학이 재미없고 어려운 것이 아니라는 것을 알고는 계실 것 같습니다. 그것을 뒷받침해줄 만한 도서들이 끊임없이 나오고 있고 이번에 소개할 『수학, 풀지 말고 실험해 봐』도 그 도서 중 하나입니다. 이미 수학이 재미없고 어렵기만 하다고 느껴버린 아이들에게 먼저 해줄 것은 흥미를 느끼게 해주는 것이라고 합니다. 이에 수학의 재미를 알게 하는 수학실험 15가지가 수록되어 있는데요. 일상생활 속에서 만나는 흥미로운 수학! 이미 알고 계신 그것이 수학이었다는 것을 깨닫게 되는 데는 많은 시간이 필요하지 않답니다.^^

수학을 공부하지 않은 대부분 사람들에게는

믿기지 않게 보이는 일들이 있다.

아르키메데스

『수학, 풀지 말고 실험해 봐』 차례

『수학, 풀지 말고 실험해 봐』 에서는 모두 15가지의 수학실험이 수록되어 있습니다. 차례 제목만 보아도 어려워 보이지 않고 일상생활과 크게 다를 바 없음을 알 수 있죠? 과연 어떤 이야기로 수학에 대한 흥미를 돋워줄지 기대가 됩니다.

『수학, 풀지 말고 실험해 봐』 케이크의 크기는 어떻게 잴까?

케이크를 조각내어 분수를 공부하는 방법은 이미 익히 알려진 방법입니다. 그런데 크기가 다른 케이크의 비교는 어떨까요? 6인치 케이크가 4인치 케이크의 몇 배인지 입으로 한 입 한 입 베어 먹으며 그 크기를 가늠하는 것 말고 좋은 방법은 없을지에 대한 접근으로 시작됩니다. 여기서 원하는 방법은 케이크의 크기를 먼저 부피로 계산하는 것입니다. 케이크는 보통 원통 모형이므로 원기둥의 부피(원기둥의 밑넓이 × 높이)를 계산하는 것입니다. 어렵다고요? 저도 여기까지는 그냥 수학이네~ 라고 생각했습니다. 하지만 실험으로 흥미를 유발해 봅니다.

케이크 크기와 같은 모형을 준비하고 물을 부어 표시선으로 구분하는 방법입니다. 수학은 우리의 많은 시간을 절약할 수 있게 도와줍니다. 이것이 수학의 힘입니다. 머리를 써서 수학을 공부하는 대신 손을 써서 공부하는 실험! 첫 실험부터 아주 간단하죠?

『수학, 풀지 말고 실험해 봐』 동그란 꽃 한 송이

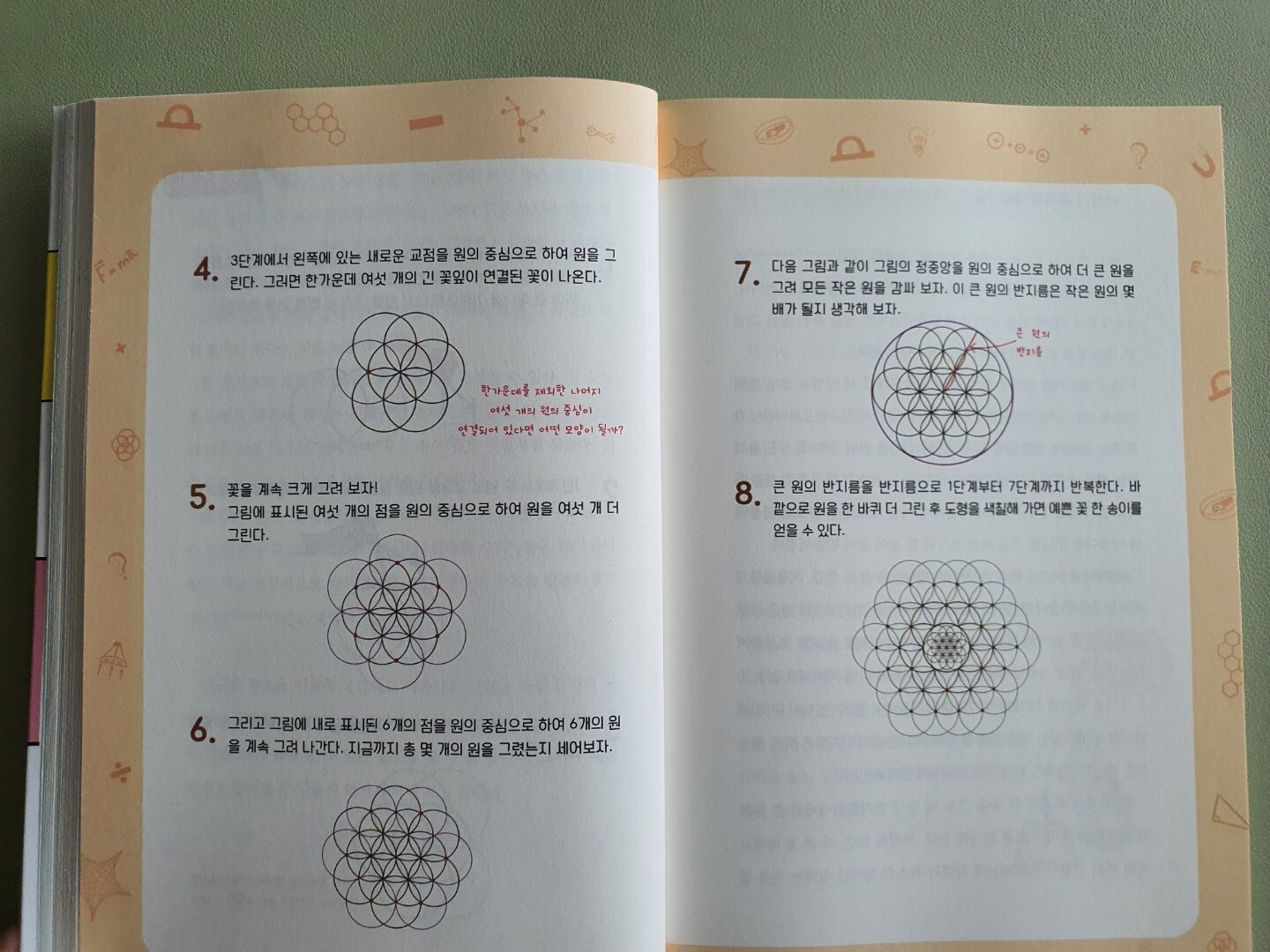
초등학교 4학년이 되면 컴퍼스를 사용하는데요. 이 컴퍼스가 단순히 원을 그리는 것에서 끝나는 것이 아니라 여러 원을 이용하여 아름다운 꽃 한 송이를 완성할 수 있다고 합니다. 그 원리는 바로 이것입니다.

콜리플라워와 고사리 잎에 숨겨진 규칙!

같은 크기의 원을 여러 개 그리다 보면 아름다운 꽃 한 송이가 완성이 됩니다. 회장님맘은 해바라기처럼 보이네요^^ 도화지와 컴퍼스 하나만을 가지고 멋진 도안이 되는 것 같죠? 아주 간단하게 꽃을 정교하게 그리는 방법 배우셨죠?^^

『수학, 풀지 말고 실험해 봐』 직선으로 꽃을 그려 보자

꽃에 유독 진심인 회장님맘은 꽃 그리는 것에 푹 빠져듭니다. 앞서 원으로 꽃을 그렸는데요. 이번에는 직선으로 꽃을 그려보는 시간입니다. 상식적으로 직선으로 그려진 꽃이 어떤 모습일지 떠오르지 않죠? 바로 흔히 볼 수 있는 네모난 벽돌로 쌓은 아치형 문이나 직육면체 모양의 벽돌들이 호 모양으로 된 바닥이 그것입니다. 네모반듯하고 굽어진 부분이 없는데 둥근 모양을 만들 수 있는 실험! 보실까요?

점과 점을 이은 선으로 만든 별꽃송이! 어디에도 곡선은 없는데 직선이 곡선이 되어 꽃이 완성되는 놀라운 마법 같은 일을 직접 경험해 보시면 좋을 것 같네요^^

『수학, 풀지 말고 실험해 봐』 신기한 뫼비우스 띠

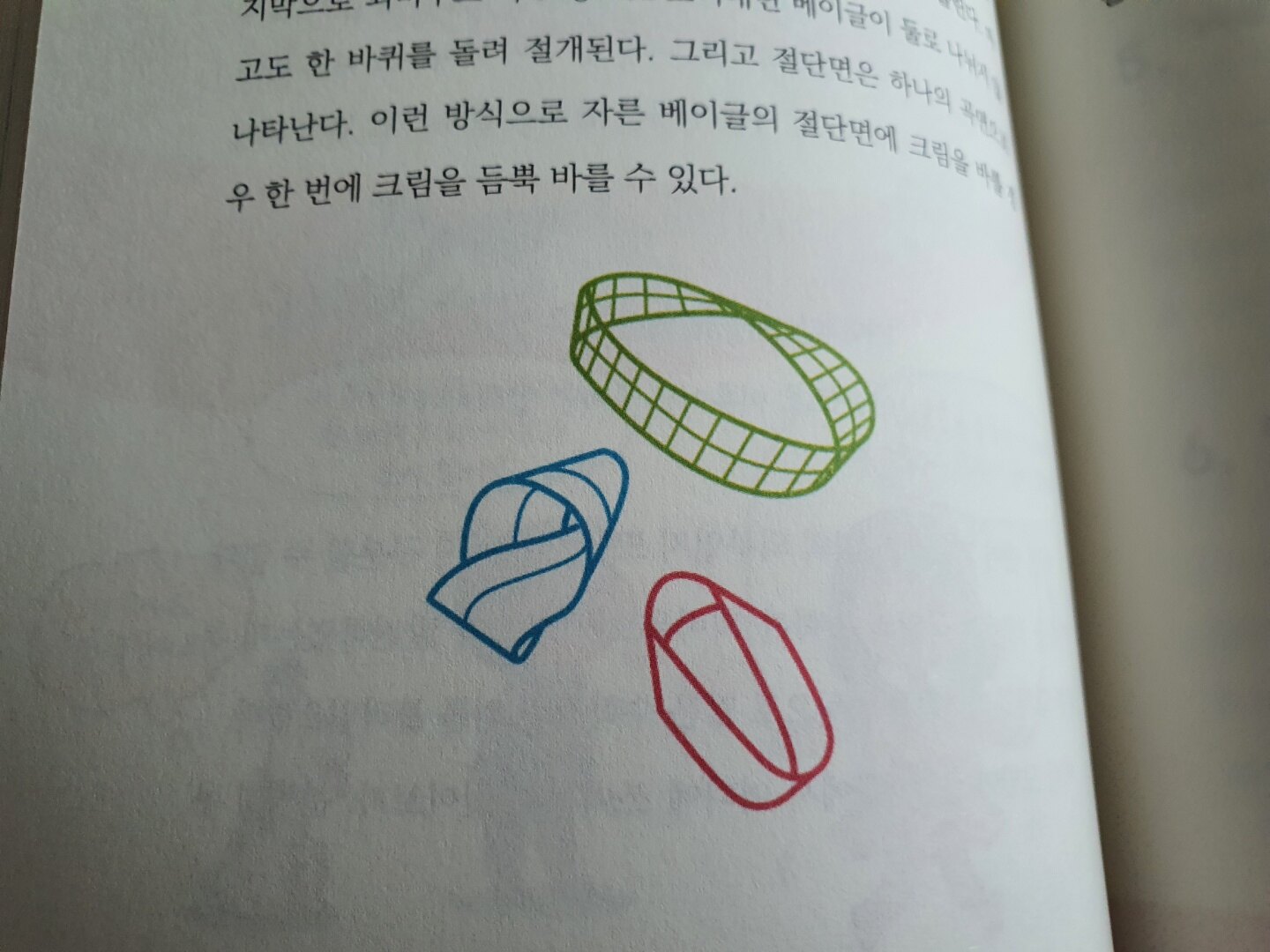
이미 뫼비우스 띠는 아시는 분이 많으실 텐데요. 돌고 도는 평면! 수학의 세계에서 두 평면을 가지는 입체도형의 모습! 실제로 이를 이용하여 리본을 만드는 경우도 많이 볼 수 있습니다. 돌고 돌아도 끝이 없이 도는 뫼비우스 띠. 얼마 전 바하가 학교에서 방과후로 수리과학 수업에서 만들어왔다며 신기한 듯 설명하던 게 눈에 선하네요. 뫼비우스 띠는 내외부의 경계를 없애고 하나의 면을 이룹니다. 그렇기에 우리의 생활 속 여러 곳에서 활용되고 있는데요. 국제 순환 재건 로고와 구글 클라우드 로고를 자세히 보면 뫼비우스 띠임을 확인할 수 있습니다. 특히 예술가들이 뫼비우스 띠에 관심을 보이며 착시현상을 이용한 모습을 볼 수 있습니다.

색종이로도 간단히 뫼비우스 띠를 만 들 수 있습니다. 바로 이 장면이 바하가 보여준 수리과학 수업입니다. 뫼비우스 띠 하나를 만든 뒤 가위를 이용하여 중앙선을 자르면 당연히(?) 두 개의 띠가 나올 것이라고 예상하지만 결과는 다르죠. 바로 원래의 모습보다 2배 길어진 띠가 만들어지는 실험! 이 실험은 본인이 하면서도 본인이 놀라는 실험이라고 할 수 있습니다. 실제로 바하가 이미 학교에서 해보고 와서 보여주는데도 본인이 신기하다며 연신 감탄사를 내뱉기 바빴으니까요^^;;

『수학, 풀지 말고 실험해 봐』 수학 속으로...

우리가 알고 있는 수학보다 더 많은 이야기를 품고 있는 수학! 그 수학을 사랑한 사람들의 이야기를 들어 볼 수 있는 『수학, 풀지 말고 실험해 봐』의 '수학 속으로'입니다. 실제 눈으로 보거나 손으로 만질 수 없는 수학의 추상성이 수학을 어렵다고 느끼는 가장 큰 원인이라고 합니다. 이젠 일상에서 수학을 만나다 보면 더 이상 지루하지 않고 재미있는 수학이 되지 않을까 생각됩니다.

가볍게 읽고 아이들과 함께 실험해 보며 수학에 대한 흥미를 높이는 도서 『수학, 풀지 말고 실험해 봐』를 이 세상의 모든 사람들에게 추천합니다.^^