쉽다는데 쉽지 않은 책

미적분의 힘 - 복잡한 세상을 푸는 단순하고 강력한 도구
스티븐 스트로가츠 지음, 이충호 옮김 / 해나무 / 2021년 9월

더하기, 빼기, 곱하기, 나누기를 배운 이후 분수를 배우기 시작하면서

뼛속까지 문과가 되기로 결심한 저는 방정식 단계부터는 수학을 홀대한 터라

'미적분'이란 단어는 그저 남의 나라 것인 줄 알았습니다.

한자로만 보면 미분微分은 잘게 나눈다, 적분積分은 계속 쌓는다는 뜻 정도로만

알고 있었지요.

뭐 그래도 사는데 아무 지장 없었으니까요.

[미적분의 힘]을 읽겠다는 생각이 든 것은 왜 일까요?

'복잡한 세상을 푸는 단순하고 강력한 도구' 책을 소개하는 글을 읽는 순간

이 책을 한번 읽어봐야겠다는 생각이 들었어요.

이 책을 읽기 전 미적분의 개념은 조금 알아야 할 것 같아서 찾아보니

미분은 연속적이고 지속적으로 변하는 사물의 속도를 측정하는 방법이고

적분은 아주 작은 양을 여러 번 합산하는 연산법이라는 설명이 있었습니다.

도대체 이걸로 어떻게 복잡한 세상을 푼다는 것일까요?

극한은 미묘한 개념이지만, 미적분학의 핵심 개념이다.

극한 손에 잡힐 듯하면서도 잘 잡히지 않는 개념인데,

일생생활에서 흔히 접하는 개념이 아니기 때문이다.

<1장 무한> 中에서

극한이란 개념이 나왔습니다.

원의 둘레값을 구하기 위해 원을 잘게 잘게 쪼개야 하는데

쪼개면 쪼갤수록 원의 둘레값에 가까워지기 때문이라고 합니다.

극한은 도달할 수 없는 목적지와 같아서 그곳에 점점 가까이 다가갈 수는 있지만

절대로 그곳에 이를 수 없는 것이나 다름없죠.

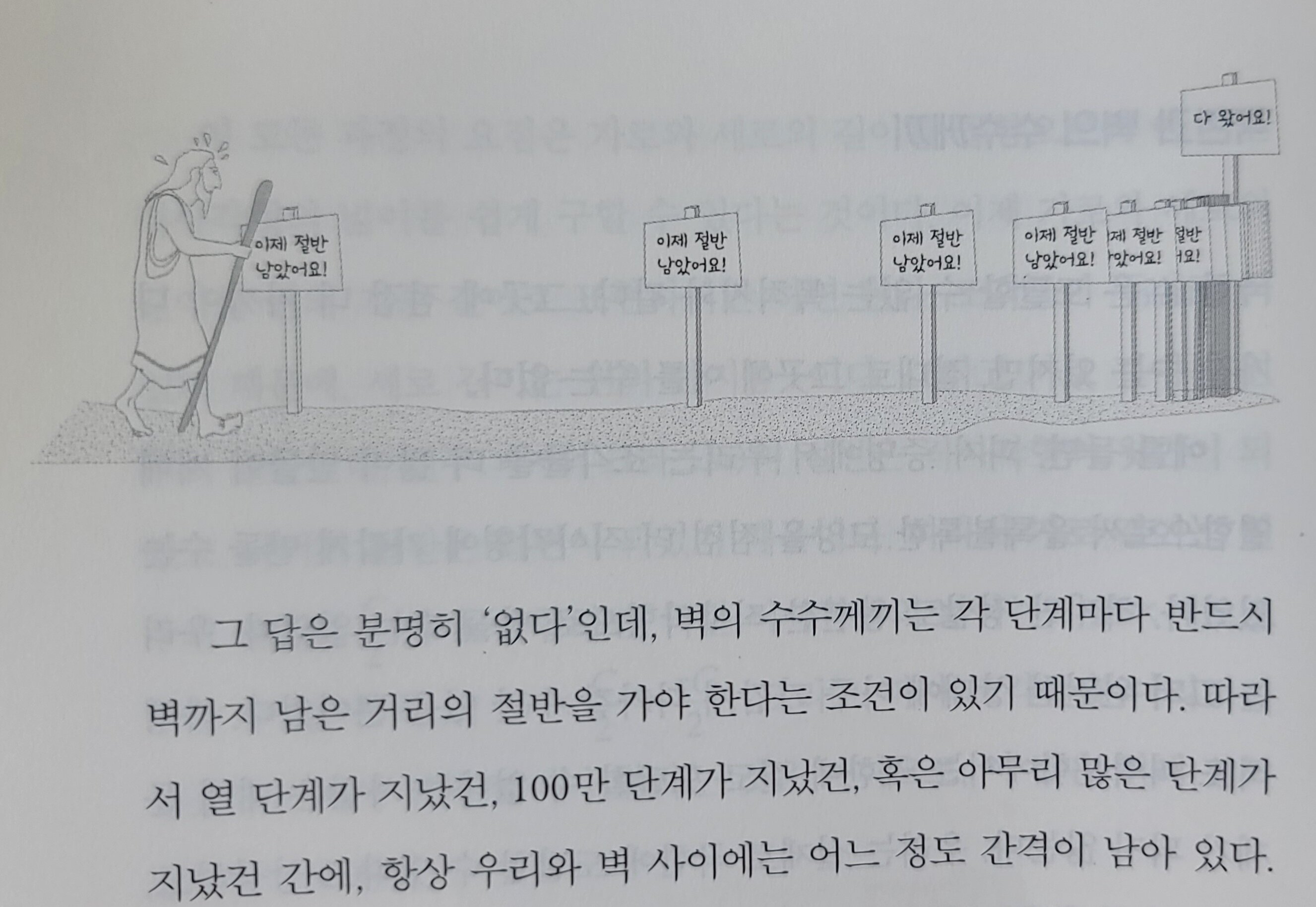
이 사실을 잘 설명하는 것이 '벽의 수수께기'였습니다.

'제논의 역설'에서 설명하는 아킬레스와 거북 역설을 떠올리게 했습니다.

물론 저는 이 역설을 몇 번이나 설명을 들었지만 참 어렵네요.(웃음)

하지만 이런 미적분을 가장 잘 이해할 수 있었던 것은

아르키메데스가 포물선 활꼴을 찾으면서 무한히 많은 삼각형 모자이크를

사용했던 일화를 통해서였습니다.

바로 애니메이션에서 이용되는 다각형 덕분에 곡선의 형태가 완성되었다는 것이죠.

뾰족 뾰족한 삼각형이 만드는 부드러운 곡선은 둥근형과 달리

쪼개면 쪼갤수록 오히려 더 유연하고 매끄럽게 구부러질 수 있다는 점이 놀라웠습니다.

이것이 바로 미적분의 힘인가요?

이렇듯 책의 전반은 미적분이 일상에 어떻게 적용되고 있는지를 잘 설명해주고 있습니다.

멀리서 보면 넓고 커다란 숲이지만 가까이서 보면 나무 한 그루, 풀 한 포기로 이뤄져 있듯

지구와 태양계 나아가 무한한 우주도 원자와 입자들로 이뤄져 있음을 알게 되는 것처럼요.

중간 크기의 은하 안에서 떠다니는 하찮은 행성에 살고 있는 하찮은 종인

우리 호모 사피엔스는 어떻게 10억 광년 너머의 먼 우주에서

두 블랙홀이 충돌한 뒤에 시간과 공간이 이런 식으로 흔들릴지 알 수 있었을까?

우리는 그 중력파가 이곳에 도착하기도 전에 중력파가

어떤 소리를 내야 하는지 알고 있었다.

그리고 미적분학과 컴퓨터와 아인슈타인 덕분에 우리의 계산과 예측이 들어맞았다.

<미적분의 힘> 中에서

고행같은 책이었어요.

이 책에 대해 "당신이 언젠가 미적분학을 배우고 싶었다면, 그 언젠가는 바로 지금이다"

라는 문장 때문에 읽었는데 저는 '지금'이 아닌가 봅니다.

하지만 적어도 전 원주율 파이의 값이 어디에서 나왔는지는 비로소 이해할 수 있게 되었어요.

그 정도만 해도 이 섬세한 책에 대해 저는 만족합니다.

미적분의 세계가 궁금하다면 조금 어렵지만 [미적분의 힘]을 읽어보시면 어떨까요?