수학의 미래 초등 2학년 1학기 예습 서술형 사고력 문제집

수학의 미래 초등 2-1 ㅣ 초등 수학의 미래
전국수학교사모임 미래수학교과서팀 지음 / 비아에듀 / 2020년 12월

1학년 2학기가 끝나고

월요일부터 겨울방학에 들어가요.

이제 3월부터 규씨는 2학년이 된답니다.

국어, 수학은 학원을 다니지 않고 홈스쿨 중인

규씨에겐 제가 선택하는 문제집의 영향이 커서

하나에만 치우치지 않고 다양하게

풀어볼 수 있도록 노력하는 편이에요.

다양하게 풀리다 보니

규씨도 본인에게 맞는 문제집인지 아닌지

느낌이 오는가 보더라고요.

"이건 재밌네~" 하는 문제집이 있는가 하면

어떤 문제집들은 다음엔 안 풀고 싶다고

정확하게 얘기해 주기도 하거든요.

예비 2학년 규씨를 위해 선택한

내가 주인공이 되는 수학 개념 교과서

『수학의 미래』는 어떨지 궁금하네요~

수학의 미래 머리말에 보면

아래와 같이 글이 있어요.

"수학이

인공 지능, 첨단 의학, 스마트 시티,

자율 주행 자동차, 항공 우주 등

제4차 산업혁명의 심장이 되었다.

21세기 산업은 수학이 좌우할 것!"

영국 총리 직속 연구위원회 보고서 中

일상에서의 수학적 사고를 할 수 있는

능동적 발견자가 되어야 한다는 것이죠.

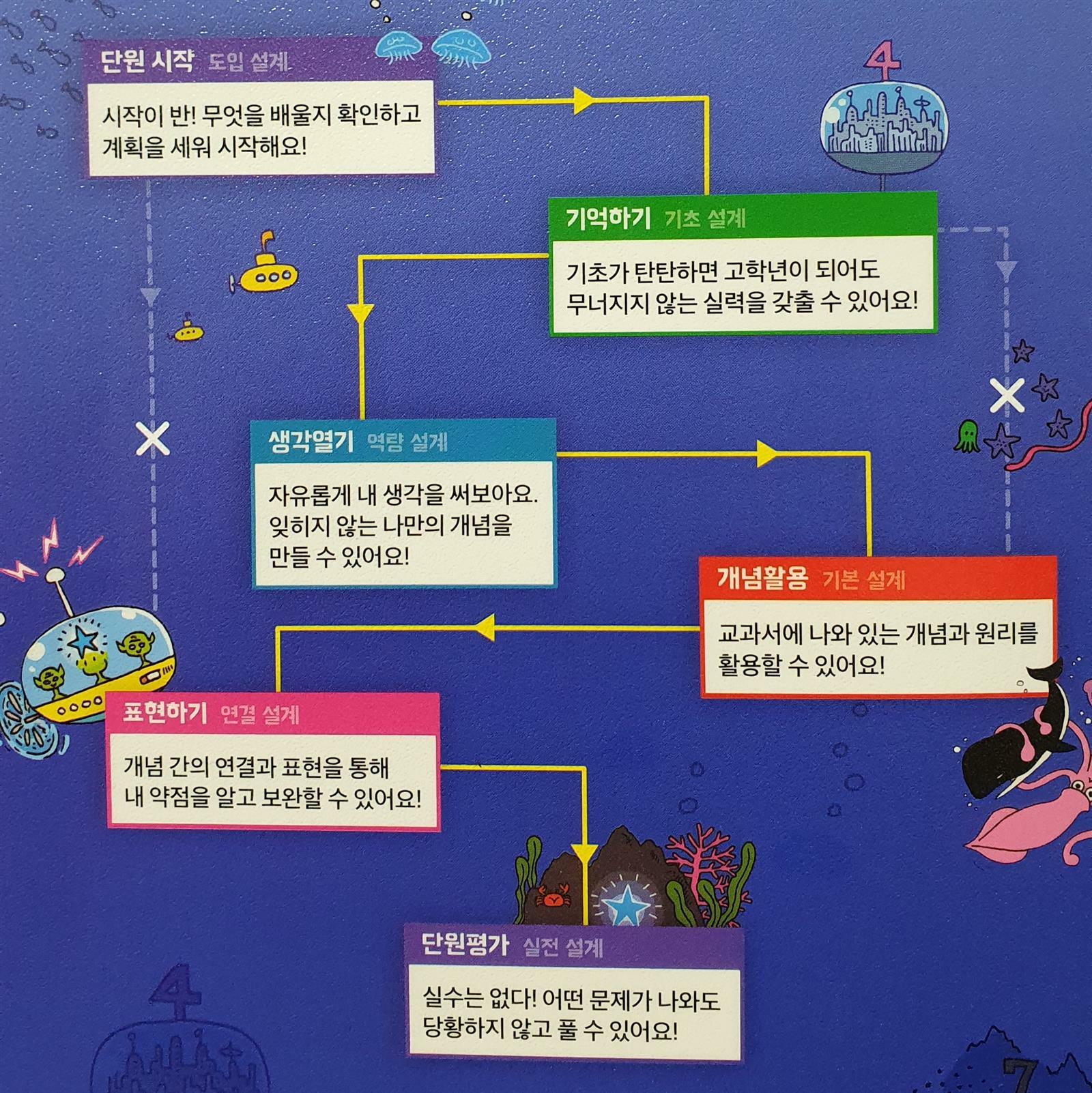
그래서 수학의 미래는

개념과 개념을 연결해 수학의 재미를 알려주는

6단계 학습을 적용하고 있어요.

① 단원시작 (도입 설계)

② 기억하기 (기초 설계)

③ 생각열기(역량 설계)

④ 개념활용 (기본 설계)

⑤ 표현하기 (연결 설계)

⑥ 단원평가 (실전 설계)

문제는 잘 풀어내지만

설명을 해보라 하면 어떻게 말해야 할지

모르겠다는 규씨와 『수학의 미래』

1단원부터 시작했어요.

세 자리의 수

2학년 1학기 첫 단원은 세 자리의 수예요.

1학년 2학기 때 100까지 배웠고

이제 확장된 세 자리 수의 자릿값에 대해 배우게 돼요.

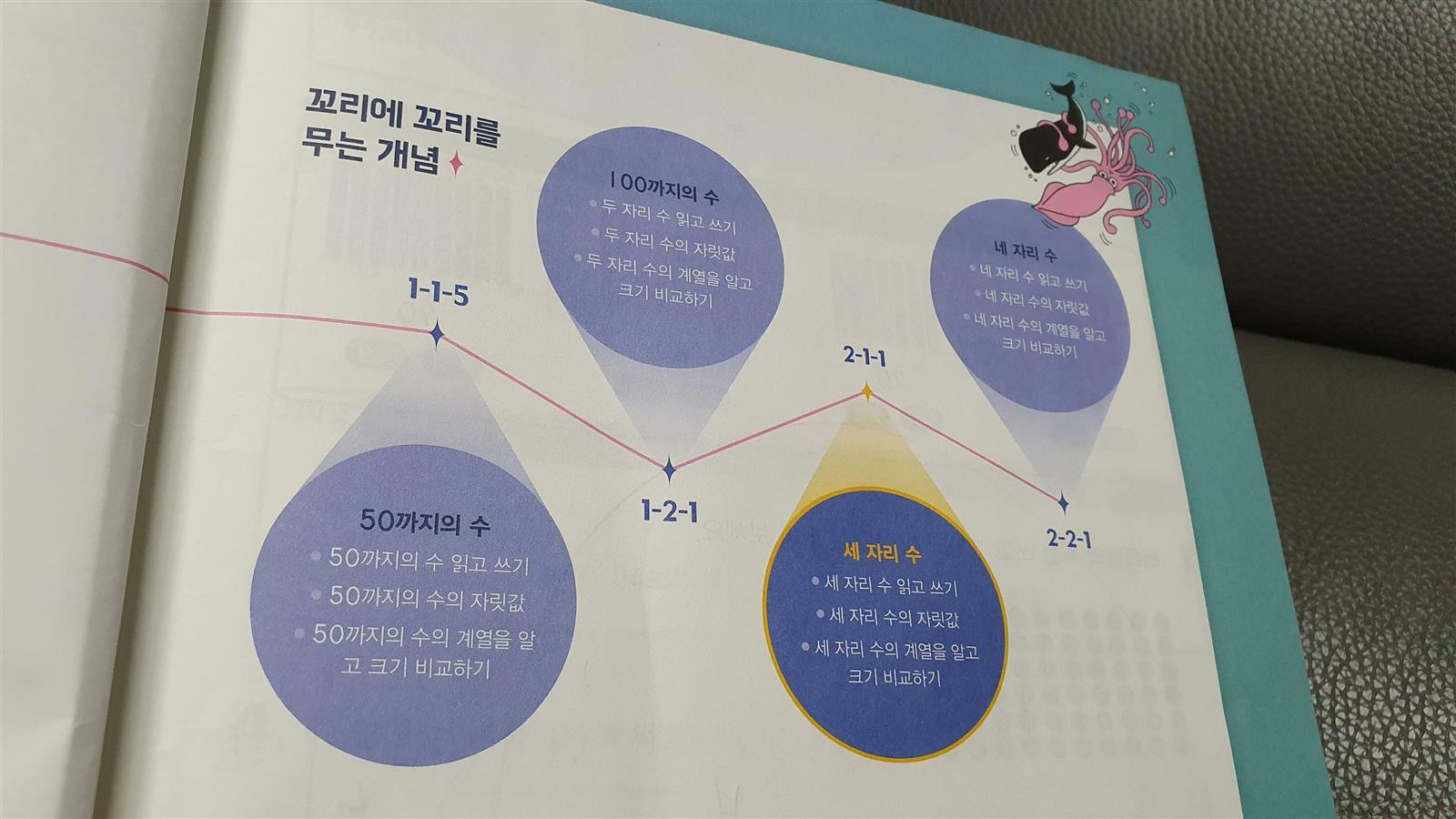
본격적인 풀이 전 <단원 시작>단계에선

1학년 1학기부터 배웠던 개념을

간략하게 소개해 놓았어요.

1학년 때 두 자리 수부터 배운 것을 확인하며

내가 왜 지금 세 자리를 배워야 하는지와

다음은 네 자리 수구나! 하는

배움의 흐름을 스스로 알 수 있게 해줘요.

▶ 말한 것, 생각한 것을 글로 꼭 써보세요.

▶정답만 쓰지 말고 이유도 꼭 써 보세요.

▶ 익숙하게 빨리 하는 것도 필요해요.

▶ 빨리 하는 것도 중요하지만,

자세하고 정확하게 하는 것이 더 중요해요.

이유나 풀이 과정을 써야 하는

서술형 문제가 많다 보니

스스로 다짐하기를 소리 내어 읽으며

시작하는 것도 좋더라고요.

수학의 미래 6단계 학습법이

실제로 적용된 문제집의 모습이에요.

<기억하기>에서 복습하고

<생각열기>와 <개념활용>을 통해

사고력과 개념정리로 기본기를 다진 뒤

<표현하기>와 <선생님 놀이>과정에서

배운 것을 정리해 서술하는 능력을 키우고,

마지막 <단원평가>에서 '기본'과 '심화'의

서로 다른 난이도 문제를 풀어보며

스스로 배운 것을 확인해

자기주도 학습을 완성하는 시스템인 거죠.

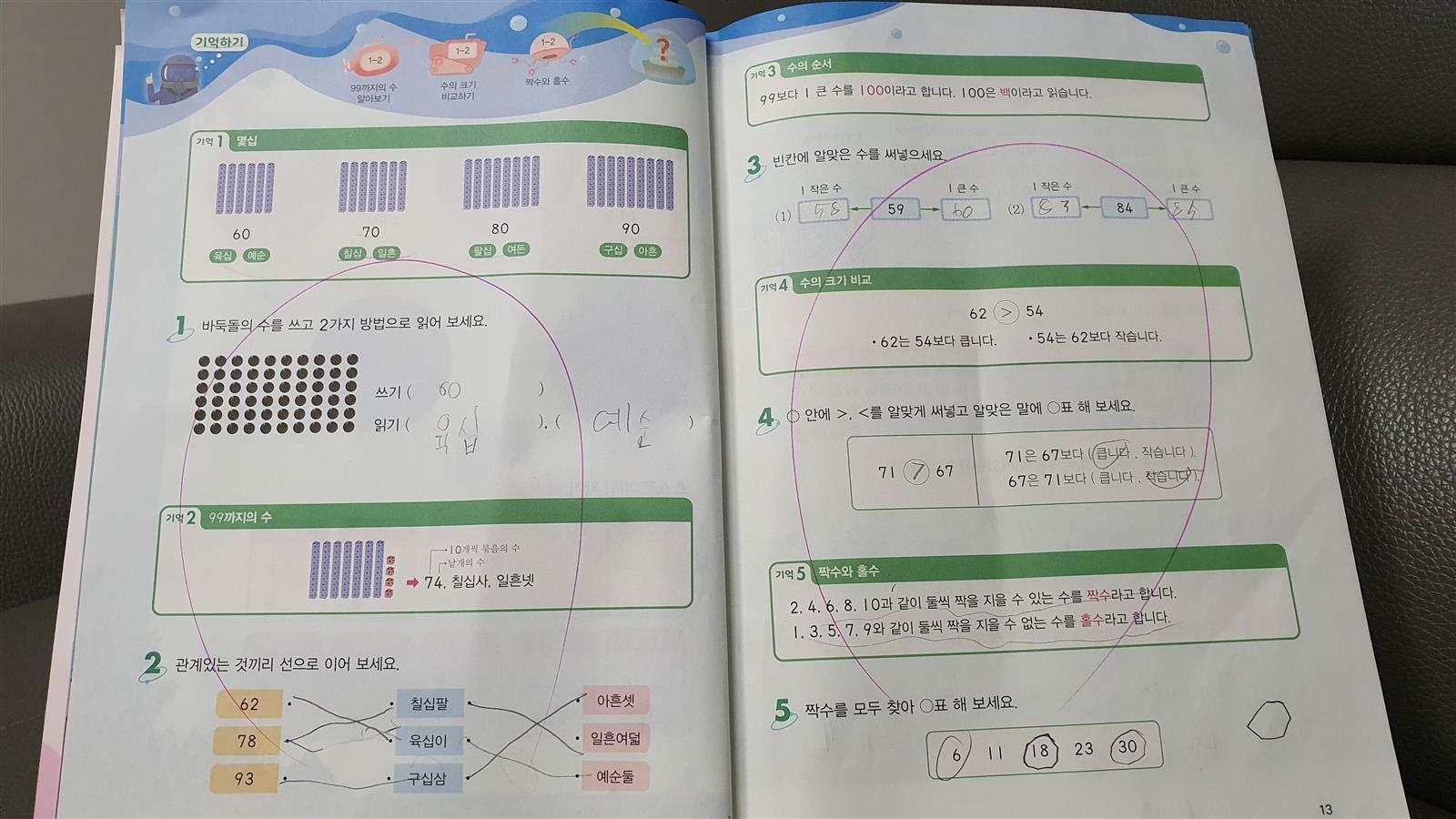
<기억하기>

1학년 2학기 수학의

기억을 되살려 복습에 들어갔어요.

수를 2가지 방법으로 읽는 문제들은

헷갈려 했었는데 이제 제법 풀어내는

단계가 되었어요.

99까지의 수, 수의 순서,

수의 크기 비교, 짝수와 홀수까지

열심히 해온 보람을 확인하는 순간이네요.

<생각열기 ①>

수학의 미래 첫 서술형 문제예요.

낱개의 구슬 100개를 세어보고

어떻게 세었는지 써보는 문제가 나왔어요.

규씨의 답을 살펴볼게요.

●●●

십이 다섯게가 있으니까 50이고

또 십이 다섯게가 있스니까 100개 있습니다.

또 다른 방법으로 세어보자.

세로로 5, 10, 15처럼

5씩 커지게 할 수도 있습니다.

●●●

가로로 10개씩 묶어서도 세어보고

세로로 5개씩 묶어서도 세어본 뒤

생각을 정리해서 잘 써 내려갔어요.

책의 뒤쪽에 첨부되어 있는

정답과 해설지를 보며 예시 답들도 살펴봤어요.

1개씩 이어 세는 방법도 적어볼 수 있었네요.

10개씩 뛰어 세기 한 것과

10씩 10묶음으로 센 것의 표현들도

규씨와 함께 보며 수학적 표현 방법들도

다시 체크해봤어요.

<개념활용 ①-1>

100 알아보기를 통해 90보다 10 큰 수 100과

수 모형으로 100의 자릿수도 개념을

다시 익힐 수 있었어요.

<생각열기 ②>

학생들이 만든 팔찌 100개들이 2상자의

그림을 보고 어떻게 세었는지 써보는 문제가 나왔어요.

●●●

10, 20, 30처럼 10씩 셌습니다.

●●●

이 문제는 다시 써 볼 필요가 있었어요.

세 자리 수를 알아보기 전

100개씩 세어보는 문제였기에

10개씩의 수 모형 문제와 100개 들이 1상자의

차이에 대해 이야기를 나눈 뒤 수정했어요.

●●●

10, 20, 30처럼 10씩 셌습니다.

↓

100+100=200처럼

100을 두 번 셌습니다.

●●●

고쳐 쓴 답을 보니

100씩 뛰어 세는 문제에 대해

이해한 게 느껴졌어요.

이 문제 역시 수정의 단계를 거친 뒤

정답과 해설을 보고 다양하게 세는 방법을

같이 확인했어요.

저도 규씨도 『수학의 미래』 문제집에

적응되어가고 있었어요. 훗훗

"나에게 필요한 '진짜 수학'

스스로 모험하고 발견하다!"

전 이 모험이란 단어가 와닿더라고요.

처음 보는 2학년 문제를

아무런 설명 강의도 없이 풀려도 되는 걸까?

은근한 불안심리가 있었던 터였거든요.

<생각 열기>로 처음 접하는 개념에

부딪혀보고 실패도 하며 대체 이게 뭐지?

궁금해하며 스스로의 힘으로

개념 근처에 다가간 뒤 <개념활용>을 통해

앞에서 궁금했던 부분을 해소하다 보면

자기주도적인 학습 습관이 형성될 수 있겠어요.

기계적으로 연산 문제의 정답만 찾는 것이 아니라

개념을 알아차리고 직접 설명할 수 있도록

도와주는 『수학의 미래』

꼬마 수학 선생님이 되는 그날까지

천천히 차분하게 풀어보자~

============================
■ 출판사로부터 도서 협찬을 받고
본인의 주관적 견해에 의해 작성하였습니다. ■
============================