-

-
최상위 쎈 초등 수학 3-1 (2019년용) ㅣ 초등 최상위 쎈 (2019년)
홍범준.신사고수학콘텐츠연구회 지음 / 좋은책신사고 / 2017년 11월
평점 :

구판절판

안녕하세요~
드디어 아이들의 개학이 4일 앞으로 다가왔습니다.
정말 길고 긴 방학이었어요.^^
초등 3학년이 되는 아이와 최상위쎈을 풀어보고 있는데
우공비 수학보다는 난이도가 있는 수학교재인듯합니다.
수포자 만들지 않기위해 열심히 하루에 한페이지씩~ 꾸준히 풀어주고 있지요.

좋은책 신사고 최상위쎈 초등수학3-1
심화부터 경시까지 고난도 문제 총망라.
심화유형 집중학습 시스템으로 문제해결력 업그레이드.
3단계 난이도별 학습으로 고난도 문제 완전 정복.

최상위쎈 수학도 역시나 신사고 무료 모바일 러닝으로
문제풀이 동영상 강의를 들을수 있답니다.
아이 혼자서 풀다가 막힐때는 역시 동영상 강의가 답이죠!

한차원 높은 최상위 수학의 시작과 끝!
개념학습 - 문제학습 - 실전학습 - 자기주도학습
단원별로 교과 내용을 빠짐없이 정리하여 고난도 문제를 풀 때 유용한 개념 및
방법을 정리해 두었습니다.
알파단계에서는 시험에 자주 출제되는 고난도 문제를 유형화하여
단계별 문제로 제공하고
유제를 통해 유형을 다질수 있게 하였으며,베타단계는 심화개념과 심화유형을
종합적으로 학습할수 있는 단계로 신유형, 통합형 문제를 제공하고 있습니다.
감마단계는 최고난도 문제를 통해 종합적 사고력과 응용력을 기를 수 있는
단계로 제공된 QR코드를 스마트폰에 인식시키면 최고의 선생님이
직접 강의하시는 문제 동영상을 무료로 학습할수 있습니다.

차례 덧셈과 뺄셈, 평면도형, 나눗셈, 곱셈
길이와 시간, 분수와소수.
그동안 해왔던 문제들인데 평면도형과 분수와 소수는 낯선 단어.
뭐 꾸준히 하면 되니까 걱정은 없네요.^^

1단원 덧셈과 뺄셈 단계는
개념학습, 알파단계, 베타단계, 감마단계로 나뉘어 집니다.
잘했으면 웃는얼굴, 부족하면 시무룩?한 얼굴...........

1.처음에는 세자리수의 덧셈입니다.
받아올림이 없는 덧셈, 받아올림이 한 번 있는 덧셈
받아올림이 두번 있는 덧셈, 받아올림이 세번 있는 덧셈.
2.두 수의 합이 가장 크거나 가장 작은 덧셈식
서로 다른 세수가 주어졌을때
두 수의 합이 가장 큰 덧셈식은 ▷가장 큰 수 + 두 번째로 큰수
두 수의 합이 가장 작은 덧셈식은 ▶가장 작은 수 + 두 번째로 작은 수

3.세 자리 수의 뺄셈
받아내림이 없는 뺄셈
받아내림이 한번 있는 뺄셈-십의자리에서 받아내림이 있는 뺄셈
백의 자리에서 받아내림이 있는 뺄셈
받아내림이 두번 있는 뺄셈.
4.두 수의 차가 가장 크거나 가장 작은 뺄셈식
서로 다른 세 수가 주어졌을 때
두 수의 차가 가장 큰 뺄셈식 ▷가장 큰수 -가장 작은 수
두 수의 차가 가장 작은 뺄셈식 ▶주어진 수들을 두 개씩 짝지어 차를
모두 구하여 알아보기
(주의) 두 수의 차가 가장 작은 뺄셈식을 두 번째로 작은 수 -가장 작은 수로
생각하지 않도록 주의하기!

어림하여 계산하기
ex)251+127에서 251은 250
127은 130으로 어림하여 계산할수 있습니다.
250+130=280
ex)859-327에서 859는 860
327은 330으로 어림하여 계산할 수 있습니다.
860-330=530
*세 수의 뺄셈 또는 덧셈과 뺄셈이 섞여 있는 식은 앞에서부터
두 수씩 차례로 계산합니다.
ex)354+127-269일때
354+127=481
481-269=212
이렇게 차례대로 계산합니다.
기본적인 개념부터 다잡아주니 참 좋은것 같아요.
드디어 문제풀기 시작!

처음 푸는 문제라 아이는 기대반, 걱정반이었던것 같아요.
그런데 생각했던것보다는 쉬웠던지 자신있게 풀어주었습니다.

쉽게 풀어주다보니 간혹 실수를 하네요.
식은 맞게 썼는데 답을 틀린거에요.
649+362=1011인데
1101이라고 써놓았네요.

계산결과가 가장 크게 되도록 식을 만들어 보는 문제가 나왔습니다.
덧셈식에서는 가장 큰수와 두 번째로 작은 수를 더하면되지만
뺄셈식이 있는 문제를 풀때는 더 집중해서 풀어줘야 한답니다.
ex)843, 561, 674, 729라는 숫자가 주어졌다고 할때
( )-( )+( )라는 식을 만족하는 식을 완성해보기.
세 수를 사용해야 한다고 할때 필요없는 수는 674.
729-561+843 =1011

발전5-2) 어떤 세 자리 수의 일의 자리 숫자와 백의 자리 숫자를 서로 바꾼 후
157을 더해야 할 것을 잘못하여 일의 자리 숫자와 십의 자리 숫자를
서로 바꾼 후 157을 더했더니 721이 되었습니다.
바르게 계산한 값을 구하시오.
앞서 푼 문제들과 비슷한 유형인데 감을 못잡은 문제예요.
( )+157=721
( )=721-157
( )=564
어떤 세 자리수는 546.
바르게 계산한 값은 546의 일의자리 숫자와 백의자리 숫자를 서로 바꾼 수
645에 157을 더해야 하므로
645+157=802입니다.
이런 유형의 문제는 잘 틀릴수 있을것 같아 더 많이 풀어보는게
좋을것 같아요.

합 또는 차를 이용해 두 수 구하기 문제입니다.
세 자리 수 61㉠과 ㉡98의 두 수의 합이 917일때 두 수의 차를 구하기.
61㉠+㉡98=917
㉠=9
㉡=2
619-298=321
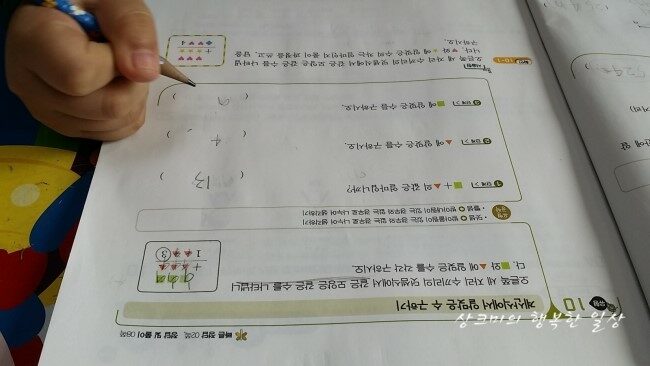
계산식에서 알맞은 수 구하기입니다.
숫자 대신 모양으로 알아맞추기!
같은 모양은 같은 수를 나타낸다고 할때 알맞은 수를 구하기.
□□□+△△△=1△△3
덧셈식일때 받아올림이 있는 경우, 없는 경우로 나누어 생각하기.
위와 같은 경우는 받아올림이 있는 경우인게 확연히 보이네요.
그렇다면 □과 △의 숫자는 반올림이 되는 숫자여야 한다는 점이에요.
□+△=3, □+△=13
그렇게 풀어주니 □=9
△=4가 되겠네요.

최상위쎈 수학 3-1 베타 문제 들어갔어요.
최상위쎈은 좀 더 난이도가 있는 문제더라구요.
더 많은 사고를 하게 만드는 수학교재!!
한권 풀고 나면 다른 문제들 푸는게 더 수월해질것 같아요.
아이 문제 푸는것 도와주면서 엄마도 공부하게 되는것 같기도 하고요.
욕심부리지 않고 조금씩 차근차근 문제풀거랍니다.
사고좀 한다는 친구들은 최상위쎈 수학 만나보세요!^^