-

-
숨마쿰라우데 중학수학 개념기본서 3-하 (2026년용) - 2015 개정 교육과정 ㅣ 중등 숨마 수학 (2026년)
강순모 외 지음 / 이룸이앤비 / 2019년 10월
평점 :




벌써 중3!
아직 1학기 수학 예습도 못 마쳤지만
3학년 2학기 스타트업 시작도 했고
겨울방학 동안 중3 수학 예습에
집중하려고 해요.
그래서 지금부터 3학년 2학기
개념 기본서로
3학년 2학기 수학 예습 신청합니다.

3학년 2학기에는
삼각비, 원의 성질,
통계를 공부할 거예요.
2학년 2학기 수학 공부가
거의 다 끝나가는 지금이
예습 시작하기에 딱 알맞은 시기네요.


3학년 2학기에는 총 61개의 핵심 개념을 공부하네요.
학습 분량이 적은 건지...
더 어려운 개념인 건지...
전 학기보다 핵심 개념이 적어요.
교재도 1학기나
2학년 2학기에 비해 얇고요...
어렵던지... 적던지...
숨마쿰라우데 중학 수학 개념 기본서로
공부하다 보면
얼마든지 잘 배워 나갈 거란 생각이 듭니다.

삼각비 단원에서는
1. 삼각비
2. 삼각비의 활용을 공부할 거예요.
아름다운 스웨덴의 스톡홀름 사진이
어려운 수학 공부에 대한 생각을
확 트이게 해 주네요
개념 기본서 공부하면서
저희 아이도 수학이 개념이
이렇게 탁 트였으면 좋겠습니다.


삼각법과 천문학의 관계는
그리스 시대부터 시작되었대요.
그리스 사람들이 바다 건너 여행할 때
하늘의 별자리를 길잡이 삼아 다녔는데
하늘의 반구 형태의 면으로
구면상에서 도형을 연구했고
오늘날 구면삼각법이라는
수학 지식을 얻게 되었대요.
그리스의 학자 히파르코스는
천문학을 연구하던 중 지구와 달의 거리를
계산하기 위해 삼각법의 연구하였고,
삼각법의 아버지라고 부르곤 한대요.
이를 인도의 수학자 일콰리즈미가 사인표를 만들고,
하바시 알하시브가 탄젠트표를 만들고
독일의 수학자 레기오몬타누스가
삼각법을 천문학과 분리하여 소개하였대요.
이후 sin, cos, tan 등과 같은 기호를
체계화되면서 발전해 왔대요.
삼각법을 그냥 공부하는 것보다
이렇게 삼각비의 역사를 알고 공부하려니
뭔가 제대로 알 것 같은 느낌이 듭니다~^^

맨 처음 배우는 핵심 개념은 삼각비에요.
먼저 도형의 닮음과 피타고라스의 정리를
알고 있는지 확인부터 하고~~~
삼각비란?
직각삼각형에서 두 변의 길이의 비를 말해요.
닮은 삼각형은 대응변 사이의 길이의 비는
각각 일정해요.
그래서 한 예각의 크기가 정해지면
직각삼각형의 크기에 상관없이
직각삼각형의 두 변의 길이의 비는 항상 일정해요.
각각의 기호를
sin, cos, tan로 표현해요.

사인은 빗변의 길이에 대한 높이이고
코사인은 빗변의 길이에 대한 밑변의 길이,
탄젠트는 밑변의 길이에 대한 높이에요.
그림을 보면서 알아가면
이해가 더 쉬워요.
예제 문제까지 풀면 삼각비는 완성~^^
핵심 개념 2는
'직각삼각형에는 삼각비를 이용하여
변의 길이를 구할 수 있을까?'에요
별이 2개인 건 그만큼 중요하다는 거니깐
정확히 이해하도록 노력해야 해요.
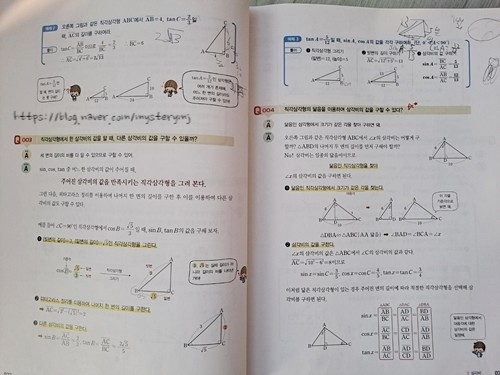

3번째 핵심 개념!!
'직각삼각형에서 한 삼각비의 값을 알 때,
다른 삼각비의 값을 구할 수 있을까?'
답은 구할 수 있다네요.^^
개념 기본서는 구할 수 있음을
충분히 이해할 수 있도록 증명해 주고,
예제 문제를 풀면서 완벽하게 습득하도록 해 주네요.
4번째 핵심 개념
'직각삼각형의 닮음을 이용하여
삼각비의 값을 구할 수 있다?'
답은 구할 수 있다에요.
닮음인 직각삼각형에서 크기가 같은 각을
구하면 돼요.

5번째 핵심 개념!!
'직선이 x축과 이루는 예각의 크기가 θ일 때
sin θ의 값은?'
원점을 꼭짓점으로 하는
직각삼각형을 찾아 변의 길이를 구하면 돼요.
6번째 핵심 개념
'입체도형에서 삼각비의 값을 어떻게 구할까?'
직각삼각형을 찾으면 OK에요.

개념을 이해했는지 확인하는
개념 CHECK 문제들~
이 단원에서 배운 용어와 학습원리를 점검하고
개념 문제들을 풀어요.
개념 문제들을 잘 풀었다면 진도를 계속 나가고,
혹시 틀린 문제가 있다면
앞의 핵심 개념으로 돌아가서
복습을 하면 되겠죠?^^

삼각비가 무엇인지 공부한 후에
이제부터는 삼각비의 값을 공부합니다.
9개의 핵심 개념을 질문하고
답을 찾아가고
예제 문제를 풀면서
개념에 대한 완벽 이해를 합니다.
뭔가 복잡해 보이는 표와 그림이
어려워 보이지만
개념 기본서를 하나하나 따라가다 보면
어느새 예제 문제도 쉽게 풀고 있어요.
예제 문제도 문제 풀이에 목적을 두지 않고
개념 이해에 그 목적을 두고 있어서
답을 찾기보다는
왜 이렇게 풀어내는지 이해하는 게 좋아요.

소단원별로 개념 CHECK 문제를 통해
내가 개념을 얼마나 정확히 이해했는지
점검하는 시간이에요.
문제풀이를 통해 개념을 완벽히 이해하는 시간을 가져요.

소단원별로 시험에 반드시 나오는 유형들을
모아 정리해 놓은 유형 EXERCISE!!!
유형별로 나누어져 있어서
풀기에도 좋고
시험에 잘 나오는 문제들이라
학교 시험에 대비하기도 좋아요.
이렇게 숨마쿰라우데 중학 수학 개념 기본서로
공부를 해온 덕분에
이번 기말고사도 만점을 받았나 봐요.
앞으로도 유형 EXERCISE 문제부터
꼼꼼히 풀어야겠어요.

스스로 문제를 파악하여 해결하며
실력을 완성하는
중단원 EXERCISE!!
앞에서 유형 문제들을
완벽히 이해했다면
전혀 어렵지 않게 풀 수 있는 문제들이에요.
중단원 문제들까지 해결한다면
학교 시험 만점은 걱정 없겠네요^^

각 소단원들을 공부한 후에는
대단원 REVIEW로 마무리해요.
각 핵심 개념의 질문에
간단, 명료하게 답을 해 놨어요.
질문에 대한 답을 스스로 하면 더욱 좋고
REVIEW를 읽으면서
개념을 정리하는 시간을 가져도 좋아요.

드디어 삼각비 단원을 완전히 마무리하는
대단원 EXERCISE 시간~!!!
각 문제마다 난이도도 표시되어 있고
서술형 문제도 3문제나 있어요.
어서 대단원 문제까지 풀어서
삼각비를 얼마나 잘 이해했는지 알고 싶네요.
이번 겨울방학을 이용해서
숨마쿰라우데 중학 수학 개념 기본서로
3학년 수학도 쉽게 공부하고 싶습니다~