-

-
수학 개념 따라잡기 : 확률의 핵심 - 지식 제로에서 시작하는 ㅣ 지식 제로에서 시작하는 개념 따라잡기 시리즈
Newton Press 지음, 이선주 옮김, 곤노 노리오 감수 / 청어람e(청어람미디어) / 2020년 11월
평점 :



확률 개념을 ~~
다양하고 재미난 사례를 통해서 알려주는 책이 다 있네욧! ^^
청어람미디어 출판사의
지식제로에서 시작하는 수학개념 따라잡기시리즈 중 하나인
< 확률의 핵심 >인데요!
확률이 뭔가 궁금해서 재미있게 접근 하고싶은 일반인이나
개념을 쉽게 이해하고싶은 중고청소년들에게 일독하기를 권하고 싶네요~~~ ^^
지식제로에서 시작하는 수학개념 따라잡기시리즈는
< 확률의 핵심 > 뿐 아니라 ~~~
미적분의 핵심, 삼각함수의 핵심, 통계의 핵심, 로그의 함수 등
다양하게 나와있어요!
< 확률의 핵심 > 은
과학잡지 Newton 을 발행하는 일본 출판사 Newton Press 에서
별책 < 확률에 강해진다 > 의 기사 일부를 발췌 및 대폭 추가 재편집을 해서
만든 책이라고 하네욧!
#확률의핵심

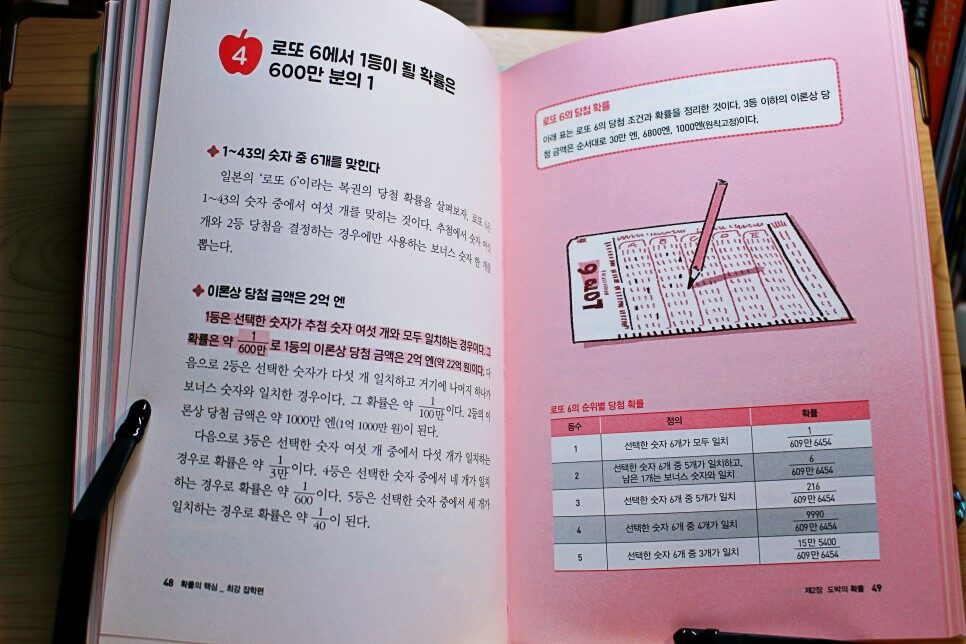
로또 1등 될 확률 즉,
추첨 숫자 6개와 모드 일치하는 경우는
600만 분의 1 이라고 하네욧! ㅠㅠㅠㅠ
더 정확하게는 609만 6454 분의 1 이라고 하니 !!!
당첨되는 분들은 정말 억겁의 행운아임에 틀림없는거 같네욧! ㅋ
그래도 벼락에 맞을 확률보다는 높다는 팩트!!! ㅋㅋㅋㅋ
미국에서 벼락에 맞을 확률은 122만2000 분의 1 이고
일본에서 벼락에 맞을 확률은 851만 3500 분의 1 이라고 함!
로또는 복잡해서 그런지 계산 공식이 없던데
벼락에 맞을 확률은 계산 공식이 나와있더라구요! ㅋ
10년동안 벼락,낙뢰로 사망/부상/행불 된 사람의 수를
현재 일본의 총인구수로 나눈 것이라 ~~
우리나라로 적용하면 수치가 좀 달라질 거 같네욧!
여튼 로또가 벼락에 맞을 확률보다는 높다고 하니 ㅋㅋㅋ
적은 돈으로 벼락부자가 될 꿈을 꾸며 한두어장 정도 재미로 사는 것도
나쁘진 않을 거 같아요!
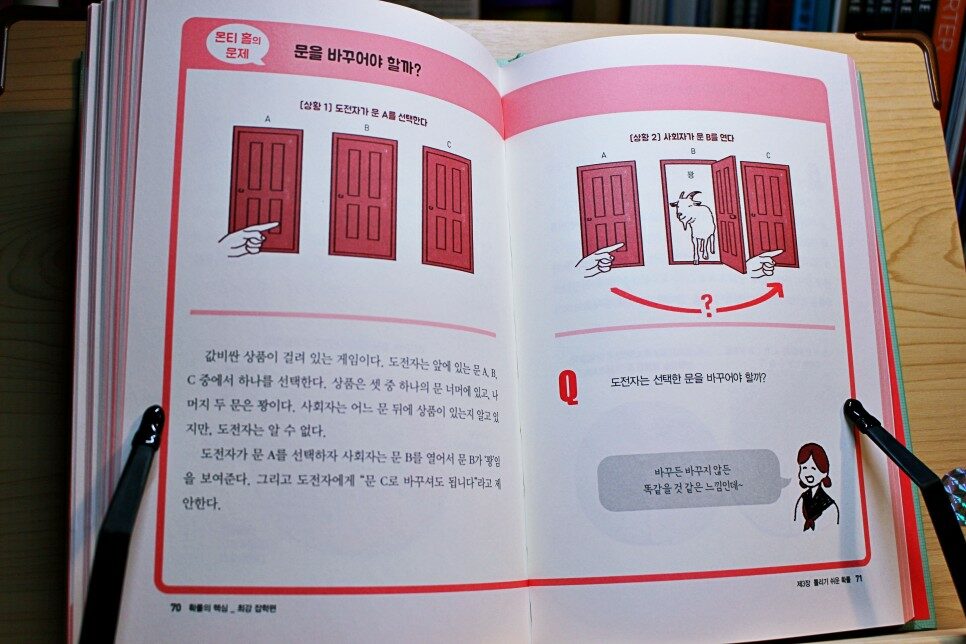
미국의 한 퀴즈 프로그램에서 나온 문제로
사회자의 이름을 따서
'몬티 홀의 문제'라고 하는
세계적으로 유명한 문제가 나왔네욧!
문 A, B, C 세개 중~~
문 한개 뒤에만 상품이 있고, 나머지 문 2개는 꽝~~~ ㅋㅋㅋ
도전자가 문 A를 선택하면 !
답을 알고있는 사회자는
문B를 열어서 문B가 꽝임을 보여주고
도전자에게 문 C 로 바꿔도 된다는 멘트를 날림!
그러니까 문A 또는 문C 뒤에는 반드시 상품이 있다는 거지요!
그렇다면 도전자는 선택한 문A 를 C 로 바꿔야 할까요???
역사상 가장 IQ 높은 여성으로 알려진
마릴린 사반트가
바꾸는 게 좋다고 확률이 1/3 에서 2/3 으로
증가한다고 답했는데요!
많은 수학자가 여기에 오류가 있다고 지적하는 등
논란이 계속되자
결국 학교수업 및 국립연구기관의 검증하게 되었는데
결과는 !!!
사반트의 말이 옳았다고 해요! ㅋ
역시 여자의 말이 옳다구요! ㅋㅋㅋㅋ
책에 상세한 해설이 있으니
관심있으신 잇님들은
어떻게 결과치가 도출되는지 한번 읽어보시는 것도 좋을 거 같네요~~
역사상 확률론에 관해 처음 책을 쓴 사람은
이탈리아 수학자 지롤라모 카르다노라고 하네욧!
의학으로 학위를 따고, 천문학,물리학,수학 등에도 정통한
완전 똑똑하신 분인데~~
어쩌다 도박에 심취하셨는지 ㅋㅋㅋ
< 주사위 놀이에 관하여 > 라는 논문을 썼다고 하네욧! ㅋㅋㅋ
이렇게 확률론의 발전에는 도박에 몰두하신 수학적 도박사들의 공적이 녹아들어있다고 하니 ~~~
도박이 나쁜 것만은 아닐수도 있겠다 싶더라구요! ㅋㅋㅋ

2부 <최강 교과편>에서는
확률이란 무엇일까( 수확적확률과 통계적 확률),
수확적 확률 계산 할 때 '경우의 수' 및
확률이 덧셈정리, 곱셈정리, 여사건으로 생각하기, 기댓값 구하기 등등
교과적인 내용도 알차게 들어있어요~~~
확률에 흥미가 없는 중고등 학생들에게도
재미있게 확률을 공부할 수 있도록 구성되어 있는 점이
중딩 딸래미가 있는 저에게
완전 맘에 드네요!! ^^
출판사로부터 책을 제공받아 주관적으로 작성한 글입니다.