파이썬을 활용한 베이지안 통계: 동전 던지기와 하키 승률로 배우는 데이터 분석 - 한빛미디어

파이썬 라이브러리를 활용한 데이터 분석 - 수정보완판, pandas, NumPy, IPython, matplotlib로 지진 데이터 시각화, 선거와 인구통계 분석 등 실사례 사용
웨스 맥키니 지음, 김영근 옮김 / 한빛미디어 / 2013년 10월

 

 

'베이지안으로 생각하고 프로그래밍하라'라는 메시지를 보고 심리학적 접근 방식에서 많이 인용될 것 같은 생각이 들어 인터넷에서 찾아보니 심리학에서 인간의 사고 과정을 베이지안 관점에서 풀어나가는 내용들을 많이 확인 할 수 있었다. 그리고 빈도주의와 베이지안 학파간의 논쟁 또한 베이지안을 공부하기 전에 한번씩 찾아 보면 이 책을 읽는데 있어서 즐거운 책읽기가 될 것 같다. 

책의 앞부분에서는 베이즈 정리에 대한 이론 설명을 한다. 이 부분은 뒤의 실제 파이썬 프로그래밍을 하는데 있어, 기본이되는 이론이기에 반드시 이해해야 한다.

특히 조건부 확률과 결합 확률을 통해 베이즈 이론을 이끌어 낸다. 그 다음장에서는 파이썬 모듈을 통해 베이즈 이론 사용법(계산 통계)을 보여준다. 후반부에서는 추정, 공산과 가산, 의사 결정 분석, 예측, 관측 편향, 두 차원, 근사 베이지안, 가설 검증, 증거, 시뮬레이션, 계층 모델, 차원 다루기 등의 냉용이 이어진다.

아래는 베이즈 이론을 정리한 내용이다.

사후확률은 사전확률과 가능도의 곱에 비례한다.

 

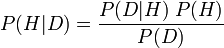
여기서

• 는 가설이다. 는 데이터이다.
•  는 의 사전 확률이다. 즉 가 보이기 전까지는 가 참일 확률이다.
• 는 를 보게 됨으로써 가지는 가 참이 되는 조건부 확률이다. 가능도(Likelihood)이다.
• 는 의 경계 확률이다.
• 는 사후 확률이다. 이 확률은 주어진 데이터와 가설에 대한 사전 믿음이 주어진 상태에서 가설이 참일 때의 확률이다.

이 이론을 설명하면서 몇 가지 재미있는 사례에 대한 설명이 있다.

쿠키 꺼내기 문제, M&M 초콜릿 문제, 몬티 홀(TV 게임 쇼) 문제, 주사위 문제, 기관차 문제, 유로 문제, 보스턴 브루인스 문제, 레드라인 문제, 페인트볼 게임, 신장 종양 문제, 가이거 계수기 문제, 하키 승률 등 실 생활에서 일어나는 문제에 대한 사례를 들어가며 문제를 재미있게(?) 풀어간다. 

​

책을 읽으면서 이론 하나하나를 모두 이해하기는 쉽지 않지만 (화두는 있는니 구글신에게 도움을 받으면 된다.) , 최소한 베이즈 정리에 대한 풀이를 파이썬을 통해서 배울 수 있다는 것만 해도 많은 도움이 될 것이다. 그리고 파이썬 베이즈 모듈을 활용하여 나만의 통계 모듈로도 훌륭한 도움을 얻을 수 있을 것이다. 가령 사내에서 제비뽑기시나 사다리를 탈때 어떤 선택을 하면 좋을지 등등을 베이즈 정리를 이용해 보는게 어떨까?ㅎㅎ 

통계를 공부하는 분들은 필독서로 권하고 싶고 꼭 프로그래머가 아니더라도 기획 또는 마케팅을 담당하는 분들에게도 한번쯤 보기를 권한다. 

소장 가치가 있어 내 서재에 꼽아 두고 읽을 것이다. (인간 심리학 측면에서도 도움이 될 것듯..ㅎ)