-

-
디딤돌 중학연산 3-1 B ㅣ 디딤돌 중학연산
디딤돌 수학연구회 지음 / 디딤돌 / 2020년 1월
평점 :

구판절판


디딤돌 / 중학 연산 3-1B
출간된 지 얼마 되지 않은 따끈따근한 교재!!
3-1A 교재가 너무 괜찮아 한 권 완북하고
눈빠지게 기다려서 드디어 받게 된 교재
디딤돌 중학 연산 3-1B!!

디딤돌 중학연산은 중학교 1학기 과정을
A, B 두 단계로 나뉘어 출간했는데요~
큰아이는 진작 인강으로 공부 중이라 따로 사용하는 교재들이 있어
초등 고학년이 되는 작은 아이가 먼저 디딤돌 교재를 접해보았거든요.
뭐 둘째에게 말할 것도 없지만
완전 딱!!!
이건 바로 우리 첫째를 위한 교재다 라고 올레를 외쳤답니다.
올해 3학년이 되는 1호군^^
사실 1학기 과정은 기본에서 유형까지 끝낸 상황이었고
현재 2학기 과정과 고등과정까지 천천히 선행 중이거든요.
수학 머리가 그다지 있는 아이가 아니라 사실
이 교재 저 교재 닥치는 대로
쩜 풀리게 하는 편인데 그렇게 실수가 많이 나옵디다.
개념이 확실하지 않아서 일까?? 돌아서면 또 실수 연발..
3학년 1학기과정 심화를 해야 하는 상황에서
역으로 돌아가 개념부터 다진다 생각하고
다시 복습 겸해서 디딤돌 중학 연산 3-1A는 겨울방학 동안 한 권 완북했고
3주간의 봄방학 동안 3-1B 완북을 계획하고 열심히 달리고 있답니다.
중학연산 3-1A 바로가기
▼▼▼▼
https://blog.naver.com/yiya3531/221786008194


디딤돌 중학연산은 위에서 잠시 언급했었지만
중학교 1학기 과정을 A, B로 나누어 구성했는데요
저희 1호군은 현재 3학년 1학기 과정인 3-1A는 완북하고
3-1B를 열심히 활용 중에 있답니다.


중학 연산 3-1A 과정은
중학교 3학년 1학기 과정 중에서도
실수와 그 연산과 식의 계산에 대한 내용으로
크게 두 개의 대단원 속에 8개의 중단원으로 다시 나뉘어 구성하였고요


중학 연산 3-1B는
크게 이차방정식과 이차함수 두 개의 대단원 속에
6개의 중단원으로 나뉘어 구성되어 있습니다.

중3쯤 되면 이제 주도 학습은 당연한 말 맞는 거죠??
근데 그건 다른 애들 얘기고요~ㅠ
아직까지 스스로 학습이 힘든 저희 집 1호 군입니다.
사실 참 이런 말 하기가 부끄럽긴 한데
아직도 해라해라 잔소리와 함께 분량까지 체크해주는 걸 좋아합니다.ㅠ
그래서 하루에 얼마큼 해야 한다는
"학습 계획표"가 저희 집에선 아주 유용하게 쓰이고 있답니다.
현재론 중단원 한 개를 일주일 분량으로 잡고
나름 계획적으로 열심히 하고 있답니다.



디딤돌 중학연산은 보는 즐거움이 있습니다.
핵심 개념과 연산 속 개념, 그리고 수학적 개념이
이미지로 빠르고 쉽게 이해되고 오~~래 기억될 수 있도록 한답니다.

디딤돌 중학연산은 문제를 푸는 즐거움이 있습니다.
학생들에게 가장 필요한 개념을
충분한 문항과 촘촘한 단계별 구성으로
자연스럽게 이해하고 적용할 수 있게 합니다.

디딤돌 중학연산은 개념을 발견하는 즐거움이 있습니다.
생각을 자극하는 질문들과 추론을 통해 개념을 발견하고
개념을 연결하여 통합적 사고를 할 수 있게 한답니다.
눈으로, 손으로, 머리로 개념이 발견되는 중학 연산!!
직접 풀어보면서 한번 느껴볼까요??

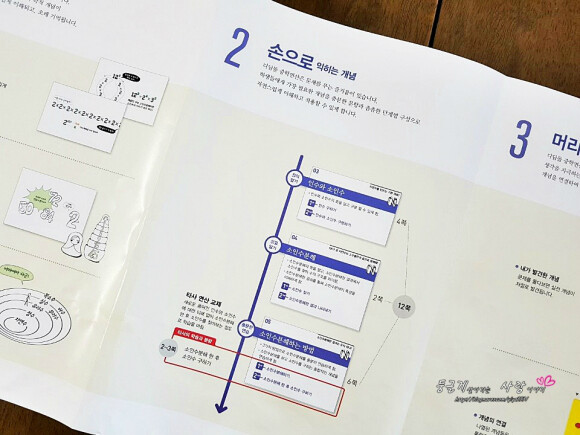
2단원은 이차방정식의 근의 공식에 대한 내용으로 공부하게 되는데요
각 단원에서 배우게 될 전체적인 개념들을 이미지화해서
전체적으로 한눈에 보기 쉽게 쉽게 정리해 두었답니다.
우선 본격적으로 2단원에 들어가기 앞서 개념만 한번 쫙~~~
정독하면서 훑어보게 하고요~
본격적인 개념은 문제를 풀어보면서 쩜 더 자세히 살펴보도록 합니다.

01. 이차방정식의 근의 공식 (1)
< 근의 공식으로 x를 찾아라! >
이번 시간부터 본격적으로
이차방정식의 근의 공식을 이용해서 문제를 풀게 되는데요
우선 개념 설명에서 근의 공식이 유도되는 과정을 잘 설명해주고 있답니다.
물론 근의 공식만 외워서 문제를 푸는 것도 중요하지만
완전제곱 꼴로 바꾸어 식의 변형을 거치게 되는데요
단순히 공식만 외우기보다는
이런 식의 변형 자체를 꼭 알고 있어야 하는 것도
중요한 공부 과정 중 하나겠지요.
자~ 이제 근의 공식만 머리에 쏙 넣어 두면
아주 간단히 이차방정식을 풀어낼 수 있답니다.

" 근의 공식을 이용해서
계수만 넣어주면 답이 나온다!! "
이차방정식의 근의 공식을 적용하면서 문제 하나하나 풀어보면서
머릿속에 쏙쏙 넣도록 합니다.
오답없이 시작이 좋습니다.^^
02. 이차방정식의 근의 공식(2)
<근의 공식으로 x를 찾아라! >
이번 시간엔 이차방정식의 근의 공식으로 해를 구하되
일차항인 x의 계수가 짝수일 때
좀 더 쉽게 구할 수 있는 근의 공식이 있는데요
그것을 유도하는 과정을 잘 설명해 주고 있답니다.
역시나 근의 공식만 주야장천 외우는 것보다
근의 공식이 나오는 과정도 중요한 수학 공부이니
꼭 알고 넘어갈 수 있도록 합니다.
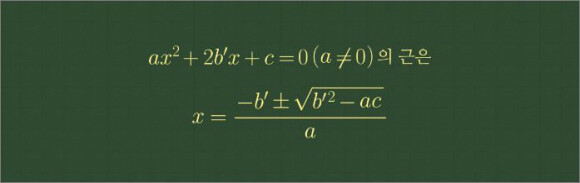
x의 계수가 짝수일 때의 근의 공식!!
일명 짝수 근의 공식도 잘 적용하면서
한문제 한문제 너무 잘 풀어주었습니다.

03. 복잡한 이차방정식의 풀이
< 계수를 정수로, x를 찾아라! >

복잡한 이차방정식의 풀이 방법에 대해 알아보았는데요
괄호가 있는 경우엔 괄호를 풀고 우변을 모두 좌변으로 이항한 후 구하고
계수가 분수일 경우나 소수일 경우
분수일 때는 양변에 분모의 최소공배수를 곱해 계수를 정수로 고치고
소수일 경우엔 양변에 10,100.... 을 곱해서 계수를 정수로 고친 후
ax²+bx+c=0의 꼴로 정리한 후 해를 구하면 된답니다.
구구절절 설명이 길긴 하지만
직접 풀어보면서 스스로 공식을 외우는 게
가장 정확한 방법이 아닐까 싶네요^^

04. 공통인 식이 있는 이차방정식의 풀이
< 공통부분을 치환! x를 찾아라! >

전체적인 풀이 과정을 단순히 위에 적힌 제 글만 봐서 어떠세요??
한눈에 딱 감이 오시나요??
네~~ 사실 저도 열심히 과정을 글로써 적고는 있지만
사실 뭔 말인지 다시 한번 읽고 읽고 해야 하겠더라고요.


구구절절 긴~ 설명은
NO! NO!
한눈에 쉽게 파악이 되는
디딤돌 중학연산은
전체적인 풀이 과정을 이미지화 계산 방법으로 설명해주고 있어
천천히 그 과정을 보고 있음
절로 아~~~하면서 고개가 끄덕여진답니다.
05. 이차방정식의 근의 개수
< √ 안의 부호가 근의 개수를 결정해! >
이차방정식 ax²+bx+c=0의 근의 개수는
근의 공식 √ 안의 b²-4ac의 부호로 알 수 있답니다.
① b²-4ac > 0 이면 서로 다른 두 근을 갖는다.
② b²-4ac = 0 이면 한 개의 근(중근)을 갖는다.
③ b²-4ac < 0 이면 근이 없다.
문제를 풀다 보면 위와 같이 중간중간 "내가 발견한 개념"이라는
노란 박스를 볼 수 있는데요
네모 빈칸을 채워가며 다시 한번 개념 정리를 통해
확실히 자기 것 정리해 볼 수 있는 코너랍니다.
이차방정식의 근의 개수를
내가 발견한 개념에서 다시 한번 정리해주고 있는데요
b²-4ac 가 0보다 클 경우엔 근이 2개
b²-4ac 가 0 일 때는 근이 1개
b²-4ac 이 0보다 작으면 근이 없다는 것을
다시 한번 빈칸을 채워가며 개념을 정리하면서 내 것으로 만들었답니다.

제 속 노~~란 박스가 눈의 확 띄나요?
수학적 개념과 법칙을 직관적으로 이해할 수 있게 했고
개념의 단원 안에서의 연계와 나열된 개념들을 서로 연결하고
이전에 배운 개념과 지금 배우는 개념 또는 앞으로 배울 개념들과 연결하여
통합적으로 사고할 수 있도록 구성했어요^^
노란 박스에 핵심 개념들만 짧고 굵어 정리해 두었기 때문에
한눈에 팍!!
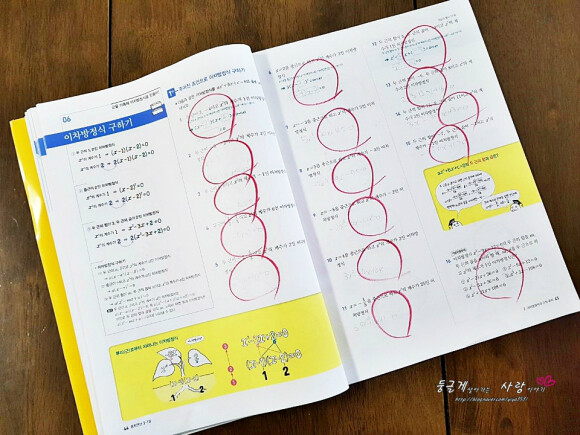
6. 이차방정식 구하기
< 근을 이용해 이차방정식을 만들어! >
이제껏 이차방정식의 근을 구하는 연습을 했습니다.
그럼 이제 반대로 근의 계수의 값이 주어졌을 때
주어진 조건을 만족하는 이차방정식도 구할 수 있어야겠죠?
두 근이 주어지고 x²의 계수만 알면 이차방정식을 구할 수 있답니다.
그리고 두 근의 합과 곱을 알고 x²의 계수를 알 때에도 이차방정식을 구할 수 있지요.

이차방정식 구하는 세 가지 조건을 이용해서
그에 맞는 공식을 잘 적용해서 한문제 한문제 열심히 잘 풀어주었습니다.
지금 이렇게 아이 학습 내용을 적고 있는데요~
참 우리 아이들이 외워할 할 것도 너무 많구나~
새삼 참 힘들겠다 ㅎㅎㅎ 그런 생각이 드네요.ㅠ

07. 계수가 유리수인 이차방정식의 해(근)
< 한 근이 주어질 때 다른 한 근 찾기! >
계수가 유리수인 이차방정식의 근은
유리수 부분은 같고 무리수 부분은 부호만 반대!
따라서 계수가 유리수인 이차방정식의 한 근을 알면
자연히 다른 한 근도 구할 수 있다는 말씀!!
이 또한 개념이 쉽게 정리가 되었기에
문제 푸는데 전혀 어려움이 없답니다^^

개념을 확인하는 " TEST "
2단원 이차방정식의 근의 공식 마지막 TEST를 해보는 시간이었습니다.
한 단원을 학습한 후 개념을 연결하는 통합 문제를
짧고 굵게 단 6문제로 평가해보았습니다.
개념이 정확하게 정리가 되었다면 당연히 오답이 나와서는
안되겠지요??ㅎㅎㅎ
네~~ 이 엄마의 걱정과 우려와는 달리
2단원에선 단 한문제의 오답이 나오지 않았더라고요.
생각보다 훨씬 잘 풀어주어서 안심이 되는 시간이었습니다.
이렇게 해서 디딤돌 중학연산 3-1B
2단원을 아이와 함께 풀어보면서 찬찬히 살펴보았는데 어떠셨나요?
중학교 수학은 초등학교 때와는 달리
개념적이고 추상적이므로 개념에 대한
정확한 이해가 무엇보다 중요한 시기라고하는데요
디딤돌 중학연산은 기초 개념에 대한 정확한 이해를 돕기 위해
최적의 방법을 제공하고 단계별로 충분한 문항을 통해
그 개념들이 익숙해지도록 구성하고 있답니다.
현재 한창 봄방학 기간이라 하루에 한장도 좋고 두세장까지
아침공부는 항상 디딤돌 중학연산 3-1B로 시작하고 있는데요
봄방학이 끝나기 전엔 충분히 끝낼 수 있을 듯 하네요^^
이번 겨울방학을 시작으로 봄방학까지
디딤돌 중학연산이 함께해줘서 얼마나 든든한지 모르겠어요^^
3학년 1학기 수학!!
디딤돌 중학연산으로 개념부터 탄탄히 구멍없이 확실히 잡을 생각입니다