-

-
이산수학 - 불연속적인 데이터를 다루는 기술 ㅣ 선생님도 놀란 초등수학 뒤집기 34
설한국 지음, 이원희 그림, 이광연 감수 / 성우주니어(동아사이언스) / 2011년 8월
평점 :

절판


바람이 넘 차졌죠?
어떻게든 늦가을을 버텨보려 했지만...
아그들을 감기에 보호하고자 하는 맘으로 보일러를 돌립니다. ^^
오늘은 이산수학에 대해 알아보도록 하겠습니다.
사실 저도 요부분은 쫌 어렵거든요.
그래도 초등수학뒤집기로 아이와 함께 열공했답니다.
일단 책을 2~3번 정도 읽으라 했습니다.
어찌나 책만 보면 인상을 구기는지...

여기선 먼저 개념에 대해서 집고 넘어가야 할것 같네요.
연속~은 끊임없이 모두 표시할수 있다!
이산~은 자료를 제한되게 표시한다는 뜻!
예를 들어서 이해를 해보죠.
운동경기중 애~매한 경기가 있을때 비디오 판독을 합니다.
움직임이 있는 연속된 장면을 끊어서 보여주기 때문에 요것은 이산!!
만화영화를 제작할때 한장면 한장면 정지된 것을 연속으로 이어서
마치 움직이는 것처럼 보이죠 요것을 연속!!
이해가 되셨나요??
아날로그와 디지털을 이해하고자 연속과 이산을 설명했습니다.
그럼 아날로그란 어떠한 수치를 연속된 양으로 나타내고,
디지털은 어떠한 수치를 끊어서 숫자로 나타내는 것을 말합니다.
고로 아날로그는 연속이라 부르고,
디지털은 이산이라 한다고 합니다.
그래서 집에 있는 물건들로 울 아들에게 아날로그와 디지털을 구분해 보았습니다.
아날로그는 손목바늘시계, 수은체온계
디지털은 핸드폰, mp3, 전자체온계

저는 이 책에 나오는 요 만화들 넘 잼난답니다.
볼때마다 표정이나 멘트들이 재미있어요. ^^

다음은 경우의 수 구하기입니다.
이부분은 우리아이 작년 1학년 학기말 수학책에 문제푸는 방법에서 나왔답니다.
남자아이라 그런지 요런거 넘 재미있어 합니다.
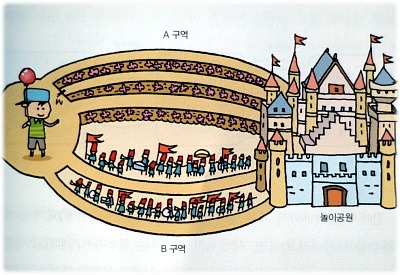
위의 그림처럼 A구역과 B구역이 있습니다.
꼬마가 서있는 곳에서 놀이공원까지 갈수있는 경우의 수를 구할때....
두사건이 일어나는 가짓수를 서로 더하는 것을 합의 법칙이라 합니다.
A구역(3가지) + B구역(2가지) = 5가지의 경우

집에있는 수학 도구를 이용해 보았습니다.
빨간색 못에서 갈수 있는 경우의 수를 아이에게 고무줄로 연결해 보라고 했지요.
초록색못(2가지) + 노란색못(2가지) = 4가지 경우의 수가 나오지요.
이렇게 합의 법칙을 알아보았습니다.
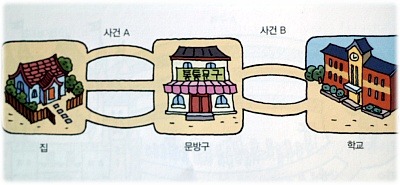
집에서 학교까지 갈수 있는 경우의 수를 알아보도록 하겠습니다.
우선 두사건이 일어나는 가짓수를 서고 곱하는 것을 곱의 법칙이라 합니다.
곱의 법칙에서는 사건A과 사건B가 서로 관련을 가지고 일어나야 합니다.
사건A(3가지) * 사건B(2가지) = 6가지 경우

빨간색에서 초록색과 노란색을 경유해서 초록색까지 가려합니다.
초록,노랑(4가지) * 파랑(2가지) = 8가지 경우의 수
다음으로 순열입니다. 우리아이가 위에 경우의 수를 이해하고 나서
순열에 대해서 더 빠른 이해를 보여주었어요.
순열이란 주어진 물건 가운데서 몇 개를 선택해서 어떤 순서로 나열하는 일입니다.
알파벳 a,b,c를 가지고 세칸에 채워보았습니다.

잘 하지요? ^^
아래의 그림 트리구조를 보면 경우의 수로 나타낼수도 있답니다.

각각의 알파벳에 2가지씩 나올수 있으므로
3 * 2 = 6가지
이산수학에서는 몇개의 점과 그 점들을 연결하는 선들을 모아 놓은것을 그래프라고 합니다.
그래프를 이루는 점을 꼭지점, 꼭짓점과 꼭짓점을 연결한 선을 변이라 합니다.
이산수학에서 말하는 그래프는 일반적으로 말하는 함수그래프와는 다르다고 합니다.
그래프의 변은 서로 다른 꼭지점을 적어도 2개의 꼭짓점이 있어야 합니다.
이 꼭짓점에서 나온 변의 개수를 차수라고 합니다.
아래의 그림이 이산수학에서의 그래프입니다.
a의 꼭짓점의 변 즉 차수를 2개
b의 꼭짓점의 차수는 4개
이해가 되셨지요? ^^

그럼 이 그래프로 한붓그리기를 해보겠습니다.
한붓그리기란 그래프에서 연필을 떼지 않고 모든 변을 오직 한 번씩만 지나는 것입니다.
저희도 어렸을때 이거 많이 했습니다. ^^

요기에도 비밀이 숨겨져 있네요.
차수가 홀수인 꼭짓점이 없거나 차수가 홀수인 꼭짓점이 2개일때만 가능하답니다.
그럼 그래프(A)의 한붓그리기만 가능하다는 말이죠.
차수가 홀수인 꼭짓점이 2개인곳....
그곳이 포인트였군요. ^^

로또란 글자를 보고 어찌나 나도 모르게 집중이 되던지...
요거 잘 연구해서 저도 한번 도전~~~~
이산수학에 이렇게 많은 원리가 들어 있었네요.
이런 많은 경우의 수로 가장 짧고 효율적인 경로를 찾는 알고리즘을 이용하는
이산수학... 참 매력있네요.
넘 어렵게만 생각했었는데 덕분에 아이와 재미있게 경험할수 있었습니다.