(체험) 바로 이것!! ˝중학수학 도형 - 한권으로 끝내기˝

중학수학 도형 한 권으로 끝내기 - 2015 개정교육과정 반영 / 중학교 1, 2, 3학년의 수학도형 '한권으로 완전정복'
고희권.장순자 지음 / 쏠티북스 / 2020년 5월

#중학수학도형

#중학수학도형한권으로끝내기

#쏠티북스

#중학교수학

#중학교도형

#중학도형

#수학도형

#중학교필수도형문제집

#반드시해야할도형문제집

#한권으로도형끝내기

#한권으로끝내기

#도형완전정복

“

중학수학 도형

한권으로 끝내기

”

쏠티북스에서 나온 "중학수학 도형 - 한권으로 끝내기"

{2015 개정교육과정 반영} 중학교 1·2·3학년의 수학도형 '한권으로 완전정복'

겉표지에 나와있는 문구 그대로

딱~ 그대로

엄마가 찾던.. 아이가 찾던.. 도형문제집이다.

① 중학교 1·2·3학년 모든 교과서를 완벽하게 분석하여 정리한 중학도형 총정리

② 어렵게 느껴지는 중학도형의 기본적인 개념을 완벽하게 정리할 수 있는 교재

③ 난이도가 점점 높아지는 단계별 반복학습을 통한 중학도형의 완벽한 이해

④ [1단계] 개념이해하기 → [2단계] 문제수준높이기 → [3단계] 응용문제도전하기

Never give up!

한권으로 중학과정의 모든 도형을 다루었다는 점이 가장 눈길을 끌었다.

올해 중1이 되는 첫째가 꼭 풀어봐야 할.. 문제집인 것이다.

초등학교 때부터 봐온 결과.. 수학을 좋아하지만 도형파트에서는 약한 모습을 보였던..아이

그래서 5학년 2학기 때에는 4권짜리 도형문제집(5학년수준)만 따로 풀린 적도 있었다.

대체적으로 여아들이 도형에 약하다고는 하지만,

이과를 생각하고 있는 첫째에게

도형은.. 필수적으로 정리하고 넘어가야만 했던 과제였다.

문제집이 도착하고 그날 바로 풀기를 시작하였다.

근데..아이가 문제집을 들고오며 "엄마, 요거 쉬운게 아닌데??" 라며 짜증을 부린다.

그래서 문제집의 차례를 다시 보았다.

테마별로 나와있어서.. 굳이 차례대로 풀지 않아도 되었던..

아이에게 다음~ 테마부터 풀라고 일러두었다.

결과적으로 아이가 조금은 편하게 생각했던 테마부터

02 -> 03 을 풀고 다시 01테마로 넘어와서 풀었다.

02, 03테마를 풀 때.. 어렵지 않다며

풀어보겠다고 자기방으로 들어가는 모습이 왠지 대견하면서도

언제 이렇게 컸는지.. 입가에 미소가 번졌다.

차례에서 나와있듯이 학년별 테마순서와 중요도 표시가 되어 있어

한눈에 쏙~ 들어왔다.

- 중학교 1학년 도형 총정리 -

이전에 배웠어요.

이번에 배워요.

이후에 배울 거예요.

그리고 수학 기호가 왼쪽에 그려져 있었다.

이젠 정말 중학생이 되는지라.. 한글보다 기호에 익숙해~ 져야 한다.

∴ 결론을 제시할 때, 사용하는 수학 기호

∵ 이유나 원인, 근거를 제시할 때, 사용하는 수학 기호

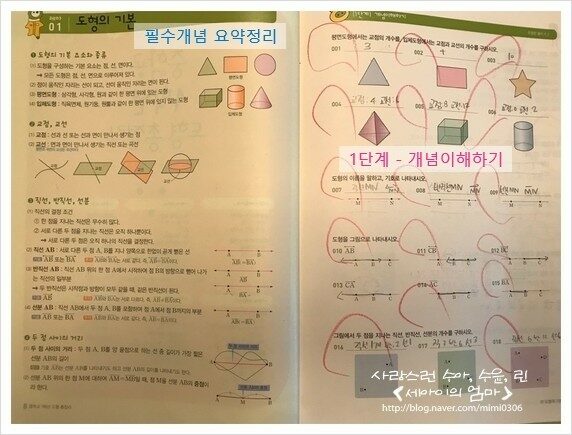
01. 도형의 기본

이 책의 구성과 활용을 어떻게 할 것인지가 파악된다.

[0단계] 필수개념 요약하기

도형도 마찬가지로 개념이 가장 중요하다고 생각한다.

그런점에서 도형의 개념설명과 예시, 주의, 참고 는 개인적으로 무척이나 마음에 들었다.

[1단계] 개념이해하기

필수개념을 정확하게 이해하고 첫번째로 푸는 단계이다.

개념이해하기 문제는 교과서에 실려 있는 문제 유형 을 그대로 가져와

교과서에서 제시된 접근 방식으로 기본 개념을 정확히 이해하도록 하였다.

비교적 무난하게 문제를 풀었던..

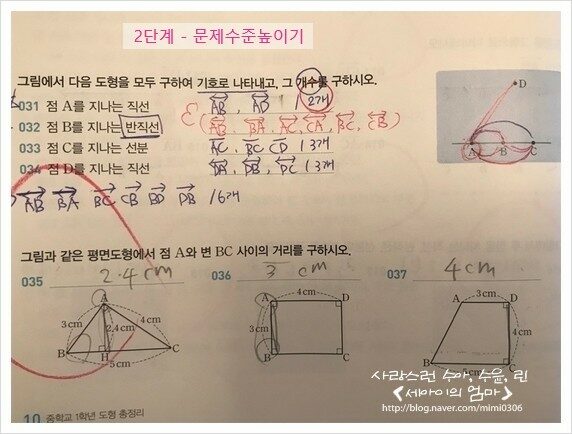
[2단계] 문제수준높이기

다양한 유형이 어느 것 하나 빠지지 않고 골고루 제시되어 반드시 풀어보아야 하는 단계 이다.

조금 어렵게 느껴졌다면 다시 개념을 익혀보자.

우리아이(중1)도 이부분에서 머리가 아팠는지..

조금 어렵네.. 라고 느꼈다고 한다. ^^;;

그러나 엄마의 도움없이.. 너무나도 잘 설명된 정답 및 해설 의 도움으로

다시 풀어나갔다.

초등학교 때 배웠던 직선, 반직선, 선분을 기호로 나타내며

도형을 찾는 문제이다.

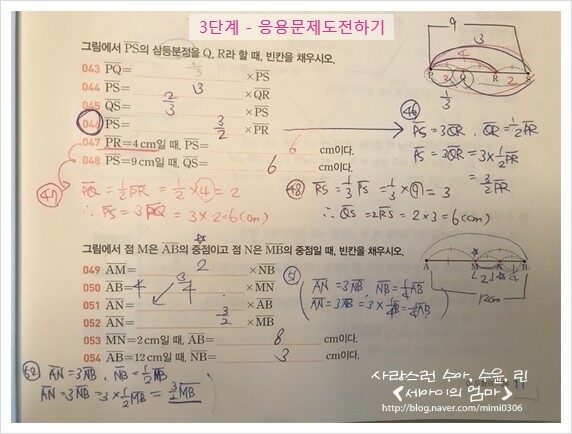
[3단계] 응용문제도전하기

1, 2단계가 개념을 이해했는지 확인하는 단계라면

3단계 응용문제도전하기 문제는 학교시험에 반드시 출제될 만큼 중요한 유형이거나

기본 개념을 응용 출제하여 사고력을 확장할 수 있는 유형을 엄선하였다.

역시 이부분에서 어려움을 많이 느낀..

선분의 중점을 이해하고 여러 유형의 문제를 풀어야 겠다.

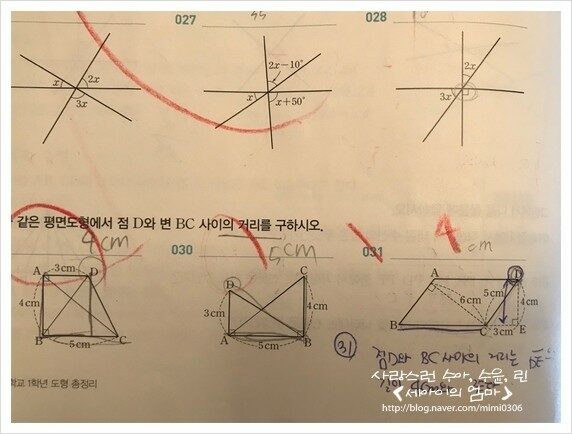
길이(cm)를 구하는 문제는 쉽게 푸는 반면

어느 선분의 1/2, 2/3.. 이런식의  문제는..

여러번 반복해서  풀어봐야 할 것 같다.

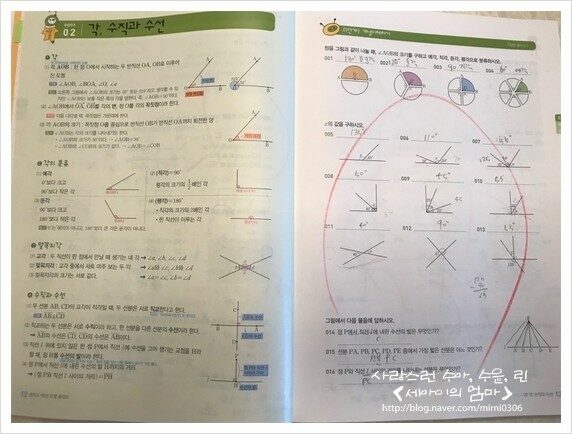
02. 각, 수직과 수선

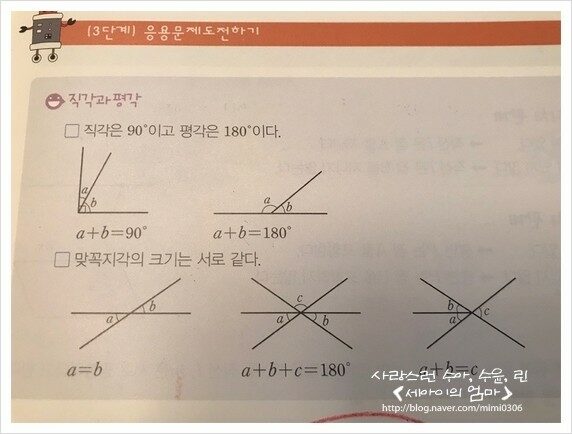
37번 문제 - 직각과 평각의 개념이해 문제이다.

『 직각은 90° 이고 평각은 180°

맞꼭지각의 크기는 서로 같다. 』

​를 이해하며 풀어야 한다.

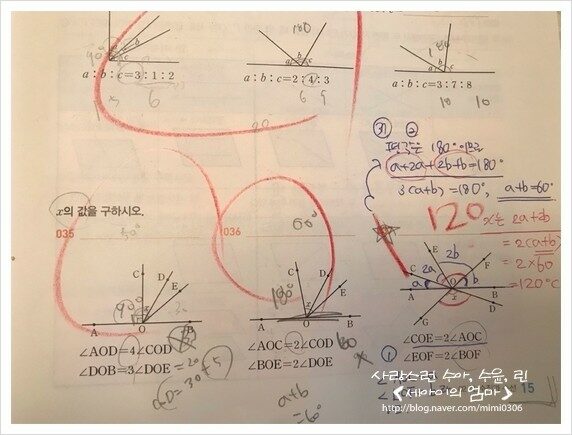
∠AOC = a , ∠BOF = b 라 하면

a + 2a+ 2b + b = 180° 이므로

3(a+b) = 180°​ , a+b = 60° 이다.

x는 2a + 2b 이므로

x = 2(a+b)

x = 2 × 60°

∴ x = 120°

03. 위치 관계

의외로 아이가 재미있어 했던 부분이다.

평면에서 두 직선의 위치 관계

공간에서 두 직선의 위치 관계

공간에서 직선과 평면의 위치 관계

공간에서 두 평면의 위치 관계

이렇게 3번째 테마까지 풀리고 보니..

중학도형은 초등도형과 달리 용어와 공식이 등장하고, 증명해야 한다는 점에서

갑자기 난이도가 올라간 느낌이 들었다.

지금도 단순 연산은 매일.. 하루에 10분정도 하고 있지만

도형은 정말.. 한달에 몇 번이라 아이들에게 익숙하지도 않은 것 같다.

그러나 중학도형을 제대로 이해하지 못하면 고등수학에서는 더 큰 어려움을 겪게 되고

도형으로 인하여 수포자가 생길 것이다.

이번 기회에 중학교 1·2·3학년 수학도형의 기본 개념을 한 권으로 익히고

단계별로 훈련하며 도형에 익숙하도록 해보자.

다른 문제집에 비해 손이 덜 가는 느낌이 들지만..

반드시 끝내야 하는 도형파트!!

한 권으로 끝낼 수 있다니, 정말 좋지 않은가?? ^^

우리아이는 올해 중1이라 예습겸 초등도형 복습겸 풀어나가야 겠다.

그리고 중3, 예비 고1의 경우에도

단기간에 중학 도형의 개념을 익히기에 너무 좋다.

바로 이것!!

"중학수학 도형 - 한권으로 끝내기"

세아이맘~ 강력추천해요!!

지금 살고 있는 현재 이 순간에 충실하라는 뜻의 라틴어로

'현재를 잡아라'로 번역된다.

우리아이의 좌우명이 된 것 같다.