평점
3점 ★★★ B
단어가 세상에 처음 태어났을 때의 모습을 ‘말밑’이라고 한다. 말밑과 비슷한 뜻의 단어는 ‘어원(語原)’이다. ‘아름답다’의 말밑은 어떻게 생겼을까? 여러 가지 가설이 있다. 내가 개인적으로 마음에 드는 가설은 ‘아름’의 말밑이 ‘앎’이라는 가설이다. “당신은 아름다워”를 말밑으로 풀어 써보자. “당신을 알아”가 된다. 상대방을 잘 알면 그 사람의 매력이 아름다워 보인다.
어떤 수학자는 수학 공식이 아름답다고 표현한다. 그들의 눈에는 복잡한 계산을 하지 않아도 되는 수학 공식이 아름다워 보인다. 하지만 수학을 좋아하지 않는 사람들은 도무지 이해할 수 없는 말이다. 《세상에서 가장 아름다운 수학 공식》은 수학을 공부할 때 알아야 할 49개의 수학 공식을 소개한 책이다. 이 책을 펼친 독자가 알아야 할 것은 수학 공식의 기원이다. 그렇다고 해서 수학 공식이 탄생하는 과정까지 달달 외울 필요 없다. 수학 교과서에 갇힌 수학 공식은 딱딱하다. 전혀 아름답지 않다. 알고 싶은 마음이 생기지 않는다. 하지만 수학 교과서에 갇히지 않은 수학은 자유롭다. 그래서 교과서가 정해준 대로 수학을 공부하지 않아도 된다. 수학 공식이 어떻게 만들어졌는지 알고 나면 수학이 부드러워진다. 반면 수학 교과서는 학생을 가르치듯이 수학 지식을 알려준다. 일단 먼저 수학 공식을 처음 만든 수학자를 소개한다. 그리고 본론으로 들어간다. 수학 공식을 이용해 문제를 푸는 방식을 알려준 다음에, 이를 응용해서 문제를 풀어보라고 지시한다. 이러니 수학이 딱딱하고 재미없다.
《세상에서 가장 아름다운 수학 공식》은 콩트 형식으로 수학 공식을 소개한다. 수학 콩트의 주인공은 수학자가 아니다. 수학을 전문적으로 공부한 적이 없는 평범한 사람들이다. 호기심이 많은 소년은 빈센트 반 고흐(Vincent van Gogh)의 <해바라기>가 그려진 포스터에 접힌 자국을 우연히 발견하고, 이를 이용해 포스터의 면적을 구한다. 이 과정에서 소년은 피타고라스 정리(직각삼각형 정리)를 발견한다. 존 네이피어(John Napier)라는 수학자가 고용한 정원사는 정원의 넓이를 구하기 위해 계산하다가 훗날 ‘로그(log)’라고 불리게 될 수학 개념을 도출한다.
피타고라스 정리를 스스로 발견한 소년과 네이피어의 정원사는 허구 인물이다. 왜 이 책의 저자는 왜 수학 콩트의 주인공을 수학자가 아닌 사람으로 내세웠을까? 수학은 상아탑 안에서만 놀기 좋아하는 수학자들을 위한 학문이 아니다. 수학 공부를 좋아하지 않는 우리가 알게 모르게 수학은 실생활에 가까이 있다. 이 책은 수학 공식이 실생활에서 어떻게 활용될 수 있는지를 보여준다. 호기심과 인내력이 있으면 수학자가 아닌 사람들도 수학의 매력에 빠진다.
저자는 수학적 사실을 왜곡하는 문제를 피하면서 허구를 가미한 수학 콩트를 썼다. 책 끝부분에 저자는 수학 콩트를 쓰면서 자기가 지어낸 장면을 상세하게 설명했다. 그래도 책 속에 ‘사실과 다른 내용’이 있다. 저자는 화가들이 황금비가 적용된 ‘아름다운 사각형’을 알고 있다고 주장한다. 그러면서 레오나르도 다빈치(Leonardo da Vinci)의 그림 <수태고지> 속에 숨겨진 황금비를 보여준다(70~71쪽). 황금비의 아름다움을 옹호하는 사람들은 예술가들이 황금비에 맞춰 그림을 그렸거나 건축물을 세웠다고 믿는다. 하지만 근거가 없는 믿음이다. 예술 작품에서 황금비를 측정하는 방식은 오래전에 수학자들도 지적한 ‘수학적 왜곡’이다.
이 책에 수학자들의 일화가 나오는데, 대부분은 허구이며 후세에 지어진 것들이다. 러시아의 황제 예카테리나 2세(Ekaterina II)는 프랑스의 철학자 드니 디드로(Denis Diderot)에게 신이 존재하느냐고 물었다. 종교를 비판한 계몽주의자 디드로는 신이 존재하지 않는 이유를 설명했다. 그러나 황제에게 총애받아 러시아에 체류하게 된 스위스의 수학자 오일러(Leonhard Euler)는 아주 간단하게 수식을 제시하면서 신은 존재한다고 대답했다. 수학 공식을 알지 못하는 디드로는 오일러의 주장에 반박하지 못했다.

저자는 오일러, 디드로, 러시아 황제가 나눈 대화는 실제로 있었던 일이라고 주장한다(190쪽). ‘천재 수학자’로 평가받는 오일러의 영특함을 보여주는 이 일화는 수학사에 많이 언급될 정도로 유명하다. 그러나 실제로 있었던 일이 아니다. 일화의 원전에 오일러가 아닌 러시아 출신 철학자가 나온다. 일화가 변형된 채 와전된 것이다.[주]

뉴턴(Isaac Newton)이 땅에 떨어진 사과나무를 보는 순간, 만유인력의 법칙을 생각했다는 일화(192쪽) 역시 사실이 아니다.
이 책의 39장은 ‘쾨니히스베르크의 다리 건너기’ 문제에 관한 이야기다. 쾨니히스베르크는 과거에 독일의 영토였다. 쾨니히스베르크를 지나가는 강에 일곱 개의 다리가 있었다. 누군가가 이 일곱 개의 다리를 한 번씩만 건너서 출발 지점으로 돌아올 수 있는지 궁금했다. 이러한 방식을 ‘한붓그리기’라고 한다. 오일러는 한 번에 모든 다리를 건너가는 일은 ‘불가능’하다고 증명했다.
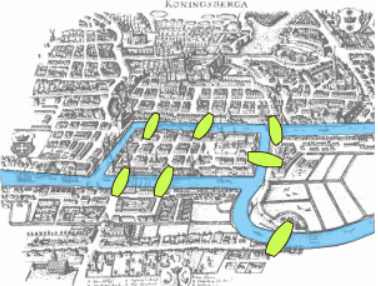
쾨니히스베르크의 다리.
원래는 일곱 개의 다리가 있었다.
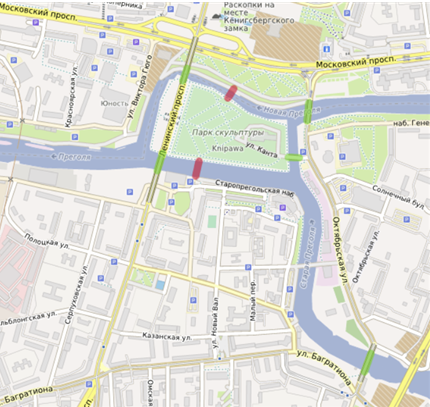
칼리닌그라드의 다리가 있는 현재 지도.
녹색으로 표시된 다섯 개의 다리는 현재 남아 있는 다리다.
빨간색으로 표시된 두 개의 다리는 전쟁 중에 파괴되어 사라졌다.
(사진 출처: 위키피디아)

제2차 세계대전 이후에 쾨니히스베르크는 러시아(당시 국명은 소련)의 영토가 되었다. 현재 지명은 칼리닌그라드다. 저자는 ‘여덟 번째 다리가 새로 건설되어서’ 이제는 한 번에 건너는 일이 가능하다고 말한다(150쪽). 하지만 현재 남아 있는 다리의 개수는 총 다섯 개다. 두 개의 다리는 제2차 세계대전 중에 폭파되어 소실되었다. 현재 다섯 개의 다리로 한붓그리기가 가능하지만, 무조건 출발점으로 돌아올 수 없다.
[주] 참고문헌: 박부성 《천재들의 수학 노트》 (향연, 2003년)