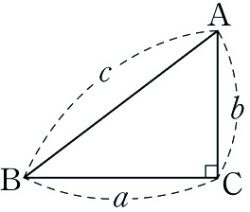
피타고라스의 정리 :
-직각삼각형에서 직각을 낀 두 변의 길이를 각각 a, b라 하고, 빗변의 길이를 c라 하면 a+b=c이 성립한다.
간단하면서도 완벽하고 아름다운 방식으로 진리를 서술하는 정리인 피타고라스의 정리는 모르는 사람이 없을 정도로 유명하다. 피타고라스의 정리는 현대 인류 문명의 지식을 지탱하는 근간 중 하나로, 초기 인류사의 한 획을 그은 위대한 발견 중 하나로 꼽힌다.
찬란했던 피타고라스 시대 이후로 16세기에 이르기까지 수학의 발전은 정체되어 있었다. 17세기에조차 사람들은 옛날 피타고라스나 유클리드, 디오판토스 등 고대 그리스 수학자들의 책을 겨우겨우 읽을 뿐이었는데, 이때 페르마라는 괴상한 천재가 나타난다.

17세기의 수학자 피에르 드 페르마
혼자 이러저러 계산하길 좋아했던 페르마는 피타고라스의 정리 a+b=c를 살짝 꼬아 다음과 같은 새로운 식을 만들어 봤다.
a+b=c
a+b=c
a+b=c
지수가 2제곱인 피타고라스의 정리에서는 식을 만족하는 해가 끝없이 많았지만 이상하게도 지수를 3제곱이나 그 이상의 숫자로 바꿨을 때는 아무리 계산을 해봐도 해가 단 하나도 나오질 않는 것이었다. 이 이상한 현상에 매료된 페르마는 상당한 시간을 계산에 쏟아붓고는 다음과 같은 결론을 내린다.
"n이 3 이상의 정수일 때, x^n+y^n=z^n을 만족하는 양의 정수 x, y, z는 존재하지 않는다. "
이것이 바로 페르마의 마지막 정리이다. 이후 페르마는 자신이 읽던 수학 책 귀퉁이에 향후 350년간 수많은 수학자들을 파멸의 구렁텅이에 밀어 넣을 악명 높은 메모를 휘갈겨 놓았다.
"나는 이 정리를 경이로운 방법으로 증명에 성공했지만, 책 여백이 너무 좁아서 여기엔 쓰지 않겠다."
페르마가 남겨놓은 다른 정리와 증명들은 후세대 수학자들에 의해 모두 오류가 없는 것으로 판명되었지만 이 페르마의 마지막 정리는 끝까지 증명되지 않아 '마지막'정리라는 이름이 붙게 되었다.
당시 페르마가 진짜로 증명에 성공했는지는 영원히 알 수 없다. 다만, 페르마의 성품과 그의 다른 증명들이 오류가 없었다는 것 등을 근거로 아마 페르마라면 진짜 증명했을 거라는 설이 우세하다. 특히 페르마가 a+b=c의 경우나 a+b=c의 경우에는 신뢰할 만한 방법으로 힌트를 남겨놓았기 때문에(이것들을 적을 여백은 있었던 모양이다.) 후세대 수학자들은 페르마의 힌트를 통해 n이 3인 경우와 4인 경우 등 단편적인 증명에 성공하기는 했다. 다만 페르마의 마지막 정리의 n값은 무한했기 때문에 이렇게 하나씩 증명해서는 페르마의 마지막 정리를 영원히 증명해내지 못할 것이었다.
페르마가 17세기에 증명해냈다고 주장한 문제를 상당한 수학적 기교들이 개발된 이후 세대 수학자들도 증명하지 못한다는 점에서 수학계는 자존심에 상당한 타격이 있었고, 페르마의 마지막 정리가 외견상으로는 상당히 간단해 보이기 때문에 페르마의 마지막 정리를 증명하겠다고 도전한 수학자들이 많았다. 하지만 이들 모두는 인생의 상당한 시간을 허비하고도 증명에 실패했고, 수많은 천재들이 자살과 정신병 등으로 비극적인 말로를 맞게 된다.

향후 페르마의 마지막 정리를 증명하는데 결정적인 기여를 한 '모듈러성 정리(다니야마-시무라의 추측)'를 발견한 다니야마의 유서. 몇 주 후 결혼할 약혼녀를 남겨두고 돌연 자살했다.
간단한 피타고라스의 방정식을 살짝 꼬았을 뿐인 간단한 방정식의 증명이 최악의 난제로 변해버린다는 점이 참으로 신기할 따름이다. 책은 이 악명 높은 페르마의 정리를 주제로, 수학사 전반을 걸치는 이야기를 재미있게 풀어나가며, 페르마의 마지막 정리에 대해 설명한다. 저자의 스토리텔링 실력이 상당해서 글에 군더더기가 없으며 정말 재미있게 술술 잘 읽혀 청소년 독자들에게도 무리가 없을 정도이다. 이 책 스토리 그대로 영화로 만들어도 대박칠 수 있을 것 같다.
페르마의 마지막 정리는 94년에 앤드루 와일즈라는 천재 수학자가 외부와 고립된 채 8년이라는 시간을 쏟아 부운 끝에 결국 증명되고 만다. 이는 수학 사상 최고의 대사건으로 책은 당시 수학계의 흥분을 실감나게 묘사하고 있다. 94년 당시에 나는 유치원생이었기에 이런 대사건의 전 지구적 흥분을 체감하지 못한 채 보내버린 것이 아쉬울 따름이다.
수학이란 분야가 얼마나 재미있고 대단한 것인지, 왜들 그렇게 미친 듯이 파고드는 것인지, 이 책을 보면 이해가 된다. 수학이란 자연을 기술하는 도구로써, 수학적 증명의 탐구는 결국 만고불변의 진리를 탐구하는 것이다. 수학자와 과학자는 진리의 탐구라는 같은 길을 걷되 다른 도구를 사용하는 것일 뿐이다. 과학자는 현장에서 관찰을 통해, 수많은 실험과 이론의 수정을 통해 진리를 파헤치지만 수학자는 그저 책상 앞에 앉아서, 수학과 논리만을 무기로 온 우주에 공통적으로 적용되는 절대진리를 찾아낸다.
나는 학창시절 수학에 관심을 갖지 못했다. 고리타분한 방정식들을 도대체 "왜" 배워야 하는지, 배워서 어디다 써먹는 것인지, 이게 도대체 어디가 재미있다는 것인지 전혀 알지 못한 채 그저 수학 책의 내용을 주입받았을 뿐이었고, 이에 거부감을 느꼈기 때문이었다. 결국 나는 흔히 말하는 '수포자'로 인문계열로 진학했다. 이 때의 진로선택으로 나는 오늘날에 이르기까지 상당한 시간을 낭비해야만 했다.
요즘 학교는 어떤지 모르겠지만 학교에서는 주입식 교육 이전에 이런 책을 읽혀야만 한다. 학생들이 고리타분해 보이는 수학을 왜 배워야 하는지 이해하고, 수학에 흥미도 느끼게 해 주는 최고의 방법일 거라고 생각한다. 당시에 내가 이 책을 읽었다면 내 인생이 바뀌었을 거다. 수학을 어려워하는 자녀가 있다면 반드시 이 책을 권하길 추천한다. 그 아이가 나처럼 학창시절을 후회하는 어른이 되지 않도록.