‘세상에 바뀌지 않는 사실은 ˝세상 모든 것은 바뀐다˝는 사실이다.‘

튜링 & 괴델 : 추상적 사유의 위대한 힘 ㅣ 지식인마을 36
박정일 지음 / 김영사 / 2010년 11월

<튜링 & 괴델>은 튜링의 '보편 튜링 기계'와 괴델의 '불완전성 정리'의 개념을 중심으로 현대 수학의 집합론과 컴퓨터에 대해 설명한 수리논리학 입문서다. 

<튜링 & 괴델>에서는 두 수학자의 이론이 다루어진다.

영화 <이미테이션 게임 Imitation game>으로 유명한 튜링(Alan Mathison Turing, 1912 ~ 1954)의 '보편 튜링 기계'를 설명하기 위해 <튜링 & 괴델>에서는  프레게(Friedrich Ludwig Gottlob Frege, 1848 ~ 1925)의 <개념 표기법 Begriffsschrift>(1879)상의 '문장 논리'와 '술어 논리', 칸토어(Georg Ferdinand Ludwig Philipp Cantor, 1845 ~ 1918)의 '집합론'의 개념을 연관설명하고 있다. 또한, 괴델(Kurt Godel, 1906 ~ 1978)의 '불완정성 정리'를 설명하기 위해 힐베르트(David Hilbert, 1862 ~ 1943)의 '힐베르트 프로그램'의 개념을 소개한다. 

프레게는 기존 아리스토텔레스(Aristoteles, BC 384 ~ 322)의 삼단논법으로 대표되는 기존 논리학 대신 문장연결사를 활용한 '현대 논리학'을 창시했으며, 현대 논리학과 무한(infinty)의 개념을 잠재무한(potential infinity)과 실제무한(actual infinity)으로 구분한 칸토어의 '무한론'은 튜링기계(Turing machine)의 이론적 토대가 된다. 책에서는 튜링 기계의 작동원리가 후대 컴퓨터 특히 인공지능(AI)과 어떤 방식으로 연결될 수 있는지가 '보편 튜링 기계(universal Turing Machine)'를 통해 설명된다.

'간단히 말하면 보편 튜링 기계란 다른 튜링 기계가 할 수 있는 모든 일을 흉내낼 수 있는 기계를 말한다(p108)... 그렇다면 보편 튜링 기계가 의미하는 바는 무엇인가? 보편 튜링 기계에서는 다른 튜링 기계의 프로그램이 하나의 수치로, 다시 말해 하나의 데이터로 입력되고 처리된다'(p123)

[그림] 알파고 서버(출처 : http://www.insight.co.kr/newsRead.php?ArtNo=54225)

괴델의 불완전성 정리는 '제1불완전성 정리'와 '제2불완전성 정리'로 나눌 수 있다.

'수학의 체계가 무모순이라면, 수학의 체계에서는 참이지만 증명할 수 없는 명제가 존재한다는 것이다(제1불완전성 정리). 나아가 수학의 체계가 무모순이라면, 수학의 체계에서 모순이 도출되지 않는다는 것을 그 체계에서는 증명할 수 없다는 것이다.(제2불완전성 정리)' (p161)

'한 문장에 대해서 그 자신과 그것의 부정이 동시에 증명 불가능한 경우, 그 문장을 결정 불가능한 문장이라고 부르며, 이를 "괴델의 제1불완전성 정리"이다.'(p167).. 괴델은 산수 체계의 무모순성이 그 체계 내부에서 증명될 수 없다는 것을 증명했다.'(p180)

<튜링 & 괴델>에서는 각각의 명령어가 어떤 방식으로 개별 숫자에 대응할 수 있는지를 보여주고, 이러한 수대응(數對應)이 무한히 계속될 수 있음을 통해, 보편 튜링 기계의 작동이 '멈추지 않는다'는 것을 보여주고 있다. 그리고, 이러한 개념은 '기계는 생각할 수 있는가?'의 문제제기로 이어진다. 책에서 제기한 이러한 질문에 대해 2015년 알파고와 이세돌의 바둑 게임 결과로 답을 할 수 있다고 생각된다. '기계학습'을 통해 발전하는 인공지능(AI)의 시대를 살아가는 우리에게 <튜링 & 괴델>은 컴퓨터의 기본개념에 대해 잘 설명해주는 좋은 입문서라 생각된다.

[그림] 바둑의 경우의 수( 출처 : http://www.bloter.net/archives/249668)

이러한 입문서로서의 역할 이외에도 <튜링 & 괴델>은 수리논리학이 결코 <수학 정석>의 집합, 명제 수준이 아님과 수학의 여러 정리를 추가적으로 제시하여 독자의 흥미를 더한다. 그 중 두 가지를  소개해본다.

1. 부랄리-포르티 역설과 안셀무스의 신 존재 증명

<튜링 & 괴델>에서는 칸토어의 역설을 설명하면서 '부랄리-포르티 역설'을 설명하고 있는데, 이는 중세 안셀무스의 신 존재 증명을 연상시킨다. 서양에서 무한(infinity)라는 개념은 신(God)의 존재와 뗄 수 없는 관계라는 생각이 든다.

[부랄리-포르티 역설]

모든 서수들의 집합은 존재하는가? 다시 말해 가장 큰 서수는 존재하는가? 이를 증명하기 위해 가상의 집합 Ω를 가정하자. 이 집합에는 0, 1, 2, 3, ... ω(초한 서수)가 포함될 것이다. 모든 서수들의 집합 Ω의 서수는 Ω의 원소인 어떤 서수보다 크며, 가장 큰 서수가 될 것이다. 그런데 Ω로부터 Ω+1을 구성할 수 있다. 또한 Ω+1은 Ω보다 더 크다. 그러나 이는 가 가장 큰 서수라는 사실과 모순된다.(p142)

[안셀무스의 신 존재 증명] 

1. 신은 그보다 더 큰 것이 상상될 수 없는 존재다.(가장 큰 존재다.)

2. 이런 신의 개념은 인간의 지성 속에 존재한다. (즉, 그런 개념을 인간이 이해할 수 있다.)

3. 신이 실재가 아닌 마음 속에만 존재한다고 가정하자.

4. 그것은 마음 속에 한정된 신보다 더 큰 개념이므로, 그보다 더 큰 것이 상상될 수 없는 존재라는 신의 정의에 모순된다.

5. 따라서 신은 실제로 존재한다. (출처 : 위키피디아)

2. 러셀의 역설(Russell's paradox)

책에서는 자기 지시의 모순의 대표적 예로 러셀의 역설을 소개한다.

[그림] 러셀의 역설( 출처 : 네이버)

S라는 집합을 "자신을 원소로 포함하지 않는 모든 집합들의 집합"으로 정의하자. 다시 말해, A가 S의 원소가 되기 위한 필요충분조건은 A가 A의 원소가 아닌 것으로 한다. 이 경우 "S는 S의 원소이다"라는 명제와 "S는 S의 원소가 아니다"라는 명제는 둘 다 모순을 도출하여 맞다 혹은 그르다 중에 어떤 답으로 답할 수 없다. (출처 : 위키피디아)

러셀의 역설을 이용해서 한 가지 명제를 만들어 보면서 리뷰를 마치고자 한다.

'세상에 바뀌지 않는 사실은 "세상 모든 것은 바뀐다"는 사실이다.'

PS. '분명하게 말할 수 있는 것은 "모든 것을 분명하게 말할 수는 없다."라는 사실이다' 라는 명제 때문에 비트겐슈타인(Ludwig Josef Johann Wittgenstein, 1889 ~ 1951)것이 '말할 수 없는 것에 대해 침묵해야한다'고 한 것은 아닐테지... 

<신의 베틀> : 수학(數學)과 종교(宗敎)

신의 베틀 ㅣ 경문수학산책 18
클리퍼드 픽오버 지음, 이상원 옮김 / 경문사(경문북스) / 2002년 1월

<신의 베틀>은  '수(數)'와 '신(神)'과의 관계를 과학소설의 형식을 빌려 표현한 과학 소설(SF)이다. 작품의 큰 틀은 서기 2080년을 살고 있는 주인공이 기원전 450년으로 돌아가 '피타고라스'를 만나고, 그의 애인인 '테아노'와 사랑에 빠져 함께 시간 여행을 한다는 내용의 소설이다. 마치 어린이 '공룡 백과 사전'의 시간 여행을 연상시키는 <신의 베틀>의 구조는 단순하고, 어설픈 주인공과 피타고라스 애인과 사랑 이야기는 어설프지만, 책에서 다루는 과학사적 내용은 상당히 흥미롭게 빠져들게 만든다.

<신의 베틀>에서 다루는 주요 내용은 피타고라스의 수비학(數秘學), 성(聖) 아우구스티누스와 수, 프랙털(fractal), 카발라(Kabala), 괴델의 신의 존재에 대한 수학적 증명등으로 수학(數學)과 종교(宗敎)와의 관계가 흥미롭게 분석되어 있다. 특히, '신의 존재에 대한 괴델의 수학적 증명'은 평소 관심있던 내용이라 개인적으로 더 흥미로웠다. 다음에서 다루는 책의 주요 내용을 정리해 보면 다음과 같다.

1. 피타고라스의 수비학

우리에게는 '피타고라스 정리'로 유명한 수학자지만, 사실 그' 피타고라스 학파'라는 집단의 우두머리였다. 이 학파는 '수(數)'를 통해 우주적 질서를 파악한 일종의 종교집단으로 그들만의 금기사항으로도 유명하다. <신의 베틀>에서는 피타고라스 학파의 특징과 함께 삼각수, 오각수의 비밀등을 다루고 있다.

'수, 수적 비례, 그리고 조화에 대한 연구와 고민은 피타고라스 학파의 가장 큰 특징이었다. 수는 사물과 닮았고 많은 경우 사물 자체이기도 했다.... 피타고라스 학파에서 짝수는 여성이고, 홀수는 남성이다. 1이라는 숫자는 모든 수의 근원이고 2는 첫 번째 여성수다. 첫 번째 남성수는 3이고 이것을 첫 번째 여성수와 더하면2+3=5가 되어 결혼을 생각한다. 8은 결혼을 상징하는 5에 남성수인 3이 더해진 수로 사랑의 비밀을 간직한 것으로 여겨졌다.'(p38)

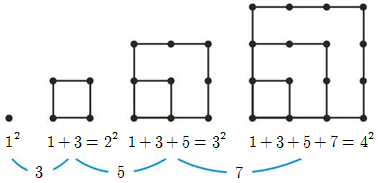
[그림] 피타고라스의 삼각수 (출처 : http://guestbook.blog.naver.com/PostView.nhn?blogId=alwaysneoi&logNo=220090463291&parentCategoryNo=21&categoryNo=&viewDate=&isShowPopularPosts=false&from=postView)

2. 성(聖) 아우구스티누스와 수

우리에게 <고백록>으로 유명한 아우구스티누스에게 수학은 성경 해석의 도구였다. 성경의 구절에 적힌 숫자들의 의미를 교리에 따라 해석한 내용이 <신의 베틀>에서 다루어진다.

'성 아우구스티누스는 153이 신비스러운 수이고 말세가 되면 성인 153명이 되살아난다고 믿었어... 성 아우구스티누스는 숫자를 사용해 성경을 해석했거든. 예를 들어 그는 사도들이 티베리아(Tiberia) 바다에서 물고기 153 마리를 잡았다는 신양성서(요한 21:11)에 주목했지. 인간이 10계명을 지킬 수 있도록 해주는 성령의 일곱 가지 선물에서 착안해 이 제자들이 성자임에 틀림없다고 생각한거야. 또한 10+17=17이고 1에서 17까지의 수를 모두 더하면 153이 나오지.'(p122)

3. 프랙털(fractal)

작은 크기의 모양이 끊임없이 반복되는 '자기닮음성'을 보여주는 프랙철이 컴퓨터에 의해서 만들어지는 인위적인 현상이 아니라, 양치류 등의 자연을 통해서도 나타남을 설명한다.

'프랙털이란 같은 모양이 크기를 달리해 반복되는 형태를 말해요. 나뭇가지 안에 다시 조그만 나뭇가지들이 들어 있는 모양이라고나 할까. 수학자들은 그런 구조를 자기 닮음(self-similar)라고도 불러.'(p242)

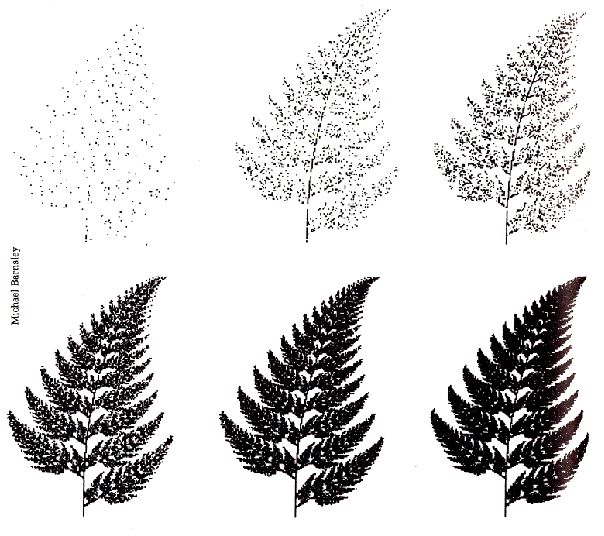
[그림] 프랙털(출처 : http://www.aistudy.com/physics/chaos/shape_gleick.htm)

4. 카발라(Kabala)

성서의 해설은 기독교만의 전유물은 아니었다. 유대교에서도 이러한 경향이 있음을 <신의 베틀>을 통해 확인할 수 있다.

'카발라란 12세기와 그 이후에 널리 퍼진 유대인들의 비밀스러운 신비주의야. 그들은 구약석서의 대부분이 암호라고 말하지.(p314)... 카발라에서는 또한 수를 통해 네 글자로 된 신의 이름을 이해하려고 했어. 그 신의 이름은 IHVH라고 씌여 있고 그 발음은 야훼 또는 여호와 정도가 되지만 너무도 신성한 것이었기 때문에 소리내어 읽으면 안 된다고 했지....카발라에 따르면 야훼라고 하는 간단한 이름은 본래 72음절 216글자로 이루어진 진짜 신의 이름을 짧게 부르는 것에 불과해. 이 신성한 이름은 셈 하-메포라시(shem ha-meforash)라고 불리지.' (p319)

5. 신의 존재에 대한 괴델의 수학적 증명

<신의 베틀>에서 불과 1페이지 정도에 이르는 증명을 소개하면서 약 20페이지에 걸쳐 이에 대한 현대 수학자 및 철학자들의 견해를 [부록]으로 설명한다. 내용이 어려워 다 이해하기는 어렵지만, 안셀무스와 토마스 아퀴나스의 신존재 증명(다섯 가지 길)과는 또 다른 관점을 알게 된다.

공리1. (이분법) 속성은 그 부정이 부정적일 경우에만 긍정이다.

공리2. (닫힘) 속성은 긍정적인 속성을 가진 경우에만 긍정이다.

정리1. 긍정적 속성은 논리적으로 일관된다. (다시 말해 실례를 가질 수도 있다.)

정의. 모든 긍정적인 속성을 가지는 것만이 신적이다.

공리3. 신적이라는 것은 긍정적인 속성이다.

공리4. 긍정적인 속성이 되는 것은 (논리적으로) 필요하다.

정의. x가 P를 최소한으로 가지고 있을 경우에만 속성P는 x의 핵심이 된다.

정리2. x가 P를 최소한으로 가지고 있을 경우에만 속성 P는 x의 핵심이 된다.

정의. NE(x) : 핵심 속성을 가지고 있다면 x는 반드시 존재해야 한다.

공리5. 반드시 존재한다는 것은 신적이다.

정리3. 신적인 x는 반드시 몇몇 개가 존재한다. (p382)

<신의 베틀>은 수학과 종교의 관계를 어떻게 보고 있을까?  저자는 서문에서 다음과 같이 말하고 있다.

'신은 정말로 수학자였을까?... 나는 신이 수학자였는지 아닌지 모른다. 하지만 신이 우주라는 천을 짜 내려갈 때 수학이 그 베틀 역할을 했음은 틀림없다고 믿는다.'(p3)

<신의 베틀>에서는 이처럼 우주의 근본질서가 되는 근본원리로서 '수학'을 조명한다. 그리고 피타고라스 이래 수학이 종교와 신의 섭리를 설명하기 위해 어떻게 사용되었는지를 알려준다. 약 400페이지가 넘는 분량이지만, 양(量)에 비해  쉽게 읽을 수 있는 편이다. 그 이유는 무엇 때문일까? 나는 <신의 베틀>이 재밌게 읽히는 것은  '문과'에 속하는 '종교학'과 '이과'에 속하는 '수학'이 결코 다르지 않다는 것을 보여주면서, '문과-이과'의 구분에 익숙한 우리의 편견을 깨기 때문이라고 생각한다. 그리고, 다음과 같은 생각을 해본다.

우리 나라 교육과정은 크게 문과(文科)와 이과(理科)로 나누고 있다. 그리고, 진학 기준을 수학을 잘하는가에 따라 큰 방향을 결정하고 있는 것이 현실이다. 그렇지만, 실제로 전공을 깊게 공부하다보면 모든 학문이 서로 연결되어 있음을 직접 체감하게 된다. 이른바 사회과학이라고 불리우는 분야에 있어서는 이공계만큼의 많은 수학공식이 필요하며, 공학분야에도 인간에 대한 고려 등 철학이 필요하다는 것은 공부를 깊이할수록 절감하게 된다. 이런 부분을 고려한다면, '문-이과' 체계가 합당한 학문 분류 체계인지 다시 고민하게 된다.

PS. '신의 존재에 대한 괴델의 수학적 증명'을 찬찬히 읽어보면 '스피노자(Spinoza)'적 관점이 눈에 띈다. '정의. 모든 긍정적인 속성을 가지는 것만이 신적이다.'에서 '부정은 단지 유한한 피조물에서만 발견되는 속성'이라고 말한 <Ethica>의 관점을 볼 수 있다.

｀자｀와 ｀컴파스｀로 그리는 이데아(Idea)의 세계

기하학원론 - 가 - 평면기하
유클리드 지음, 이무현 옮김 / 교우사(교재) / 1997년 1월

<기하학 원론-가>는 유클리드의 <원론Στοιχε?α, 스토이케이아, Elements of Geometry>중 1권부터 4권까지의 내용을 정리한 책이다. '가'에 해당하는 내용은 1권 직선/ 각/ 삼각형, 2권 도형의 넓이, 3권 원, 4권 정다각형의 원을 주제로 논의를 확장시켜 나간다.

<원론>은 앞 뒤의 내용이 체계적으로 연관되어 있는 구조를 가지고 있다. 

각권의 처음은 '뜻매김', '공리', '상식'을 통해 증명을 위한 기본사항을 약속한다. 각 권의 시작에 '뜻매김(정의)'를 통해 이름을 짓고, '공리'를 통해 사실로 받아들여야할 사항을 정리한다. 마지막으로 '상식'은 일반적으로 우리가 받아들일 수 있는 사항들이며, 이들은 증명을 위한 기본 사항이다.

이러한 기본 사항에 동의한 후 우리는 '도형의 작도'를 통해 본격적인 '법칙'을 증명하게 된다. 매 문제 단위로 법칙을 증명하면, 다음 법칙 증명 시 전에 입증한 법칙이 또다른 '상식'으로 다음 증명에 활용된다. 우리가 몰랐던 사실들이 '상식'으로 받아들여지면서, 직선에서 정다각형으로 우리의 '앎'이 나가는 과정이 책의 목차(Index)다. 그래서, <기하학 원론>의 유기적 구성 자체에서 '건축물' 같은 느낌을 받게 된다.

[그림1] 가우디 건축물 (사진출처 : http://blog.daum.net/whitebooks/6039889)

각 법칙을 증명할 때 사용하는 기본 패턴이 존재한다.

예를 들어서, 삼각형의 닮음을 증명할 때는 일단 임의의 점(點)선정, 평행한 선분, 선분의 연장, 내접 또는 외접하는 원을 그려서 증명하는 방식을 취한다. 대부분의 증명방식은 이러한 방식으로 활용하여 증명을 하는데, 사실 내용은 우리가 이미 배운 삼각형의 합동 조건인 SSS합동, SAS합동, ASA합동을 활용한 것이기에 크게 생소하지 않다. 작도를 통한 직접 증명이 어려운 경우에는 '귀류법'을 통해 결론이 모순됨을 보여서 그 역(易)이 성립함을 증명하는 간접증명 방식으로 되어 있다.

많은 사람들이 수학책을 읽는 것을 어렵게 느낀다. 사실, 모든 내용을 완벽하게 이해하기는 어렵다. 그렇지만, 모든 것을 알려고 하기보다는 차근차근 익힌다는 생각을 해야하는 것이 수학에 좀더 친숙하게 다가가는 길이 아닐까 생각해본다.

 우리는  <논어>, <순수이성비판> 등을 한 번 읽고 내려놓지 않는다.  <원론> 역시 이처럼 여러 번 읽는다면 크게 어려운 내용은 아니라는 생각을 해본다. 문학책을 읽듯이 여러 차례 부담없이 읽는다면 '기하학적인 사고'를 읽힐 수 있다는 생각이 든다. 

다만, 그 전에 반드시 문제를 풀면서 나가겠다는 부담을 가지지 않는 것이 중요하다는 생각이 든다. 수험생이 아니라면, 모든 문제를 증명할 필요는 없지 않겠는가? 받아들일 수 있는 사항만 받아들이면서 '고대 그리스 철학자들은 이렇게 생각했구나.'하면서 친근하게 접근한다면 어느새 그들에게 동화될 수 있으리라는 생각이 든다.(고대 그리스 철학자들의 수학적 학습법이 궁금하다면 플라톤의 <메논>을 추천한다.)

그렇게 하다보면 누가 또 알겠는가. 수학에 빠져있는 자신을 발견할지.

다른 사람들은 카페에서 스마트 폰을 꺼내서 게임하는 동안, 가방에서 '컴파스'와 '자'를 꺼내서 취미로 수학문제를 푸는 자신을 발견할 수 있다면 그것도 멋진 일이라 생각한다.(쓰고나서 생각해보니, 주변에서 이상하게 볼 수도 있겠다.)

[그림2 ] 자와 컴파스 ( 사진출처 : http://smart.science.go.kr/scienceSubject/maths/view.action?menuCd=DOM_000000101001006000&subject_sid=286)

PS1. 스피노자의 <에티카>가 어려웠다면, 유클리드의 <원론>부터 훑어보는 것도 하나의 방법이라 생각된다. <에티카>는 마치 <원론>의 인문학적으로 패러디한 느낌이 기 때문에 그 차이를 알면 은근히 재밌다. <원론>의 기본구조를 빼다 박은 구조를 파악하지 못한다면, 마치 말기암환자 수술을 집도하는 의사처럼 <에티카>를 열어보자마자 덮게 될 가능성이 매우 높다.(경험담이다..ㅜㅜ)

PS2. <원론>은 수학책임에도 페이지와 법칙의 순서를 표시하는 곳 이외에는 숫자가 전혀 사용되지 않는다. 때문에 숫자알레르기가 있어서 수학책 못보시겠다는 분들은 이러한 말씀을 이 책에서는 못하실 것이다.

원주율(pi)의 역사 : 인류의 역사

π의 역사 ㅣ 경문수학산책 17
페트르 베크만 지음, 박영훈 옮김 / 경문사(경문북스) / 2002년 1월

지금도 그렇지만 대학생 때 나는 시(詩)에 대해 잘 알지 못했었다. 그런 내가 어느날 교보문고에서 본 어느 시집 제목이 상당히 인상적이었다.

<손끝으로 원을 그려봐 네가 그릴 수 있는 한 크게 그걸 뺀 만큼 널 사랑해>

한때 150만부나 팔린 원태연 시집 제목이다. 당시, 이 시집 제목을 보고 "이 사람 선수구나." 라는 생각을 했었다. 이와 같은 고백을 듣고 가슴설레지 않을 사람이 있을까.(물론 이런 표현은 가끔 써야지 자주 들으면 별로 효과도 없을 것이다.)

'세상에서 너를 가장 사랑해'라는  이 멋진 말을 수학적으로 따져보면 다음과 같이 나오지 않을까. 

한국여성의 평균 키가 162.3cm라 가정(2014년 평균)했을 때, 두 팔을 뻗었을 때의 근사치는 160cm다.  원의 정의를 고려할 경우 이 여성이 그릴 수 있는 원의 크기는 약 509.6cm수준으로 계산된다. 이 원을 제외한 세상의 크기는 무한대에 가깝다. 결국 '무한대 - 509.6cm'만큼 너를 사랑한다는 이야기가 성립하며, 수학에서 말하는 무한대의 극한을 고려하면, '무한대-509.6cm'는 무한대로 수렴한다...

* 유클리드 기하학에서 원(圓) 또는 동그라미는 평면 상의 어떤 점에서 거리가 일정한 점들의 집합으로 정의되는 평면도형이다(출처 : 위키피디아)

** 원주율(圓周率)은 원의 지름에 대한 둘레의 비율을 나타내는 수학 상수이다. 수학과 물리학의 여러 분야에 두루 쓰인다. 그리스 문자 π로 표기하고, 파이(π)라고 읽는다

결국, '네가 어떻게 해도, 난 너를 무한히 사랑해.'라는 다소 억지스럽고 무리한 수학적 해석을 해본다.  위의 전개 논리중 162.3cm에서 509.6cm으로 가는 과정, 즉 원주율(파이)의 역사를 다룬 책이 <파이의 역사 A History of pi>다.

파이의 역사에서는 원주율을 중심으로 수학의 역사를 설명한다. 원주율을 구하는 방법을 크게 기하학적인 방법, 대수학적인 방법, 확률론적인 방법으로 구분하여 각각의 역사를 기술하고 있는데 기본적인 내용과 결론을 요약하면 다음과 같다.

기하학적으로 원주율을 구하려는 노력은 아르키메데스의 방법이 가장 대표적이다. 원에 내접하는 도형의 길이를 구해면서 근사값을 산출하는 방법으로 현대적으로는 삼각함수와 소수점을 활용한 방법이다. (p80)

대수학적으로 원주율을 구하려는 방법은 미적분학과 극한의 개념을 사용하는 방법이다. 여러 방법 중 특히 라이프니츠(1646~1716)에 의해 '라이프니츠 급수'라는 방법으로 새로운 방법론이 제시된다.(p172)

원주율(pi) = 4(1-1/3+1/5-1/7+....)

그러나, 라이프니츠 급수는 원주율에 수렴하는 정도가 너무 늦었기 때문에, 뉴튼과 오일러 등 여러 수학자들에 의해 새로운 방법이 계속 발견되었다. 특히 오일러는 arctan의 방법을 사용하여 pi의 수치 계산에 종지부를 찍게 된다.(p202)

원주율(pi) = 20arctan1/7+ 8 arctan3/79

원주율이 초월수(transcendental : 무리수도 아니면서 대수 방정식의 근도 되지 않는 수)라는 사실이 1882년 린데만에 의해 밝혀지면서, 원주율 계산에 확률론적인 방법이 도입된다. 라플라스(1749~1827)에 의해 계산된 방법은 다음과 같다.

원주율(pi) = 2L/dP

바늘의 길이 L과 선분들 사이 길이 d가 주어졌을 때(일반적으로 L=d), 바늘과 선분이 만날 확률은 충분히 많은 횟수만큼 바늘을 종이 위에 던져 바늘이 선분 위에 놓이는 횟수를 기록하여 정하는 방법이다. (p213)

이러한, 라플라스의 방법은 컴퓨터의 발전과 더불어 빛을 발하는데, 대표적인 방법 중 하나가 경영분석 방법으로도 알려져 있는  '몬테카를로 방법'이다. 원주율 계산은 컴퓨터의 발전과 더불어 초월수이면서 비순환소수인 원주율(pi)의 자리수는 계속 발견되고 있다.

이 책에서는 이처럼 수학의 여러 분야에서 '원주율'이라는 주제를 어떻게 풀이하고 있는가를 설명하고 있다. 이를 통해 각 분야의 수학사(數學史)와 더불어 기본 원리에 대해서도 알려주고 있다. 또한, 유클리드의 <원론>에 관한 설명부터, 제논의 역설(아킬레스와 거북이의 경주)이 역설이 아닌 이유에 이르기까지 여러 수학 분야에 대한 이야기를 다루기 때문에 흥미있게 읽을 수 있는 책이다.

유클리드의 <원론>에서 5가지 공리에 대한 이야기를 하면서 가장 문제가 되는 5번째 공리없이도 유클리드가 증명한 내용은 성립한다. 때문에, 반드시 5번째 공리가 성립할 필요가 없으며, 오히려 5번째 공리의 붕괴를 통해 '비(非)유클리드 기하학'이 성립되는 과정을 흥미롭게 설명한다. (p62)

거북이가 아킬레스보다 10미터 앞에서 출발하는 경주에서 아킬레스가 10미터를 가는 동안 거북이는 1미터를 가고, 다시 아킬레스가 1미터 가는 동안 거북이는 1/10미터를 가는 과정에서 결국 아킬레스는 영원히 거북이를 잡을 수가 없다는 제논의 역설에 대한 본서의 설명은 다음과 같다.

'여기에서 걸림돌은 그리스인들이 유한 값에 이르는 무한개의 합을 생각할 수 없었다는 것이다. (p56)'

<파이의 역사>를 읽으면서 기하학과 대수학이 다루는 대상이 다를지라도, 비순환소수인 원주율(pi)을 산출하는 방법은 동일하다는 것을 알 수 있었다. 그것은 일종의 '오류법'으로 파이(pi)로 다가가기 위한 포기하지 않는 노력이라 생각된다. 수작업으로 하기에 고통스러웠던 계산과정이었지만, 포기하지 않는 노력은 결국 컴퓨터의 발전을 통해 그 빛을 보게 되었다는 생각이 든다. (2010년 현재 구한 pi자리수는 2조 7천억 자리라고 한다.)

그러한 의미에서  원주율(pi)를 구하는 과정은 인간의 역사의 대표적 단면이라는 생각을 하게 된다.

PS. <손끝으로 원을 그려봐 네가 그릴 수 있는 한 크게 그걸 뺀 만큼 널 사랑해>에서 화자(話者)의 의도를 청자(聽者)가 안다면, 그 감동의 크기가 줄어들 것이라는 생각이 든다. 이 상황을 소비자의 완전정보하에서의 상황과 불완전정보의 상황과 연계시켜서 생각해보는 것도 재밌을 것 같다.^^:  

오전에 빵을 사고 집으로 왔습니다. 차를 주차하고 ...

오전에 빵을 사고 집으로 왔습니다.

차를 주차하고 집으로 들어가는 길 배수로에 낯선 것이 보여 보니, 고양이가 끼어 있었습니다. 놀라서 보니 이미 몸이 경직된 채 죽어있었습니다..

요새 뱀이 많이 나와 뱀에 물렸는지 상당히 경직되어 있었습니다. 아니면 나이가 많아 죽었는지도 모르겠네요. 낯선 녀석은 아니어서 곰곰히 생각해보니 가끔 차 밑에서 나와 저를 놀라게 했던 녀석입니다.

며칠전 고양이 소리가 밤에 들렸는데, 이 고양이 소리였던 것 같습니다.. 혹시 배수로에 끼어 살려달라는 애절함이 담긴 울음은 아니었는지 미안한 마음이 드네요..

아내와 상의해서 딸과 함께 앞쪽 작은 산에 묻어주었습니다. 딸아이는 고양이가 추워 웅크리고 잠을 자고 있다네요.
아내는 할머니 고양이가 추워하니 흙이불을 덮어주자고 말합니다.

아내는 신문지로 염을 한 후 고양이의 눈을 감겨 주고 같이 올라갔습니다. 나는 그 사이 이 군 생활이후 거의 처음으로 삽질을 했습니다. 그렇게 작은 고양이 무덤이 생겼습니다.

오늘 이렇게 딸아이에게 ｀죽음｀을 보여 주었습니다. 아이가 오늘 본 것을 어떻게 받아들일지는 모르겠습니다. 그래도 ｀헤어짐｀에 대해 작은 기억으로 남을 것 같습니다. 아내와는 이 부분에 대해 이야기했습니다. ｀죽음｀을 보여줘도 좋은지에 대해.

｀죽음｀ 이라는 문제는 성인이 된 제게도 무거운 문제입니다. 마음이 가볍지는 않네요. 다만, 녀석의 눈이 감겼으니 조금은 편안해졌으리라는 생각을 해봅니다.

내일부터 일주일간 제주도 출장입니다. 7시30분까지 목포항까지 가려니 새벽 2시에 나가네요 ㅋ 일정이 촉박하지만 시간이 되면 전에 말씀드린 ｀제주 4.3｀ 정리해 볼까합니다. 즐거운 오후 되세요^^